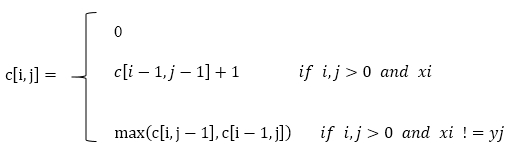經典動態規劃問題總結
動態規劃引入
首先我們以一個最基本的例子來分析——菲波那切數列。
我們都知道,菲波那切數列的遞推公式f(n) = f(n-1)+f(n-2) (這裡我就說明一般情況,不列舉邊界條件了),很簡單,如果我們用遞迴的方法來求解f(n),兩三行程式碼就出來了。那麼我們深入分析一下這樣有什麼問題?
f(2) = f(1) + f(0);
f(3) = f(2) + f(1);
f(4) = f(3) + f(2);
f(5) = f(4) + f(3);
......
計算一個f(5)我們需要計算一個f(4)和一個f(3),而一個f(4)又需要一個f(3)和一個f(2),這其中就有了一個重複的f(3),那麼在繼續往下推導,會發現有越來越多的重複。當我們在計算機中計算f(40)並輸出時,我們會發現已經有相當長時間的延時了,為什麼?因為這樣的遞迴重複計算太多了,導致整個演算法效率非常低。
由於上述過程存在著大量的重複計算,我們可以用一個數組儲存所有已經計算過的項,這樣便可以達到用空間換時間的目的,在這種情況下,時間複雜度為O(N),而空間複雜度也為O(N)。事實上,我們所述的這種演算法就是利用了動態規劃的思想。
動態規劃演算法的思想與分治法類似,也是通過組合子問題的解而解決整個問題。其基本思路是利用一個表來記錄所有已解的子問題的答案,不管該子問題以後是否被用到,只要它被計算過,就將結果填入表中,這樣就可以避免重複計算問題。
動態規劃演算法的設計可以分為如下幾個步驟:
1)描述最優解的結構;
2)遞迴定義最優解的值;
3)按自底向上的方式計算最優解的值;
4)由計算出的結果構造一個最優解;
其中第1~3步構成問題的動態規劃解的基礎。
適合動態規劃方法的最優化問題的兩個要素:最優子結構,重疊子問題。
例1:求用1*2的瓷磚覆蓋2*M的地板有幾種方式?
分析:假設所求問題的解為F(M),有下面兩種情況:
當第一塊瓷磚豎著放的時候,問題轉換成求用1*2的瓷磚覆蓋剩下的2*(M-1)的方式,即F(M-1)。
當第一塊瓷磚橫著放的時候,則必有另一塊瓷磚橫著放在其下面,問題轉換成求用1*2的瓷磚覆蓋 剩下的2*(M-2)的方式,即F(M-2)。
在求F(M-1)和F(M-2)時,由於第一列地板的覆蓋方式已經不同,故F(M-1)種覆蓋方式和F(M-2)中覆蓋方式沒有重疊,故:
F(M) = F(M-1)+F(M-2)
其中,F(1) = 1,F(2) = 2。可見我們能夠將問題規模縮小。
仔細看遞推式,其實就和菲波那切數列是一樣的,既然這樣,我們就不要用上面的遞迴方式進行求解F(M)了,而是用動態規劃的方式,建立一個表格,儲存每一步驟的F(i).
//...
int a[100];
int func(int M){}
a[1] = 1;
a[2] = 2;
for(int i = 3; i <= M; ++i)
a[i] = a[i-1] + a[i-2];
return a[M];
}
//...例2:LCS(最長公共子序列問題)
注:LCS問題不要求所求得的字元在所給的字串中是連續的。
分析:假設X={x1,x2,...,xm}和Y={y1,y2,...,yn}的一個最長公共子序列為Z={z1,z2,...,zk},
1)若x(m) = y(n),則必然有z(k) = x(m) = y(n),且Z(k-1)是X(m-1)和Y(n-1)的最長公共子序列;
2)若x(m) != y(n)且z(k) != x(m),則Z是X(m-1)和Y的最長公共子序列;
3)若x(m) != y(n) 且z(k) != y(n),則Z是X和Y(n-1)的最長公共子序列;
也就是說,
當x(m) = y(n)時,LCS(X(m),Y(n)) = LCS(X(m-1),Y(n-1)) + 1;
當x(m) != y(n)時,LCS(X(m),Y(n)) = max{LCS(X(m-1),Y(n)), LCS(X(m),Y(n-1))};
若用一個二維表格c來儲存LCS,則c[i][j]表示X和Y長度分別為i和j時的LCS,顯然,當X或Y為空時,LCS為0.
下面給出動態規劃演算法的程式碼:
/* 動態規劃:最長公共子序列問題LCS */
const int INF = 99999;
int c[100][100];
int LCS_Memo(string A, string B, int i, int j){
if(c[i][j] < INF)
return c[i][j];
if(i == 0 || j == 0)
c[i][j] = 0;
else if(A[i-1] == B[j-1])
c[i][j] = c[i-1][j-1] + 1;
else{
int p = LCS_Memo(A, B, i-1, j);
int q = LCS_Memo(A, B, i, j-1);
if(p >= q)
c[i][j] = p;
else
c[i][j] = q;
}
return c[i][j];
}
int LCS_Length(string A, string B){
int m = A.length();
int n = B.length();
memset(c, INF, sizeof(c));
return LCS_Memo(A, B, m, n);
}//dp[i][j]存放的是長度分別為i、j的字串A、B的LCS
int LCS(string A, string B, int m, int n){
int dp[300][300];
memset(dp, 0, sizeof(dp));
for(int i = 1; i <= m; ++i){
for(int j = 1; j <= n; ++j){
if(A[i-1] == B[j-1])
dp[i][j] = dp[i-1][j-1] + 1;
else
dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
}
}
return dp[m][n];
}分析:這裡以行n,列cap建立二維表格dp[n+1][cap+1],其中dp[i][j]表示重量不超過j時的最大價值。那麼這裡就有兩種情況:
1)選擇第i件物品,則前i-1件物品的重量不能超過j-w[i];
2)不選擇第i件物品,則前i-1件物品的重量不能超過j;
即dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
int getMaxValue(vector<int> w, vector<int> v, int n, int cap){
int dp[n+1][cap+1];
for(int i = 0; i <= n; ++i)
dp[i][0] = 0;
for(int j = 0; j <= cap; ++j)
dp[0][j] = 0;
for(int i = 1; i <= n; ++i){
for(int j = 1;j <= cap; ++j){
if(j >= w[i-1])
dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i-1]]+v[i-1]);
else
dp[i][j] = dp[i-1][j];
}
}
}