本文介紹了K-means聚類演算法，並註釋了部分matlab實現的原始碼。

K-means演算法

K-means演算法是一種硬聚類演算法，根據資料到聚類中心的某種距離來作為判別該資料所屬類別。K-means演算法以距離作為相似度測度。

假設將物件資料集分為個不同的類，k均值聚類演算法步驟如下：

Step1：隨機從物件集中抽取個物件作為初始聚類中心；

Step2：對於所有的物件，分別計算其到各個聚類中的歐氏距離，相互比較後將其歸屬於距離最小的那一類；

Step3：根據step2得到的初始分類，對每個類別計算均值用來更新聚類中心；

Step4：根據新的聚類中心，重複進行step2和step3,直至滿足演算法終止條件。

K-means演算法是基於劃分的思想，因此演算法易於理解且實現方法簡單易行，但需要人工選擇初始的聚類數目即演算法是帶引數的。類的數目確定往往非常複雜和具有不確定性，因此需要專業的知識和行業經驗才能較好的確定。而且因為初始聚類中心的選擇是隨機的，因此會造成部分初始聚類中心相似或者處於資料邊緣，造成演算法的迭代次數明顯增加，甚至會因為個別資料而造成聚類失敗的現象。

其流程圖大致如下：

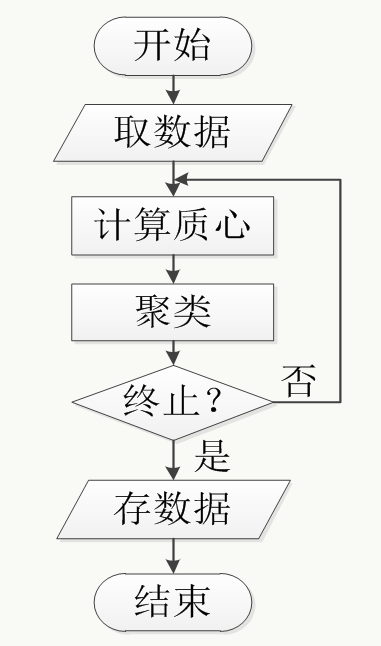
matlab原始碼

function varargout = kmeans(X, k, varargin)
%K均值聚類.
%   IDX = KMEANS(X, K) 分割X[N P]的資料矩陣中的樣本為K個類，是一種最小化類內點到中心距離和的總和的分割。 
%   矩陣X中的行對應的是資料樣本，列對應的是變數。
%   提示: 當X是一個向量，本函式會忽略它的方向，將其當作一個[N 1]的資料矩陣。 
%   KMEANS 函式返回一個代表各個資料樣本所屬類別索引的[N 1]維向量，函式預設使用平方的歐氏距離。 
%   KMEANS 將NaNs當作丟失的資料並且忽略X中任何包含NaNs的行 
%   
%
%   [IDX, C] = KMEANS(X, K) 返回一個包含K個聚類中心的[K P]維的矩陣C.
%
%   [IDX, C, SUMD] = KMEANS(X, K) 返回一個類間點到聚類中心距離和的[K 1]維向量SUMD。
%
%   [IDX, C, SUMD, D] = KMEANS(X, K) 返回一個每個點到任一聚類中心距離的[N K]維矩陣D。
%
%   [ ... ] = KMEANS(..., 'PARAM1',val1, 'PARAM2',val2, ...) 指定了可選引數對（引數名/引數值）來控制演算法的迭代。
%   引數如下：
%
%   'Distance' - 距離測度,  P維空間,  KMEANS演算法需要最小化的值
%         可以選擇:
%          'sqeuclidean'  - 平方的歐氏距離 (預設)
%          'cityblock'    - 曼哈頓距離，各維度差異的絕對值之和。
%          'cosine'       - 1減去兩個樣本（當作向量）夾角的餘弦值 
%          'correlation'  - 1減去兩個樣本(當作值的序列)的相關係數 
%                           
%          'hamming'      - 漢明距離，二進位制資料相匹配位置的不同位元百分比。 
%
%   'Start' - 選擇初始聚類中心的方法,有時候也稱作種子。
%         可以選擇:
%          'plus'    - 預設值。 利用k-means++演算法從X中選擇K個觀測值：從X中隨機的選取第一個聚類中心；之後的
%                      聚類中心以一定的概率從剩餘的樣本中根據其到最近的聚類中心的比例來隨機的選取。  
%          'sample'  - 隨機的從X中選取K個觀測值。
%          'uniform' - 根據X的取值範圍均勻的隨機選取K個樣本，對漢明距離不適用。
%          'cluster' - 隨機的利用X中10%的樣本進行一個預聚類的階段，預聚類階段的初始聚類中心選取採用‘sample’。 
%           matrix   - 一個初始聚類中心的[K P]維矩陣。此時,你可以用[]代替K，演算法會自動的根據矩陣的第一個維度推算K值。
%                      你也可以使用3D陣列，暗含著第三維為引數'Replicates'的值。
%
%   'Replicates' - 重複聚類的次數,預設為1。 每次都會有一個新的初始聚類中心。 
%
%   'EmptyAction' - 發生空類時的處理措施。
%         可以選擇:
%          'singleton' - 預設方法。利用據該中心最遠的一個觀測值建立一個新的類。
%          'error'     - 將產生空類作為一個錯誤(error)。
%          'drop'      - 移除空類並將對應的C和D中的值設定為NaN。
%         
%
%   'Options' - 迭代演算法最小化擬合準則(？)的選項，通過STATSET建立。 Choices of STATSET
%          STATSET引數可以選擇:
%
%          'Display'  - 顯示輸出的哪一階段的值，可以為 'off'(預設），‘iter’和‘final’;
%          'MaxIter'  - 最大的迭代次數，預設值為100。
%
%          'UseParallel'  - 在滿足條件下，如果為真則開啟平行計算否則使用序列模式。預設使用序列模式。  
%          'UseSubstreams'  - 預設不使用。
%          'Streams'  - 這些區域指明是否執行並行的多個‘Start’值和當產生初始聚類中心時如何使用隨機數值，
%                       更詳細的參考 PARALLELSTATS。 
%                       提示: 如果 'UseParallel'為TRUE且 'UseSubstreams'為FALSE,
%                       那麼'Streams'的長度必須等於KMEANS使用的workers的數目。 
%                       如果打開了並行池，那麼它的大小和並行池一樣。如果沒有開啟並行池，
%                       那麼MATLAB可能會自動的開啟(這取決於你的安裝設定)。為了得到更好的結果，
%                       建議運用PARPOOL命令建立並行池的優先順序以便當'UseParallel'為TRUE時執行演算法。
%
%         'OnlinePhase' - 標誌位，表示KMEANS是否除了執行一個"batch update"階段還需一個"on-line
%                         update"階段 。on-line階段在大資料量時耗時很多。預設為‘off’。
%
%   示例:
%
%       X = [randn(20,2)+ones(20,2); randn(20,2)-ones(20,2)];
%       opts = statset('Display','final');
%       [cidx, ctrs] = kmeans(X, 2, 'Distance','city', ...
%                             'Replicates',5, 'Options',opts);
%       plot(X(cidx==1,1),X(cidx==1,2),'r.', ...
%            X(cidx==2,1),X(cidx==2,2),'b.', ctrs(:,1),ctrs(:,2),'kx');
%
%   也可以參考LINKAGE, CLUSTERDATA, SILHOUETTE。

%   KMEANS 運用兩階段迭代演算法來最小化K個類中樣本到中心的距離和。 
%   第一階段利用文獻中經常描述的"batch" 更新, 其中每次迭代中都一
%   次性地將樣本分配到最近的聚類中心，然後更新聚類中心。這一階段
%   偶爾(特別實在小樣本的時候)會陷入區域性最優。因此，"batch"階段可
%   以考慮為第二階段提供一個快速且可能為近似解的初始聚類中心。第二
%   階段利用文獻中常提及的"on-line"更新， 其中。如果能夠減小距離
%   的總和那麼其中的樣本點都是單獨地重新分配且每次分配後都重新計算
%   聚類中心。第二階段中的每次迭代都會遍歷所有的點，但是on-line階段會收
%   斂到一個區域性最小值。尋找全域性最優的問題一般只能通過詳細(幸運)地選擇初始
%   聚類中心，但是使用重複多次的使用隨機初始聚類中心中的典型結果是一個全域性最小。
%
%  參考文獻:
%
%   [1] Seber, G.A.F. (1984) Multivariate Observations, Wiley, New York.
%   [2] Spath, H. (1985) Cluster Dissection and Analysis: Theory, FORTRAN
%       Programs, Examples, translated by J. Goldschmidt, Halsted Press,
%       New York.

%判斷輸入變數是否少於兩個
if nargin < 2 
    error(message('stats:kmeans:TooFewInputs'));
end
%判斷X是否是實數矩陣；
if ~isreal(X) 
    error(message('stats:kmeans:ComplexData'));
end
%查詢是否有NaN資料，有的話就刪除，更新X矩陣；
wasnan = any(isnan(X),2);
hadNaNs = any(wasnan);
if hadNaNs
    warning(message('stats:kmeans:MissingDataRemoved'));
    X = X(~wasnan,:);
end

% 獲取X矩陣的維數
[n, p] = size(X);
%引數名與預設引數值設定
pnames = {   'distance'  'start' 'replicates' 'emptyaction' 'onlinephase' 'options' 'maxiter' 'display'};
dflts =  {'sqeuclidean' 'plus'          []  'singleton'         'off'        []        []        []};
[distance,start,reps,emptyact,online,options,maxit,display] ...
    = internal.stats.parseArgs(pnames, dflts, varargin{:});

distNames = {'sqeuclidean','cityblock','cosine','correlation','hamming'};
distance = internal.stats.getParamVal(distance,distNames,'''Distance''');

switch distance
    case 'cosine'
        Xnorm = sqrt(sum(X.^2, 2));%模長
        if any(min(Xnorm) <= eps(max(Xnorm)))
            error(message('stats:kmeans:ZeroDataForCos'));
        end
        X =  bsxfun(@rdivide,X,Xnorm);%標準化
    case 'correlation'
        X = bsxfun(@minus, X, mean(X,2));
        Xnorm = sqrt(sum(X.^2, 2));
        if any(min(Xnorm) <= eps(max(Xnorm)))
            error(message('stats:kmeans:ConstantDataForCorr'));
        end
        X =  bsxfun(@rdivide,X,Xnorm);
     case 'hamming'
       if  ~all( X(:) ==0 | X(:)==1)
            error(message('stats:kmeans:NonbinaryDataForHamm'));
      end
end

Xmins = [];
Xmaxs = [];
CC = [];
if ischar(start)
    startNames = {'uniform','sample','cluster','plus','kmeans++'};
    j = find(strncmpi(start,startNames,length(start)));
    if length(j) > 1
        error(message('stats:kmeans:AmbiguousStart', start));
    elseif isempty(j)
        error(message('stats:kmeans:UnknownStart', start));
    elseif isempty(k)
        error(message('stats:kmeans:MissingK'));
    end
    start = startNames{j};
    if strcmp(start, 'uniform')
        if strcmp(distance, 'hamming')
            error(message('stats:kmeans:UniformStartForHamm'));
        end
        Xmins = min(X,[],1);%求每一列的最小值
        Xmaxs = max(X,[],1);%求每一列的最大值
    end
elseif isnumeric(start) %如果初始中心是數值型別(numeric)
    CC = start;
    start = 'numeric';
    if isempty(k)
        k = size(CC,1);%如果K為空通過數值的初始聚類中心獲取K值
    elseif k ~= size(CC,1);%檢測初始聚類中心行是否合法
        error(message('stats:kmeans:StartBadRowSize'));
    elseif size(CC,2) ~= p %檢測初始聚類中心列是否合法
        error(message('stats:kmeans:StartBadColumnSize'));
    end
    if isempty(reps) 
        reps = size(CC,3);%如果重複次數引數為空，檢測初始聚類中心的第三維獲取
    elseif reps ~= size(CC,3);
        error(message('stats:kmeans:StartBadThirdDimSize'));
    end
    
    % Need to center explicit starting points for 'correlation'. (Re)normalization
    % for 'cosine'/'correlation' is done at each iteration.
    if isequal(distance, 'correlation')
          CC = bsxfun(@minus, CC, mean(CC,2));%如果距離測度為相關性需要中心化資料
    end
else
    error(message('stats:kmeans:InvalidStart'));
end

emptyactNames = {'error','drop','singleton'};
emptyact = internal.stats.getParamVal(emptyact,emptyactNames,'''EmptyAction''');

[~,online] = internal.stats.getParamVal(online,{'on','off'},'''OnlinePhase''');
online = (online==1);

% 'maxiter' and 'display' are grandfathered as separate param name/value pairs
if ~isempty(display)
    options = statset(options,'Display',display);
end
if ~isempty(maxit)
    options = statset(options,'MaxIter',maxit);
end

options = statset(statset('kmeans'), options);
display = find(strncmpi(options.Display, {'off','notify','final','iter'},...
    length(options.Display))) - 1;
maxit = options.MaxIter;%確定最大迭代次數

if ~(isscalar(k) && isnumeric(k) && isreal(k) && k > 0 && (round(k)==k))
    error(message('stats:kmeans:InvalidK'));
    % elseif k == 1
    % this special case works automatically
elseif n < k
    error(message('stats:kmeans:TooManyClusters'));
end

% Assume one replicate 檢測重複次數的值
if isempty(reps)
    reps = 1;
elseif ~internal.stats.isScalarInt(reps,1)
    error(message('stats:kmeans:BadReps'));
end

[useParallel, RNGscheme, poolsz] = ...
    internal.stats.parallel.processParallelAndStreamOptions(options,true);

usePool = useParallel && poolsz>0;%檢測是否使用並行池

% Prepare for in-progress
if display > 1 % 'iter' or 'final'
    if usePool
        % If we are running on a parallel pool, each worker will generate
        % a separate periodic report.  Before starting the loop, we
        % seed the parallel pool so that each worker will have an
        % identifying label (eg, index) for its report.
        internal.stats.parallel.distributeToPool( ...
            'workerID', num2cell(1:poolsz) );
        
        % Periodic reports behave differently in parallel than they do
        % in serial computation (which is the baseline).
        % We advise the user of the difference.
        
        if display == 3 % 'iter' only
            warning(message('stats:kmeans:displayParallel2'));
            fprintf('    worker\t  iter\t phase\t     num\t         sum\n' );
        end
    else
        if useParallel
            warning(message('stats:kmeans:displayParallel'));
        end
        if display == 3 % 'iter' only
            fprintf('  iter\t phase\t     num\t         sum\n');
        end
    end
end

if issparse(X) || ~isfloat(X) || strcmp(distance,'cityblock') || ...
        strcmp(distance,'hamming')
    [varargout{1:nargout}] = kmeans2(X,k, distance, emptyact,reps,start,...
        Xmins,Xmaxs,CC,online,display, maxit,useParallel, RNGscheme,usePool,...
        wasnan,hadNaNs,varargin{:});
    return;
end

emptyErrCnt = 0;

% Define the function that will perform one iteration of the
% loop inside smartFor
loopbody = @loopBody;%定義迴圈體函式

% Initialize nested variables so they will not appear to be functions here
%初始化迴圈巢狀變數
totsumD = 0;
iter = 0;

%將資料轉置
X = X'; 
Xmins = Xmins';
Xmaxs = Xmaxs';

% 執行KMEANS多次(reps)在各自的工作區上.
ClusterBest = internal.stats.parallel.smartForReduce(...
    reps, loopbody, useParallel, RNGscheme, 'argmin');

% 選出最優解
varargout{1} = ClusterBest{5};%最優解的索引idx
varargout{2} = ClusterBest{6}';%最優解的聚類中心C
varargout{3} = ClusterBest{3}; %最優解的類內距離和sumD
totsumDbest = ClusterBest{1};%最優解的所有類內距離和的總和

if nargout > 3
    varargout{4} = ClusterBest{7}; %最優解的點到任意聚類中心的距離
end

if display > 1 % 'final' or 'iter'
    fprintf('%s\n',getString(message('stats:kmeans:FinalSumOfDistances',sprintf('%g',totsumDbest))));
end
 
if hadNaNs
    varargout{1} = statinsertnan(wasnan, varargout{1});% idxbest 
    if nargout > 3
        varargout{4} = statinsertnan(wasnan, varargout{4}); %Dbest
    end
end

    function cellout = loopBody(rep,S)%迴圈體函式
        
        if isempty(S)
            S = RandStream.getGlobalStream;
        end
        
        if display > 1 % 'iter'
            if usePool
                dispfmt = '%8d\t%6d\t%6d\t%8d\t%12g\n';
                labindx = internal.stats.parallel.workerGetValue('workerID');
            else
                dispfmt = '%6d\t%6d\t%8d\t%12g\n';
            end
        end

        %定義元胞陣列
        cellout = cell(7,1);  % cellout{1}類間距離總和
                              % cellout{2}重複次數
                              % cellout{3}類內距離總和
                              % cellout{4}迭代次數
                              % cellout{5}索引
                              % cellout{6}聚類中心
                              % cellout{7}距離
        
        % Populating total sum of distances to Inf. This is used in the
        % reduce operation if update fails due to empty cluster.
        cellout{1} = Inf;%賦值
        cellout{2} = rep;

        %初始化聚類中心
        switch start
            case 'uniform'
                %C = Xmins(:,ones(1,k)) + rand(S,[p,k]).*(Xmaxs(:,ones(1,k))-Xmins(:,ones(1,k)));
                C = Xmins(:,ones(1,k)) + rand(S,[k,p])'.*(Xmaxs(:,ones(1,k))-Xmins(:,ones(1,k)));
                % For 'cosine' and 'correlation', these are uniform inside a subset
                % of the unit hypersphere.仍需要為'correlation'進行中心化.  
                %  'cosine'/'correlation'的正交化在每次迭代中完成

                if isequal(distance, 'correlation')
                    C = bsxfun(@minus, C, mean(C,1));
                end
                if isa(X,'single')
                    C = single(C);
                end
            case 'sample'
                C = X(:,randsample(S,n,k));
            case 'cluster'
                Xsubset = X(:,randsample(S,n,floor(.1*n)));
                % Turn display off for the initialization
                optIndex = find(strcmpi('options',varargin));
                if isempty(optIndex)
                    opts = statset('Display','off');
                    varargin = [varargin,'options',opts];
                else
                    varargin{optIndex+1}.Display = 'off';
                end
                [~, C] = kmeans(Xsubset', k, varargin{:}, 'start','sample', 'replicates',1);
                C = C';
            case 'numeric'
                C = CC(:,:,rep)';
                if isa(X,'single')
                    C = single(C);
                end
            case {'plus','kmeans++'}
                % Select the first seed by sampling uniformly at random
                index = zeros(1,k);
                [C(:,1), index(1)] = datasample(S,X,1,2);
                minDist = inf(n,1);
           
                % Select the rest of the seeds by a probabilistic model
               for ii = 2:k                    
                    minDist = min(minDist,distfun(X,C(:,ii-1),distance));
                    denominator = sum(minDist);
                    if denominator==0 || isinf(denominator) || isnan(denominator)
                        C(:,ii:k) = datasample(S,X,k-ii+1,2,'Replace',false);
                        break;
                    end
                    sampleProbability = minDist/denominator;
                    [C(:,ii), index(ii)] = datasample(S,X,1,2,'Replace',false,...
                        'Weights',sampleProbability);        
                end
        end
        if ~isfloat(C)      % X may be logical
            C = double(C);
        end
        
        % 計算點到聚類中心的距離和歸屬到各個類別
        D = distfun(X, C, distance, 0, rep, reps);%計算點到箇中心的距離
        [d, idx] = min(D, [], 2);%根據最短距離歸屬到各個類
        m = accumarray(idx,1,[k,1])';%計算各個類中樣本的個數
        
        try % catch空類錯誤並轉移到下一個重複次
            
            %開始第一階段:批分配
            converged = batchUpdate();
            
            % 開始第二階段：單個分配
            if online
                converged = onlineUpdate();
            end
            
            
            if display == 2 % 'final'
                fprintf('%s\n',getString(message('stats:kmeans:IterationsSumOfDistances',rep,iter,sprintf('%g',totsumD) )));
            end
            
            if ~converged
                if reps==1
                    warning(message('stats:kmeans:FailedToConverge', maxit));
                else
                    warning(message('stats:kmeans:FailedToConvergeRep', maxit, rep));
                end
            end
            
            % 計算類內距離和
            nonempties = find(m>0);%判斷沒有空類，生成非空類的線性目錄
            D(:,nonempties) = distfun(X, C(:,nonempties), distance, iter, rep, reps);
            d = D((idx-1)*n + (1:n)');
            sumD = accumarray(idx,d,[k,1]);% 計算類內距離和
            totsumD = sum(sumD(nonempties));% 計算所有類內距離和的總和
            
            % 儲存目前最好的解
            cellout = {totsumD,rep,sumD,iter,idx,C,D}';
           
            % 如果在重複執行中發生空類現象,進行捕獲並警告，然後繼續下一次重複執行，
            %  只有在所有的重複執行失敗才會ERROR，再次引發另一種ERROR。
        catch ME
            if reps == 1 || (~isequal(ME.identifier,'stats:kmeans:EmptyCluster')  && ...
                         ~isequal(ME.identifier,'stats:kmeans:EmptyClusterRep'))
                rethrow(ME);
            else
                emptyErrCnt = emptyErrCnt + 1;
                warning(message('stats:kmeans:EmptyClusterInBatchUpdate', rep, iter));
                if emptyErrCnt == reps
                    error(message('stats:kmeans:EmptyClusterAllReps'));
                end
            end
        end % catch
        
        %------------------------------------------------------------------
        
        function converged = batchUpdate()
            
            % 遍歷每個點，更新每個類
            moved = 1:n;
            changed = 1:k;
            previdx = zeros(n,1);
            prevtotsumD = Inf;
            
            %
            % 開始第一階段
            %
            
            iter = 0;
            converged = false;
            while true
                iter = iter + 1;
                
                % 更新新的聚類中心和數目以及每個樣本到新聚類中心的距離 
                [C(:,changed), m(changed)] = gcentroids(X, idx, changed, distance);
                D(:,changed) = distfun(X, C(:,changed), distance, iter, rep, reps);
                
                %處理空類
                empties = changed(m(changed) == 0);
                if ~isempty(empties)
                    if strcmp(emptyact,'error')
                        if reps==1
                            error(message('stats:kmeans:EmptyCluster', iter));
                        else
                            error(message('stats:kmeans:EmptyClusterRep', iter, rep));
                        end
                    end
                    switch emptyact
                        case 'drop'
                            if reps==1
                                warning(message('stats:kmeans:EmptyCluster', iter));
                            else
                                warning(message('stats:kmeans:EmptyClusterRep', iter, rep));
                            end
                            % Remove the empty cluster from any further processing
                            D(:,empties) = NaN;
                            changed = changed(m(changed) > 0);
                        case 'singleton'
                            for i = empties
                                d = D((idx-1)*n + (1:n)'); % use newly updated distances
                                
                                % 選取一個距離當前類最遠的樣本作為一個新的類
                                [~, lonely] = max(d);
                                from = idx(lonely); % taking from this cluster
                                if m(from) < 2
                                    % In the very unusual event that the cluster had only
                                    % one member, pick any other non-singleton point.
                                    from = find(m>1,1,'first');
                                    lonely = find(idx==from,1,'first');
                                end
                                C(:,i) = X(:,lonely);
                                m(i) = 1;
                                idx(lonely) = i;
                                D(:,i) = distfun(X, C(:,i), distance, iter, rep, reps);
                                
                                % Update clusters from which points are taken
                                [C(:,from), m(from)] = gcentroids(X, idx, from, distance);
                                D(:,from) = distfun(X, C(:,from), distance, iter, rep, reps);
                                changed = unique([changed from]);
                            end
                    end
                end
                
                % 在當前配置下計算總距離
                totsumD = sum(D((idx-1)*n + (1:n)'));
                % 迴圈測試: 如果目標為減少,返回出去
                % 最後一步，之後進行單個更新階段
                if prevtotsumD <= totsumD
                    idx = previdx;
                    [C(:,changed), m(changed)] = gcentroids(X, idx, changed, distance);
                    iter = iter - 1;
                    break;
                end
                if display > 2 % 'iter'
                    if usePool
                        fprintf(dispfmt,labindx,iter,1,length(moved),totsumD);
                    else
                        fprintf(dispfmt,iter,1,length(moved),totsumD);
                    end
                end
                if iter >= maxit
                    break;
                end
                
                %對每個點根據就近原則歸屬到各自的類 
                previdx = idx;
                prevtotsumD = totsumD;
                [d, nidx] = min(D, [], 2);
                
                % 決定哪個樣本點移動
                moved = find(nidx ~= previdx);
                if ~isempty(moved)
                    % Resolve ties in favor of not moving
                    moved = moved(D((previdx(moved)-1)*n + moved) > d(moved));
                end
                if isempty(moved)
                    converged = true;
                    break;
                end
                idx(moved) = nidx(moved);
                
                % 尋找得到或者失去樣本點的類
                changed = unique([idx(moved); previdx(moved)])';
                
            end % phase one
            
        end % nested function
        
        %------------------------------------------------------------------
        
        function converged = onlineUpdate()
                       
            %
            % 第二階段開始: 單個分配
            %
            changed = find(m > 0);
            lastmoved = 0;
            nummoved = 0;
            iter1 = iter;
            converged = false;
            Del = NaN(n,k); % 重新分配的準則
            while iter < maxit
                %計算每個樣本點到各個類的距離以及因每個類中新增或者移除樣本點引起的誤差和的變化
                %沒有發生變化的類並不用更新。僅含單個樣本點的類是總距離計算中的特殊情況。
                %移除它們僅有的樣本點並不是最好的選擇，根據分配準則最好保證它們能夠得到保留， 
                %令人高興地是，對於這種情況我們自動的使用Del(i,idx(i)) == 0。 
                switch distance
                    case 'sqeuclidean'
                        for i = changed
                            mbrs = (idx == i)';
                            sgn = 1 - 2*mbrs; % -1 for members, 1 for nonmembers
                            if m(i) == 1
                                sgn(mbrs) = 0; % prevent divide-by-zero for singleton mbrs
                            end
                          Del(:,i) = (m(i) ./ (m(i) + sgn)) .* sum((bsxfun(@minus, X, C(:,i))).^2, 1);
                        end
                      case {'cosine','correlation'}
                        % The points are normalized, centroids are not, so normalize them
                        normC = sqrt(sum(C.^2, 1));
                        if any(normC < eps(class(normC))) % small relative to unit-length data points
                            if reps==1
                                error(message('stats:kmeans:ZeroCentroid', iter));
                            else
                                error(message('stats:kmeans:ZeroCentroidRep', iter, rep));
                            end
                            
                        end
                        % This can be done without a loop, but the loop saves memory allocations
                        for i = changed
                            XCi =  C(:,i)'*X;
                            mbrs = (idx == i)';
                            sgn = 1 - 2*mbrs; % -1 for members, 1 for nonmembers
                            Del(:,i) = 1 + sgn .*...
                                (m(i).*normC(i) - sqrt((m(i).*normC(i)).^2 + 2.*sgn.*m(i).*XCi + 1));
                        end
                end
                
                % 對於任意一個樣本點，確定可能是最好的移動方式。然後選擇其中的一個進行移動
                previdx = idx;
                prevtotsumD = totsumD;
                [minDel, nidx] = min(Del, [], 2);
                moved = find(previdx ~= nidx);
                moved(m(previdx(moved))==1)=[];
                if ~isempty(moved)
                    % Resolve ties in favor of not moving
                    moved = moved(Del((previdx(moved)-1)*n + moved) > minDel(moved));
                end
                if isempty(moved)
                    % Count an iteration if phase 2 did nothing at all, or if we're
                    % in the middle of a pass through all the points
                    if (iter == iter1) || nummoved > 0
                        iter = iter + 1;
                        if display > 2 % 'iter'
                            if usePool
                                fprintf(dispfmt,labindx,iter,2,length(moved),totsumD);
                            else
                                fprintf(dispfmt,iter,2,length(moved),totsumD);
                            end
                        end
                    end
                    converged = true;
                    break;
                end
                
                % Pick the next move in cyclic order
                %迴圈地選擇下一次的移動
                moved = mod(min(mod(moved - lastmoved - 1, n) + lastmoved), n) + 1;
                
                % 遍歷完所有的樣本點，則完成一次迭代
                if moved <= lastmoved
                    iter = iter + 1;
                    if display > 2 % 'iter'
                        if usePool
                            fprintf(dispfmt,labindx,iter,2,length(moved),totsumD);
                        else
                            fprintf(dispfmt,iter,2,length(moved),totsumD);
                        end
                    end
                    if iter >= maxit, break; end
                    nummoved = 0;
                end
                nummoved = nummoved + 1;
                lastmoved = moved;
                
                oidx = idx(moved);
                nidx = nidx(moved);
                totsumD = totsumD + Del(moved,nidx) - Del(moved,oidx);
                
                %更新類的索引向量、新舊類別各自的樣本數目和中心
                idx(moved) = nidx;
                m(nidx) = m(nidx) + 1;
                m(oidx) = m(oidx) - 1;
                switch distance
                    case {'sqeuclidean','cosine','correlation'}
                        C(:,nidx) = C(:,nidx) + (X(:,moved) - C(:,nidx)) / m(nidx);
                        C(:,oidx) = C(:,oidx) - (X(:,moved) - C(:,oidx)) / m(oidx);
                end
                changed = sort([oidx nidx]);
            end % phase two
            
        end % nested function
        
    end

end % main function

%------------------------------------------------------------------

function D = distfun(X, C, dist, iter,rep, reps)
%DISTFUN計算樣本點到中心的距離

switch dist
    case 'sqeuclidean'
        D = pdist2mex(X,C,'sqe',[],[],[]);  
    case {'cosine','correlation'}
        % 樣本點已被標準化而中心點沒有,因此對它們進行標準化 
        normC = sqrt(sum(C.^2, 1));
        if any(normC < eps(class(normC))) % small relative to unit-length data points(?)
            if reps==1
                error(message('stats:kmeans:ZeroCentroid', iter));
            else
                error(message('stats:kmeans:ZeroCentroidRep', iter, rep));
            end
            
        end
        C = bsxfun(@rdivide,C,normC);
        D = pdist2mex(X,C,'cos',[],[],[]); 
end
end % function

%------------------------------------------------------------------
function [centroids, counts] = gcentroids(X, index, clusts, dist)
%GCENTROIDS Centroids and counts stratified by group.
%計算各類的樣本數目和中心點
p = size(X,1);
num = length(clusts);

centroids = NaN(p,num,'like',X);
counts = zeros(1,num,'like',X);

for i = 1:num
    members = (index == clusts(i));
    if any(members)
       counts(i) = sum(members);
       switch dist
           case {'sqeuclidean','cosine','correlation'}
              centroids(:,i) = sum(X(:,members),2) / counts(i);
      end
    end
end
end % function
 

Python 中的Kmeans

from sklearn.cluster import KMeans
import numpy as np
X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 4], [4,0]])
kmeans=KMeans(n_clusters=2,random_state=0).fit(X)