層次聚類演算法分為合併演算法和分裂演算法。合併演算法會在每一步減少聚類中心的數量，聚類產生的結果來自前一步的兩個聚類的合併；分裂演算法與合併演算法原理相反，在每一步增加聚類的數量，每一步聚類產生的結果都將是前一步聚類中心分裂得到的。合併演算法現將每個樣品自成一類，然後根據類間距離的不同，合併距離小於閾值的類。我用了基於最短距離演算法的層次聚類演算法，最短距離演算法認為，只要兩個類的最小距離小於閾值，就將兩個類合併成一個類。

1層次聚類演算法實現步驟

①獲得所有樣品特徵

②設定閾值

③將所有樣品各分一類，聚類中心等於樣品總個數。

④對所有樣品迴圈：

找到距離最近的兩類pi，pj，設定距離

若minDis<=T，則合併pi和pj否則退出迴圈。

2層次聚類演算法的程式設計實現

clear all;close all;clc;

% 第一類資料

mu1=[0 0 ];  %均值

S1=[0.1 0 ;0 0.1];  %協方差

data1=mvnrnd(mu1,S1,100);   %產生高斯分佈資料

%第二類資料

mu2=[1.25 1.25 ];

S2=[0.1 0 ;0 0.1];

data2=mvnrnd(mu2,S2,100);

% 第三個類資料

mu3=[-1.25 1.25 ];

S3=[0.1 0 ;0 0.1];

data3=mvnrnd(mu3,S3,100);

% 顯示資料

plot(data1(:,1),data1(:,2),'b+');

hold on;

plot(data2(:,1),data2(:,2),'r+');

plot(data3(:,1),data3(:,2),'g+');

grid on;

%  三類資料合成一個不帶標號的資料類

data=[data1;data2;data3]; 

[m,n]=size(data);

patternNum=m;

T=0.1;

pattern=zeros(m,n+1);

for i=1:patternNum

    pattern(i,n+1)=i;

    pattern(i,1:n)=data(i,:);

end

while 1

    minDis=inf;

    pi=0;

    pj=0;

%     尋找距離最近的兩個類計算最小距離

    for i=1:patternNum-1

        for j=i+1:patternNum

            if(pattern(i,n+1)~=pattern(j,n+1))

                tempDis=norm(pattern(i,1:n)-pattern(j,1:n));

                if(tempDis<minDis)

                    minDis=tempDis;

                    pi=pattern(i,n+1);

                    pj=pattern(j,n+1);

                end

            end

        end

    end

%     距離小於閾值則合併兩個類

    if(minDis<=T)

        if(pi>pj)

            temp=pi;

            pi=pj;

            pj=temp;

        end

        for i=1:patternNum

            if(pattern(i,n+1)==pi)

                pattern(i,n+1)=pi;

            elseif(pattern(i,n+1)>pi)

                pattern(i,n+1)=pattern(i,n+1)-1;

            end

        end

    else

        break;

    end

end

disp('ok')

[m, n]=size(pattern);

%最後顯示聚類後的資料

figure;

hold on;

for i=1:m

    if pattern(i,n)==1  

         plot(pattern(i,1),pattern(i,2),'r*');

    elseif pattern(i,n)==2

         plot(pattern(i,1),pattern(i,2),'g*');

    elseif pattern(i,n)==3

         plot(pattern(i,1),pattern(i,2),'b*');

    elseif pattern(i,n)==4

         plot(pattern(i,1),pattern(i,2),'y*');

    else

         plot(pattern(i,1),pattern(i,2),'m*');

    end

end

grid on;

3層次聚類演算法測試結果：

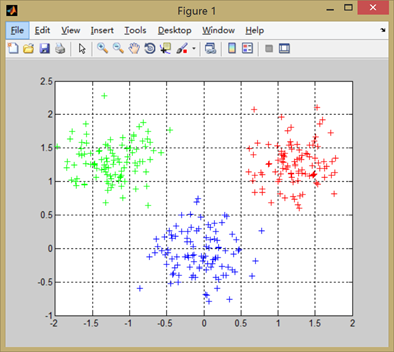
下圖是產生的高斯數對及當閾值設定為T=0.1的時候的結果：

當T=0.5時的結果：

可見當閾值設的比較大時所有的都將成為一類。所以閾值的設定很重要。

基於最小距離的層次聚演算法對類間距要求很高，例如將高斯數對的協方差加大，產生距離比較近的數對時，層次聚類演算法就會出現很大問題如下圖：

但是在相同的生成引數下，kmeans卻有很好的效果：