在影象的基本仿射變換中，經常會碰到經過旋轉、縮放後灰度值如何賦值的問題。因為變換之後，影象的座標位置有可能是小數，所以就需要插值演算法來確定到底將該畫素賦予哪個位置。

1、最鄰近插值法(Nearest Interpolation)

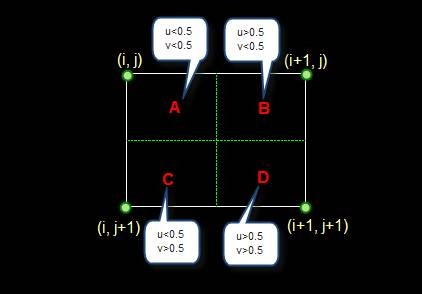
這是最簡單的一種插值方法，不需要計算。在待求畫素的四鄰畫素中，將距離待求畫素最近的鄰接畫素灰度值賦予待求畫素。設i+u, j+v(i, j為正整數， u, v為大於零小於1的小數，下同)為待求象素座標，則待求象素灰度的值 f(i+u, j+v) 如下圖所示：

如果(i+u, j+v)落在A區，即u<0.5, v<0.5，則將左上角象素的灰度值賦給待求象素，同理，落在B區則賦予右上角的象素灰度值，落在C區則賦予左下角象素的灰度值，落在D區則賦予右下角象素的灰度值。

最鄰近元法計算量較小，但可能會造成插值生成的影象灰度上的不連續，在灰度變化的地方可能出現明顯的鋸齒狀。

2、雙線性內插法(Bilinear Interpolation)

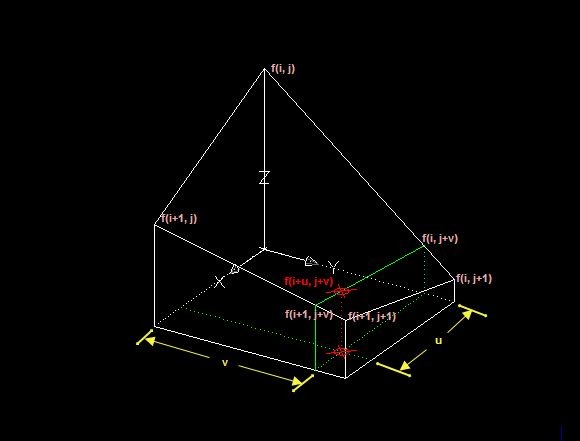
雙線性內插法是利用待求象素四個鄰象素的灰度在兩個方向上作線性內插，如下圖所示：

對於 (i, j+v)，f(i, j) 到 f(i, j+1) 的灰度變化為線性關係，則有：

f(i, j+v) = [f(i, j+1) - f(i, j)] * v + f(i, j)

同理對於 (i+1, j+v) 則有：

f(i+1, j+v) = [f(i+1, j+1) - f(i+1, j)] * v + f(i+1, j)

從f(i, j+v) 到 f(i+1, j+v) 的灰度變化也為線性關係，由此可推匯出待求象素灰度的計算式如下：

f(i+u, j+v) = (1-u) * (1-v) * f(i, j) + (1-u) * v * f(i, j+1) + u * (1-v) * f(i+1, j) + u * v * f(i+1, j+1)

雙線性內插法的計算比最鄰近點法複雜，計算量較大，但沒有灰度不連續的缺點。它具有低通濾波性質，使高頻分量受損，影象輪廓可能會有一點模糊。影象看起來更光滑。

下面貼上主要實驗程式碼：

//nearest interpolation method for resize(zoom)
void onNearest(CDib &m_Dib, BYTE **srcImg,BYTE **dstImg,int h,int w,double zoomNumber)
{
	int ey,ex;
	int j,i;
	int zoomH = (int)(zoomNumber*h + 0.5);
	int zoomW = (int)(zoomNumber*w + 0.5);
	int originalLineByte = ((w % 4 == 0 ? w : w + (4 - (w % 4)))*m_Dib.GetBitCount())/8; //align the width
	int zoomLineByte = ((zoomW % 4 == 0 ? zoomW : zoomW + (4 - (zoomW % 4)))*m_Dib.GetBitCount())/8;
	BYTE *temp = new BYTE[w * h];
	for(j=0;j<h;j++) //copy original image to the buffer
	{
		for(i=0;i<w;i++)
		{
			temp[j*w+i] = srcImg[j][i];  
		}
	}
	BYTE *newImg = new BYTE [zoomLineByte * zoomH];
	for(ey = 0;ey < zoomH;ey++)
	{
		for(ex = 0; ex < zoomLineByte;ex++)
		{
			j = (int)(ey/zoomNumber + 0.5); //nearest value
			i = (int)(ex/zoomNumber + 0.5);
			if((i >= 0) && (i < w) && (j >= 0)&& (j < h))
			{	
				 //memcpy(&newImg[ey * zoomLineByte] + ex * m_Dib.GetBitCount() / 8,&temp[j * originalLineByte] + i * m_Dib.GetBitCount() <span style="white-space:pre">				</span> //<span style="white-space:pre">			</span>/ 8,m_Dib.GetBitCount() / 8); 			
				newImg[ey*zoomLineByte+ex] = temp[j*originalLineByte+i];
			}
			else
			{
				newImg[ey*zoomLineByte+ex] = 255;
			}
			dstImg[ey][ex]=newImg[ey*zoomLineByte+ex];
		}
	}
}
 

//bilinear interpolation method for resize(zoom)
void onBilinear(CDib &m_Dib,BYTE **srcImg,BYTE **dstImg,int h, int w,double zoomNumber)
{
	int ey,ex;
	int j,i;
	int zoomH = (int)(zoomNumber*h + 0.5);
	int zoomW = (int)(zoomNumber*w + 0.5);
	int originalLineByte = ((w % 4 == 0 ? w : w + (4 - (w % 4)))*m_Dib.GetBitCount())/8; //align the width
	int zoomLineByte = ((zoomW % 4 == 0 ? zoomW : zoomW + (4 - (zoomW % 4)))*m_Dib.GetBitCount())/8;
	BYTE *temp = new BYTE[w * h];

	for(j=0;j<h;j++) //copy original image to the buffer
	{
		for(i=0;i<w;i++)
		{
			temp[j*w+i] = srcImg[j][i];  
		}
	}

	BYTE *newImg = new BYTE [zoomLineByte * zoomH];

	for(ey = 0;ey < zoomH;ey++)
	{
		for(ex = 0;ex < zoomLineByte;ex++)
		{
			double jz = ((double)ey)/zoomNumber;  //get the original image coordinates
			double iz = ((double)ex)/zoomNumber;
			int j1 = (int)jz;
			int i1 = (int)iz;
			int j2 = j1 + 1;
			int i2 = i1 + 1;
			double u = iz - i1;					//插值點與鄰近整數點(j1,i1)的距離 x coordinate
			double v = jz - j1;					// y coordinate

			double s1 = (1.0 - u)*(1.0 - v);		<span style="white-space:pre">	</span>//鄰近整數點(j1,i1)函式值的係數（左上角）left-up corner
			double s2 = (1.0-u)*v;				<span style="white-space:pre">	</span>//鄰近整數點(j1,i1)函式值的係數（左下角）left-down corner
			double s3 = u*(1.0 - v);				//鄰近整數點(j1,i1)函式值的係數（右上角）right-up corner
			double s4 = u*v;					//鄰近整數點(j1,i1)函式值的係數（右下角）right-down corner

			if((jz >=0) && (jz < h) && (iz >= 0) && (iz < w))
			{
				*(newImg+ey*zoomLineByte+ex) = *(temp+j1*originalLineByte+i1)*s1
					+*(temp+j1*originalLineByte+i2)*s3
					+*(temp+j2*originalLineByte+i1)*s2
					+*(temp+j2*originalLineByte+i2)*s4;
				}
				else
				{
					*(newImg+ey*zoomLineByte+ex) = 255;
				}
			dstImg[ey][ex]=newImg[ey*zoomLineByte+ex];
		}
	}
}

實驗效果如下圖所示：分別放大了1.5倍

最鄰近插值：

雙線性內插：

可以看到最鄰近插值影象中有明顯的鋸齒狀，而雙線性內插結果圖中比較光滑，也帶一點模糊的感覺。

其他參考連結：