【原】總(tu)結(cao)粒子群演算法(PSO)解決旅行商問題(TSP)
阿新 • • 發佈:2019-01-05
粒子群演算法(PSO)是一套比較經典的演算法, 旅行商問題(TSP)同樣是一個經典的問題。如果想用PSO去解決TSP問題的話,那麼應該如何去解決呢?
初看之下一陣欣喜,因為我發現,如果按照論文中的方法能夠成功的話,那麼包括布穀鳥,螢火蟲都可以通過類似的辦法進行有意義的嘗試。
按照論文的思路,我撰寫了如下程式碼
% main.m
% 呼叫
clc
clear
close all
number = 14; % 14個城市
global cities
cities = rand(number,2) * 200 - 100; % 假設城市分佈在 [-100,-100] ,[100,100]的平面內
[best,par,ItorMean,ItorBest] % PSO 演算法,globalBest為全域性最優,par是最終的粒子資訊,ItorMean是每次迭代平均適應度,ItorBest是每次迭代最佳適應度
function [globalBest,par,ItorMean,ItorBest] = PSO4TSP_v1(cities)
%% 引數設定
number_cities = size % netplot.m
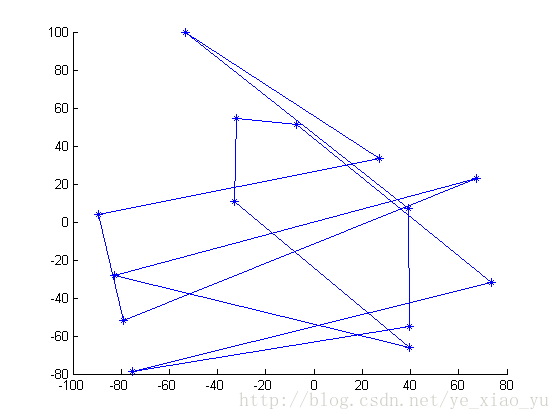
function netplot(city,n) %連線各城市,將路線畫出來
figure
hold on
plot(city(:,1),city(:,2),'*');
line([city(:,1);city(1,1)],[city(:,2);city(1,2)]);
end% fitness.m
% 計算城市間的距離
function z = fitness(n)
global cities
tstart = n;
tend = [n(2:end),n(1)];
z = sum(distance(cities(tstart,1),cities(tstart,2),cities(tend,1),cities(tend,2)));
z=1/z;
end% getSS.m
function ss = getSS(v1,v2)
% 求SS運算元
% v1,v2是一組向量,v1,v2所包含的元素應該相同。
% 若v1,v2順序相同,則返回ss = [];
% 若順序不同,則返回一個ss運算元,即v2通過ss變換可以得到v1
ss = [];
while 1
idx = find(v1 ~= v2);
if isempty(idx)
break;
end
idx2 = find(v2 == v1(idx(1)));
so = [idx(1),idx2];
ss = [ss;so];
v2 = doSO(v2,so);
end% doSS.m
function v = doSS(v,ss)
% SS操作函式
% v:之前的方案
% ss:SS運算元,用作交換(n*2)的矩陣
% v:SS操作之後的結果
if ~isempty(ss)
[m,n] = size(ss);
if m == 2 && n ~= 2
ss = ss';
m = n;
n = 2;
end
if n ~= 2
help doSS
error('ss must be n*2 matrix');
end
for i = 1 : m
v = doSO(v,ss(i,:));
end
end
end
% doSO.m
function v = doSO(v,so)
% SO操作函式
% v:之前的方案
% so:SO運算元,用作交換
% v:SO操作之後的結果
if ~isempty(so)
if length(so) ~= 2
help doSO
error('length of "so" iso must equals 2');
else
len = length(v);
if so(1) > len || so(2) > len || so(1) < 1 || so(2) < 1
help doSO
error('"so" iso is not the index of v');
else
v(so(1)) = v(so(1)) + v(so(2));
v(so(2)) = v(so(1)) - v(so(2));
v(so(1)) = v(so(1)) - v(so(2));
end
end
end
end
% getSS.m
% 論文中的減法操作
function ss = getSS(v1,v2)
% 求SS運算元
% v1,v2是一組向量,v1,v2所包含的元素應該相同。
% 若v1,v2順序相同,則返回ss = [];
% 若順序不同,則返回一個ss運算元,即v2通過ss變換可以得到v1
ss = [];
while 1
idx = find(v1 ~= v2);
if isempty(idx)
break;
end
idx2 = find(v2 == v1(idx(1)));
so = [idx(1),idx2];
ss = [ss;so];
v2 = doSO(v2,so);
end% unionSS.m
% 論文中的⊕操作
function ss = unionSS(ss1,ss2)
% ss1,ss2運算元合併操作
vm1 = max(max(ss1));
vm2 = max(max(ss2));
if isempty(ss1)
if isempty(ss2)
ss = [];
else
ss = ss2;
end
elseif isempty(ss2)
ss = ss1;
else
vm = max(vm1,vm2);
v = 1 : vm;
v2 = doSS(doSS(v,ss1),ss2);
ss = getSS(v,v2);
end
end當我信心滿滿的執行的時候,效果卻令人大跌眼鏡。
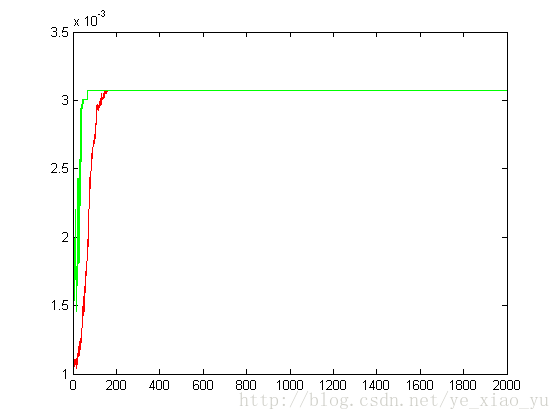
雖然從迭代的圖中能看出來,演算法確實是取尋優了而且也收斂,但是得到的最終效果卻不能令人滿意。
後來,我又查閱了相關資料,發現這兩篇帖子java版本的PSO求解TSP問題,C++版本的PSO求解TSP問題參考的同一篇文獻,而且結果同樣有不能令人接受,所以只能暫時認為這篇古老的文獻的公式出錯。
展望下未來的情況,也許可以找到更好的文獻取代這篇文獻,亦或者把之前的迭代公式改正確。
如果是後者,我們可以通過經典PSO問題類比推理出求解TSP的V’id可能需要在原先的公式加上一個隨機速度Vir。推測Vir為一個SO或者是隨著迭代次數增加而運算元長度向0收斂的SS。筆者正向這個方向進行嘗試。