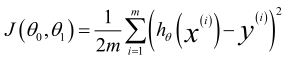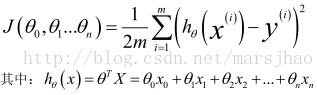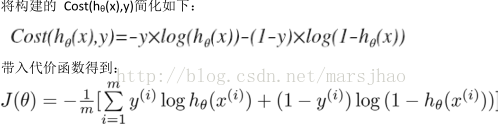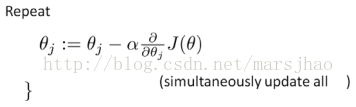本系列部落格主要摘自中國海洋大學黃海廣博士翻譯整理的機器學習課程的字幕及筆記，在我的學習過程中幫助很大，在此表示誠摯的感謝！

本系列其他部分：

一、引言

監督學習(Supervised Learning)：分類問題、迴歸問題等。

無監督學習(Unsupervised Learning）：聚類演算法等。

二、單變數線性迴歸(LinearRegression with One Variable)

一種可能的表達方式為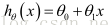：，因為只含有一個特徵/輸入變數，因此這樣的問題叫作單變數線性迴歸問題

代價函式：

梯度下降

其中α是學習率(learning rate)，它決定了我們沿著能讓代價函式下降速度最快的方向邁出步子的步長。關於學習率α的選取，若α選擇過小，則演算法需要迭代許多次才能到達全域性最小值點；若α選擇過大，可能導致在梯度下降的時候越過全域性最小值點，會導致無法收斂，甚至是發散。

此處要注意每次迭代都是同時對所有的引數同時更新。

線性迴歸模型的批量梯度下降演算法

四、多變數線性迴歸(Linear Regression with Multiple Variables)

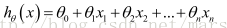
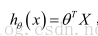
支援多變數的假設 h 表示為：，為了簡化公式表示形式，引入x₀=1，則公示簡化為：。

多變數梯度下降的代價函式：

批量梯度下降演算法：

特徵縮放

目的是將特徵值的取值約束到-1<=x_i<=1的範圍內，保證各特徵值都足夠相近，對特徵點的有等同的影響。

，x0=1。

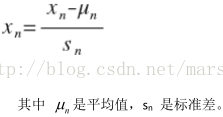
學習率

自動測試是否收斂的方法，例如將代價函式的變化值與某個閾值（例如 0.001）進行比較。當J(θ)隨迭代次數上升時，試著用更小的α（同樣適用於波浪形曲線）。通常可以考慮嘗試些學習率：α=0.01，0.03，0.1，0.3，1，3，10。

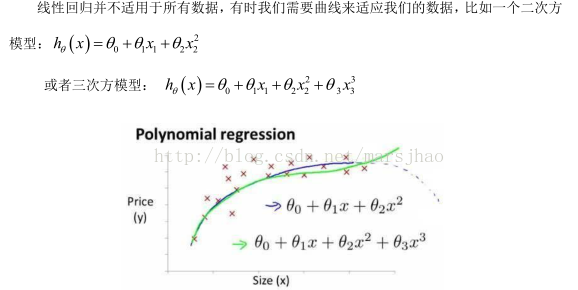
多項式迴歸

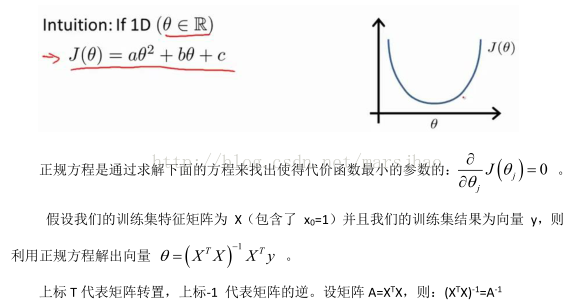
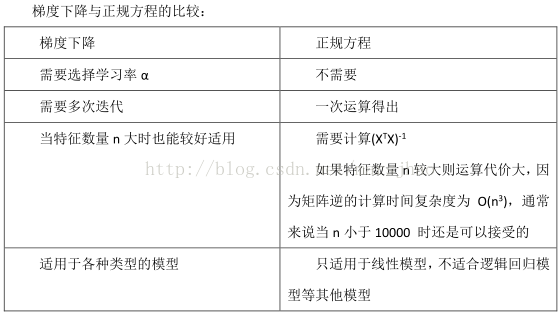
正規方程

六、邏輯迴歸(LogisticRegression)

模型表示

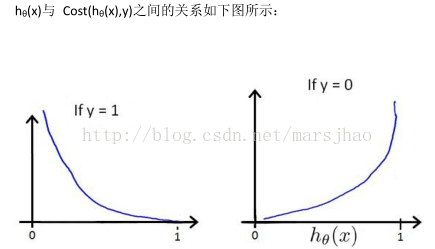
代價函式

這樣構建的Cost(hθ(x),y)函式的特點是：當實際的 y=1 且hθ也為 1 時誤差為 0，當 y=1但hθ不為1時誤差隨著 hθ的變小而變大；當實際的 y=0 且hθ也為 0 時代價為 0，當 y=0 但 hθ不為0時誤差隨著 hθ的變大而變大。

梯度下降演算法求解最優引數

在此處進行梯度下降演算法之前進行特徵縮放是必要的。

多類別分類：一對多

主要思想是將第i類定為正類，其餘類別定為負類，擬合出i個分類器，在需要做出預測時，將待預測樣本依次送入這i個分類器，得到i個h_θ(x)，並選擇取值最大的那一個分類器的分類結果。