本文在寫作過程中參考了大量資料，不能一一列舉，還請見諒。
回溯演算法的定義：回溯演算法也叫試探法，它是一種系統地搜尋問題的解的方法。回溯演算法的基本思想是：從一條路往前走，能進則進，不能進則退回來，換一條路再試。
解題的一般步驟是：
1.定義一個解空間，它包含問題的解；
2.利用適於搜尋的方法組織解空間；
3.利用深度優先法搜尋解空間；
4.利用限界函式避免移動到不可能產生解的子空間。
問題的解空間通常是在搜尋問題的解的過程中動態產生的，這是回溯演算法的一個重要特性。
話不多說，我們來看幾個具體的例子慢慢理解它：
1.八皇后問題
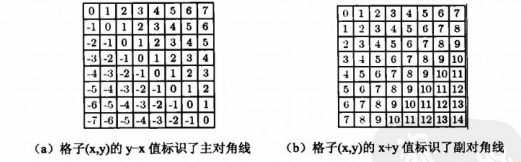
該問題是國際西洋棋棋手馬克斯·貝瑟爾於1848年提出：在8×8格的國際象棋上擺放八個皇后，使其不能互相攻擊，即任意兩個皇后都不能處於同一行、同一列或同一斜線上，問有多少種擺法。 下面的解法參考了《演算法競賽入門經典》。如果我們逐行放置皇后則肯定沒有任意兩個皇后位於同一行，只需要判斷列和對角線即可。使用一個二維陣列vis[3][]，其中vis[0][i]表示列，vis[1][i]和vis[2][i]表示對角線。因為(x,y)的y-x值標識了主對角線，x+y值標識了副對角線。由於y-x可能為負，所以存取時要加上n。

#include<cstring> 
#include<iostream>
using namespace std;  
int vis[3][15],tot;  

void search(int cur)  
{  
    int i,j;  
    if(cur==8) tot++;
    else  
    {  
    	for(i=0;i<8;i++)  
        {  
            if(!vis[0][i]&&!vis[1][cur-i+8]&&!vis[2][cur+i])  
            {  
                vis[0][i]=1;  
                vis[1][cur-i+8]=1;  
                vis[2][cur+i]=1;    
                search(cur+1);  
                //改回輔助的全域性變數 
                vis[0][i]=0;       
                vis[1][cur-i+8]=0;  
                vis[2][cur+i]=0;  
            }  
        }  
    }  
}  

int main()  
{  
    search(0);   
    cout<<tot<<endl;
}
 

2.圖的著色問題
給定無向連通圖G=(V,E)和m種不同的顏色，用這些顏色為圖G的各頂點著色，每個頂點著一種顏色。如果一個圖最少需要m種顏色才能使圖中每條邊連線的2個頂點著不同顏色，則稱m為該圖的色數。地圖著色問題可轉換為圖的著色問題：以地圖中的區域作為圖中頂點，2個區域如果鄰接，則這2個區域對應的頂點間有一條邊，即邊表示了區域間的鄰接關係。著名的四色定理就是指每個平面地圖都可以只用四種顏色來染色，而且沒有兩個鄰接的區域顏色相同。

給定圖和顏色的數目求出著色方法的數目，可以使用回溯法。

#define N 100
#include<iostream>
using namespace std;
int v,e,c,graph[N][N],color[N];
//頂點數,邊數,顏色數 
int sum;

bool ok(int k)
{
	for(int j=1;j<=v;j++)
	{
		if(graph[k][j]&&(color[j]==color[k])) return false;
	}
	return true;
}

void backtrack(int t)
{
	if(t>v) sum++;
 	else
 	{
    	for(int i=1;i<=c;i++)
		{
			color[t]=i;
   			if(ok(t)) backtrack(t+1);
   			//改回輔助的全域性變數 
   			color[t]=0;
		}
 	}
}

int main()
{
    int i,j;
    cin>>v>>e>>c;                
	for(i=1;i<=v;i++)
	{
		for(j=1;j<=v;j++)
		{
			graph[i][j]=0; 
		}
	}           
	for(int k=1;k<=e;k++)      
	{
		cin>>i>>j;
		graph[i][j]=1;
		graph[j][i]=1;
	}
	for(i=0;i<=v;i++) color[i]=0;
 	backtrack(1);
  	cout<<sum<<endl;
}
 

3.裝載問題

有一批共n個集裝箱要裝上2艘載重量分別為c1和c2的船，其中集裝箱i的重量為wi，且。裝載問題要求確定是否有一個合理的裝載方案可將這些集裝箱裝上這2艘船。如果有，找出一種裝載方案。例如當n=3，c1=c2=50且w=[10,40,40]時，則可以將集裝箱1和2裝到第一艘輪船上，而將集裝箱3裝到第二艘輪船上；如果w=[20,40,40]，則無法將這3個集裝箱都裝上輪船。容易證明，如果一個給定裝載問題有解，則首先將第一艘船儘可能裝滿再將剩餘的集裝箱裝上第二艘船可得到最優裝載方案。將第一艘船儘可能裝滿等價於選取全體集裝箱的一個子集，使該子集中集裝箱重量之和最接近c1。用回溯法解裝載問題,  時間複雜度O(2^n)，在某些情況下優於動態規劃演算法。剪枝方案是如果當前已經選擇的全部物品載重量cw+剩餘集裝箱的重量r<=當前已知的最優載重量bestw，則刪去該分支。

#include<iostream>
using namespace std;  
int n;//集裝箱數  
int w[40];//集裝箱重量
int c1,c2;//兩艘船的載重量  
int ans;//當前載重量  
int bestans;//當前最優載重量  
int r;//剩餘集裝箱重量  
  
void backtrack(int i)  
{        
    if(i>n)    
    {  
		if(ans>bestans) bestans=ans;  
		return;  
    }  
    r-=w[i];  
    if(ans+w[i]<=c1)  
    {   
      ans+=w[i];  
      backtrack(i+1);  
      //改回輔助的全域性變數 
      ans-=w[i];  
    }  
    if(ans+r>bestans) backtrack(i+1);    
    //改回輔助的全域性變數 
    r+=w[i];  
}    
  
int maxloading()  
{  
	ans=0;  
	bestans=0;  
    backtrack(1);   
    return bestans;  
}

int main()  
{    
	cin>>n>>c1>>c2;  
 	int i=1;  
 	int sum=0;  
 	//集裝箱總重量 
 	while(i<=n)  
	{  
		cin>>w[i];  
		r+=w[i];  
		sum+=w[i];  
 		i++;  
 	}    
	maxloading();  
	if(bestans>0&&((sum-bestans)<=c2)) cout<<bestans<<endl;  
 	else if(sum<=c2) cout<<bestans<<endl;  
  	else cout<<"No"<<endl;  
}

4.批處理作業排程問題
給定n個作業的集合{J1,J2,…,Jn}。每個作業必須先由機器1處理，然後由機器2處理。作業Ji需(1≤i≤n)要機器j(1≤j≤2)的處理時間為tji。對於一個確定的作業排程，設Fji是作業i在機器j上完成處理的時間。所有作業在機器2上完成處理的時間和稱為該作業排程的完成時間和：。要求對於給定的n個作業，制定最佳作業排程方案，使其完成時間和達到最小。

tji	機器1	機器2
作業1	2	1
作業2	3	1
作業3	2	3

例如，對於這張表格所示的情況，3個作業有3!=6種可能排程方案，很顯然最壞複雜度即為O(n!)。如果按照2,3,1的順序,則作業2的完成時間為4，作業3的完成時間為8，作業1的完成時間為9，完成時間和為21。最優的作業排程順序為最佳排程方案是1,3,2，其完成時間和為18。

#define MAX 200
#include<iostream>
using namespace std;
int* x1;//作業Ji在機器1上的工作時間
int* x2;//作業Ji在機器2上的工作時間
int number=0;//作業的數目
int* xorder;//作業順序
int* bestorder;//最優的作業順序
int bestvalue=MAX;//最優的時間
int xvalue=0;//當前完成用的時間
int f1=0;//機器1完成的時間
int* f2;//機器2完成的時間

void backtrack(int k)
{
	if(k>number)
	{
		for(int i=1;i<=number;i++) bestorder[i]=xorder[i];
  		bestvalue=xvalue;
	}
	else
	{
		for(int i=k;i<=number;i++)
  		{
           f1+=x1[xorder[i]];
           f2[k]=(f2[k-1]>f1?f2[k-1]:f1)+x2[xorder[i]];
           xvalue+=f2[k];
           swap(xorder[i],xorder[k]);
           if(xvalue<bestvalue) backtrack(k+1);
           swap(xorder[i],xorder[k]);
           xvalue-=f2[k];
           f1-=x1[xorder[i]];
		}
	}
}

int main()
{
	cout<<"請輸入作業數目：";
 	cin>>number;
	x1=new int[number+1];
 	x2=new int[number+1];
  	xorder=new int[number+1];
   	bestorder=new int[number+1];
   	f2=new int[number+1];
   	x1[0]=0;
   	x2[0]=0;
   	xorder[0]=0;
   	bestorder[0]=0;
    f2[0]=0;
    cout<<"請輸入每個作業在機器1上所用的時間："<<endl;
    int i;
    for(i=1;i<=number;i++)
    {
		cout<<"第"<<i<<"個作業=";
		cin>>x1[i];
  	}
	cout<<"請輸入每個作業在機器2上所用的時間："<<endl;
 	for(i=1;i<=number;i++)
  	{
   		cout<<"第"<<i<<"個作業=";
     	cin>>x2[i];
  	}
   	for(i=1;i<=number;i++) xorder[i]=i;
    backtrack(1);
    cout<<"最節省的時間為："<<bestvalue<<endl;
    cout<<"對應的方案為：";
    for(i=1;i<=number;i++) cout<<bestorder[i]<<"  ";
    cout<<endl;
}

5.再再論揹包問題
在從零開始學動態規劃和從零開始學貪心演算法中我們已經討論過了揹包問題，這裡我們再次用回溯法求解經典的零一揹包問題。

#include<iostream>
using namespace std;
int n,c,bestp;//物品個數,揹包容量,最大價值
int p[10000],w[10000],x[10000],bestx[10000];//物品的價值,物品的重量,物品的選中情況

void backtrack(int i,int cp,int cw)
{
    if(i>n)
    {
        if(cp>bestp)
        {
            bestp=cp;
            for(i=1;i<=n;i++) bestx[i]=x[i];
        }
    }
    else
	{
        for(int j=0;j<=1;j++)  
        {
            x[i]=j;
            if(cw+x[i]*w[i]<=c)  
            {
                cw+=w[i]*x[i];
                cp+=p[i]*x[i];
                backtrack(i+1,cp,cw);
                cw-=w[i]*x[i];
                cp-=p[i]*x[i];
            }
        }
	}
}

int main()
{
    bestp=0; 
    cin>>c>>n;
    for(int i=1;i<=n;i++) cin>>w[i];
    for(int i=1;i<=n;i++) cin>>p[i];
    backtrack(1,0,0);
    cout<<bestp<<endl;
}

6.最大團問題
給定無向圖G=(V, E)，U是V的子集。如果對任意u,v屬於U有(u,v)屬於E，則稱U是G的完全子圖。G的完全子圖U是G的團當且僅當U不包含在G的更大的完全子圖中。G的最大團是指G中所含頂點數最多的團。如果對任意u,v屬於U有(u, v)不屬於E，則稱U是G的空子圖。G的空子圖U是G的獨立集當且僅當U不包含在G的更大的空子圖中。G的最大獨立集是G中所含頂點數最多的獨立集。G的補圖G'=(V', E')定義為V'=V且(u, v)屬於E'當且僅當(u, v)不屬於E。
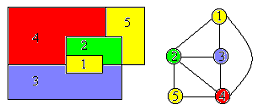
如圖所示，給定無向圖G={V, E}，其中V={1,2,3,4,5}，E={(1,2),(1,4),(1,5),(2,3),(2,5),(3,5),(4,5)}。根據最大團定義，子集{1,2}是圖G的一個大小為2的完全子圖，但不是一個團，因為它包含於G的更大的完全子圖{1,2,5}之中。{1,2,5}是G的一個最大團。{1,4,5}和{2,3,5}也是G的最大團。右側圖是無向圖G的補圖G'。根據最大獨立集定義，{2,4}是G的一個空子圖，同時也是G的一個最大獨立集。雖然{1,2}也是G'的空子圖，但它不是G'的獨立集，因為它包含在G'的空子圖{1,2,5}中。{1,2,5}是G'的最大獨立集。{1,4,5}和{2,3,5}也是G'的最大獨立集。

最大團問題可以用回溯法在O(n2^n)的時間內解決。首先設最大團為一個空團，往其中加入一個頂點，然後依次考慮每個頂點，檢視該頂點加入團之後仍然構成一個團。程式中採用了一個比較簡單的剪枝策略，即如果剩餘未考慮的頂點數加上團中頂點數不大於當前解的頂點數，可停止回溯。用鄰接矩陣表示圖G，n為G的頂點數，cn儲存當前團的頂點數，bestn儲存最大團的頂點數。當cn+n-i<bestn時，不能找到更大的團，利用剪枝函式剪去。

#include<iostream>
using namespace std;
const int maxnum=101;
bool graph[maxnum][maxnum];
bool use[maxnum],bestuse[maxnum]; 
int cn,bestn,v,e;

void backtrack(int i)
{
    if(i>v)
    {
    	if(cn>bestn)
    	{
        	bestn=cn;
        	for(int j=1;j<=v;j++) bestuse[j]=use[j];
        	return;
    	}
    }
    bool flag=true;
    for(int j=1;j<i;j++)
    {
    	if(use[j]&&!graph[j][i])
        {
            flag=false;
            break;
        }
    }
    if(flag)
    {
        cn++;
        use[i]=true;
        backtrack(i+1);
        use[i]=false;
        cn--;
    }
    if(cn+v-i>bestn)  
    {
        use[i]=false;
        backtrack(i+1);
    }
}

int main()
{
    cin>>v>>e;
    for(int i=1;i<=e;i++)
    {
    	int p1,p2;
    	cin>>p1>>p2;
  		graph[p1][p2]=true;
  		graph[p2][p1]=true;
    }
    backtrack(1);
    cout<<bestn<<endl;
    for(int i=1;i<=v;i++) 
	{
		if(bestuse[i]) cout<<i<<" ";
	}
    cout<<endl;  
}

7.圓排列問題

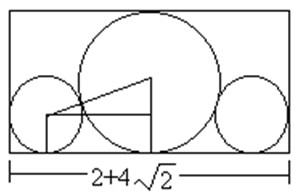
給定n個大小不等的圓c1,c2,…,cn，現要將這n個圓排進一個矩形框中，且要求各圓與矩形框的底邊相切。圓排列問題要求從n個圓的所有排列中找出有最小長度的圓排列。例如，當n=3，且所給的3個圓的半徑分別為1，1，2時，這3個圓的最小長度的圓排列如圖所示。其最小長度為。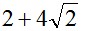

注意，下面程式碼中圓排列的圓心橫座標以第一個圓的圓心為原點。所以，總長度為第一個圓的半徑+最後一個圓的半徑+最後一個圓的橫座標。

#include<cmath>
#include<iostream>
#include<algorithm>
using namespace std;
float minlen=10000,x[4],r[4];//當前最優值,當前圓排列圓心橫座標,當前圓排列
int n;//圓排列中圓的個數

//計算當前所選擇圓的圓心橫座標
float center(int t)
{
    float temp=0;
	for(int j=1;j<t;j++)
	{
		//由x^2=sqrt((r1+r2)^2-(r1-r2)^2)推導而來
        float valuex=x[j]+2.0*sqrt(r[t]*r[j]);
		if(valuex>temp) temp=valuex;
    }
    return temp;
}

//計算當前圓排列的長度
void compute()
{
    float low=0,high=0;
	for(int i=1;i<=n;i++)
	{
		if(x[i]-r[i]<low) low=x[i]-r[i];
        if(x[i]+r[i]>high) high=x[i]+r[i];
    }
    if(high-low<minlen) minlen=high-low;
}

void backtrack(int t)
{
    if(t>n) compute();
    else
	{
		for(int j=t;j<=n;j++)
		{
			swap(r[t],r[j]);
			float centerx=center(t);
			if(centerx+r[t]+r[1]<minlen)
			{
				x[t]=centerx;
				backtrack(t+1);
			}
			swap(r[t],r[j]);
		}
	}
}

int main()
{
	n=3; 
	r[1]=1,r[2]=1,r[3]=2;
	cout<<"各圓的半徑分別為："<<endl;
	for(int i=1;i<=3;i++) cout<<r[i]<<" ";
	cout<<endl;
	cout<<"最小圓排列長度為：";
	backtrack(1);
	cout<<minlen<<endl;
}

上述演算法尚有許多改進的餘地。例如，像1,2,…,n-1,n和n,n-1, …,2,1這種互為映象的排列具有相同的圓排列長度，只計算一個就夠了。而且，如果所給的n個圓中有k個圓有相同的半徑，則這k個圓產生的k!個完全相同的圓排列，也只需要計算一個。 
8.連續郵資問題
假設國家發行了k種不同面值的郵票，並且規定每張信封上最多隻允許貼h張郵票。連續郵資問題要求對於給定的k和h的值，給出郵票面值的最佳設計，在1張信封上可貼出從郵資1開始，增量為1的最大連續郵資區間。例如，當k=5和h=4時，面值為(1,3,11,15,32)的5種郵票可以貼出郵資的最大連續郵資區間是1到70。UVA165就是一道這樣的典型例題。用stampval來儲存各個面值，用maxval來儲存當前所有面值能組成的最大連續面值。那麼，stampval[0] 一定等於1，因為1是最小的正整數。相應的，maxval[0]=1*h。接下去就是確定第二個，第三個......第k個郵票的面值了。對於stampval[i+1]，它的取值範圍是stampval[i]+1~maxval[i]+1。 stampval[i]+1是因為這一次取的面值肯定要比上一次的面值大，而這次取的面值的上限是上次能達到的最大連續面值+1， 是因為如果比這個更大的話， 那麼就會出現斷層， 即無法組成上次最大面值+1這個數了。 舉個例子， 假設可以貼3張郵票，有3種面值，前面2種面值已經確定為1,2， 能達到的最大連續面值為6， 那麼接下去第3種面值的取值範圍為3～7。如果取得比7更大的話會怎樣呢？ 動手算下就知道了，假設取8的話， 那麼面值為1,2,8，將無法組合出7。直接遞歸回溯所有情況， 便可知道最大連續值了。

#include<cstdio>  
#include<cstdlib>  
#include<cstring>   
#include<iostream>  
#define MAXN 200  
using namespace std;  
int h,k,ans[MAXN],stampval[MAXN],maxval[MAXN],maxstampval;  
bool vis[MAXN];  

//標記每種取到的錢數 
void mark(int n,int m,int sum)
{  
    if(m>h) return;  
	vis[sum]=true;
    for(int i=1;i<=n;++i) mark(n,m+1,sum+stampval[i]);    
}  
  
void backtrack(int cur)
{  
    if(cur>k)
	{  
        if(maxval[cur-1]>maxstampval)
		{  
            maxstampval=maxval[cur-1];  
            memcpy(ans,stampval,sizeof(stampval));  
        }  
        return;  
    }  
    for(int i=stampval[cur-1]+1;i<=maxval[cur-1]+1;++i)
	{  
        memset(vis,0,sizeof(vis));  
        stampval[cur]=i;  
        mark(cur,0,0);  
        int num=0,j=1;  
        while(vis[j++]) ++num;  
        maxval[cur]=num;  
        backtrack(cur+1);  
    }  
}  
  
int main()
{   
	while(scanf("%d %d",&h,&k),h+k)
	{  
		maxval[1]=h;  
        stampval[1]=1;  
        maxstampval=-1;  
        backtrack(2);  
        for(int i=1;i<=k;++i) printf("%3d",ans[i]);  
        printf("->%3d\n",maxstampval);  
    }    
} 

直接遞迴的求解複雜度太高，不妨嘗試計算用不超過m張面值為x[1:i]的郵票貼出郵資k所需的最少郵票數y[k]。通過y[k]可以很快推出r的值。事實上，y[k]可以通過遞推在O(n)時間內解決。這裡就不再講解了。
9.符號三角形問題
下圖是由14個“+”和14個“-”組成的符號三角形，第一行有n個符號。2個同號下面都是“+”，2個異號下面都是“-”。

符號三角形問題要求對於給定的n，計算有多少個不同的符號三角形，使其所含的“+”和“-”的個數相同。在第1行前i個符號x[1:i]確定後，就確定了1個由i(i+1)/2個符號組成的三角形。下一步確定第i+1個符號後，在右邊再加1條邊，就可以擴充套件為前i+1個符號x[1:i+1]對應的新三角形。這樣依次擴充套件，直到x[1:n]。最終由x[1:n]所確定的符號三角形中含"+"號個數與"-"個數同為n(n+1)/4。因此，當前符號三角形所包含的“+”個數與“-”個數均不超過n*(n+1)/4，可以利用這個條件剪支。對於給定的n，當n*(n+1)/2為奇數時，顯然不存在包含的"+"號個數與"-"號個數相同的符號三角形。在回溯前需要簡單的判斷一下。

#include<iostream>  
using namespace std;   
int n,half,counts,p[100][100],sum;
//第一行的符號個數,n*(n+1)/4,當前"+"號個數,符號三角矩陣,已找到的符號三角形數               
  
void backtrack(int t)  
{  
    if((counts>half)||(t*(t-1)/2-counts>half)) return;  
    if(t>n) sum++;    
    else  
    {  
		for(int i=0;i<2;i++)   
        {  
            p[1][t]=i;//第一行符號  
            counts+=i;//當前"+"號個數  
            for(int j=2;j<=t;j++)   
            {  
                p[j][t-j+1]=p[j-1][t-j+1]^p[j-1][t-j+2];  
                counts+=p[j][t-j+1];  
            }  
            backtrack(t+1);  
            for(int j=2;j<=t;j++)  
            {  
                counts-=p[j][t-j+1];  
            }  
            counts-=i;  
        }  
    }  
}   

int main()  
{
	cin>>n;  	
	half=n*(n+1)/2;  
    if(half%2==1)
    {
		cout<<"共有0個不同的符號三角形。"<<endl;
		return 0;
    }
    half=half/2;   
    backtrack(1);  
    cout<<"共有"<<sum<<"個不同的符號三角形。"<<endl;
} 

10.集合劃分問題
給定一個圖，圖中任意兩點的距離已知，請你把這個圖的所有的點分成兩個子集，要求兩個子集之間的所有點的距離和最大。對於圖中的每一個點，我們可以設一個數組，用0和1表示屬於哪個子集。

#include<iostream> 
using namespace std;   
int graph[25][25]; 
int set[25]; 
int ans,n;
    
void backtrack(int x,int sum) 
{  
    int temp;
    if(x>n) 
    {  
        if(sum>ans) ans=sum; 
        return; 
    } 
    //不選
    set[x]=0;
    temp=0;
    for(int i=1;i<=x;i++) 
    { 
        if(!set[i]) continue;
        temp+=graph[i][x];
    } 
    backtrack(x+1,sum+temp); 
    //選
    set[x]=1;
    temp=0; 
    for(int i=1;i<=x;i++) 
    { 
        if(set[i]) continue; 
        temp+=graph[i][x];
    }   
    backtrack(x+1,sum+temp);   
}  
   
int main() 
{  
    cin>>n;  
    for(int i=1;i<=n;i++) 
    { 
        for(int j=1;j<=n;j++) 
        { 
            cin>>graph[i][j];  
        } 
    }   
    backtrack(1,0); 
    cout<<ans<<endl;
}

關於回溯演算法的基礎知識就簡要介紹到這裡，希望能作為大家繼續深入學習的基礎。