問題描述：

給定任意兩個字串，比如：str1=“abcd”和str2=“gbcdz”,計算這兩個字串間的相似度。計算兩字串的相似度可等價於計算將str1變換到str2所需要的最少步驟。

問題分析：

為計算將str1變換到str2所需最小操作步驟，必須先對變換操作進行定義：

1. 修改一個字元（如把“a”替換為“g”）;
2. 增加一個字元（如把“abcd”變為“abcdz”）;
3. 刪除一個字元（如把“travelling”變為“traveling”）;

字串變換過程中執行了上述三個操作之間的任一操作，則兩字串間距離就加1。例如將上文中的str1變換到str2，即“abcd”到“gbcdz”，通過“abcd”->（操作1）->“gbcd”->（操作2）->“gbcdz”,需進行一次修改和一次新增字元操作，故兩字串距離為2，那麼字串相似度則為距離+1的倒數，即1/3=0.333。這是由俄羅斯科學家Vladimir Levenshtein在1965年提出這個概念。因此也叫Levenshtein Distance。

那麼如果給定兩個任意字串，如何計算它們距離呢？

問題解決：

解決此問題最好的方法是採用動態規劃的方法。如下：

設str1=“abcd”，str2=“gbcdz”，定義一個二維陣列d[][]，d[i][j]表示str1中取前i個字元和str2中取前j個字元的最短距離，例如d[3][2]表示“abc”到“gb”的最短距離。

d[i][j]的計算規則有三條：

• 來自d[i - i][j - 1]，即 “str1的前i-1個字元組成的子串” 到 “str2的前j-1個字元組成的子串” 的最小距離，此時如果str1[i] = str2[j]，則最短距離不變，否則最短距離加1（即把str1[i]變為str2[j] ），所以d[i][j] = d[i - 1][j - 1] + (str1[i] == str2[j] ? 0 : 1)
• 來自d[i - 1][j]，即 “A的前i-1個字元組成的子串” 到 “B的前j個字元組成的子串” 的編輯距離。此時刪除在A的第i個位置上的字元即可，所以d[i][j] = d[i - 1][j] + 1
• 來自d[i][j - 1], 即 “A的前i個字元組成的子串” 到 “B的前j-1個字元組成的子串” 的編輯距離。此時在A的子串後面新增一個字元B[j]即可，所以d[i][j] = d[i][j - 1] + 1
  於是狀態轉移方程：d[i][j] = min (d[i - 1][j - 1] + (str1[i] == str2[j] ? 0 : 1) , d[i - 1][j] + 1 , d[i][j - 1] + 1)

例如str1=“abcd”，str2=“gbcdz”的d[][]就為（注意i，j的取值範圍）：

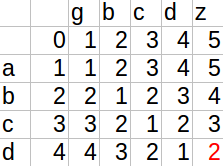
程式碼實現(anycodex.com線上編譯器測試通過，試一試？)：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int min(int a, int b, int c);
int calc(char* a, char* b);

int main(void){
printf("%d",calc("abcd", "gbcdz"));
return EXIT_SUCCESS;
}
int min(int a, int b, int c)
{
    if(a > b)
        a = b;
    if(a > c)
        a = c;
    return a;
}
int calc(char* a, char* b)
{
    int lenA = strlen(a);
    int lenB = strlen(b);
    int d[lenA+1][lenB+1];
    for(int i=0;i<=lenA;++i)
        d[i][0] = i;
    for(int i=0;i<=lenB;++i)
        d[0][i] = i;
    for(int i=1;i<=lenA;++i)
        for(int j=1;j<=lenB;++j)
            d[i][j] = min(d[i-1][j-1] + (a[i-1] == b[j-1] ? 0:1), d[i-1][j]+1, d[i][j-1]+1);
    return d[lenA][lenB];
}