SVM支援向量機高斯核調參小結
轉自http://www.cnblogs.com/pinard/p/6117515.html
在支援向量機(以下簡稱SVM)的核函式中,高斯核(以下簡稱RBF)是最常用的,從理論上講, RBF一定不比線性核函式差,但是在實際應用中,卻面臨著幾個重要的超引數的調優問題。如果調的不好,可能比線性核函式還要差。所以我們實際應用中,能用線性核函式得到較好效果的都會選擇線性核函式。如果線性核不好,我們就需要使用RBF,在享受RBF對非線性資料的良好分類效果前,我們需要對主要的超引數進行選取。本文我們就對scikit-learn中 SVM RBF的調參做一個小結。
1. SVM RBF 主要超引數概述
如果是SVM分類模型,這兩個超引數分別是懲罰係數C
懲罰係數C 即我們在之前原理篇裡講到的鬆弛變數的係數。它在優化函式裡主要是平衡支援向量的複雜度和誤分類率這兩者之間的關係,可以理解為正則化係數。當C 比較大時,我們的損失函式也會越大,這意味著我們不願意放棄比較遠的離群點。這樣我們會有更加多的支援向量,也就是說支援向量和超平面的模型也會變得越複雜,也容易過擬合。反之,當C C比較小時,意味我們不想理那些離群點,會選擇較少的樣本來做支援向量,最終的支援向量和超平面的模型也會簡單。scikit-learn中預設值是1。
另一個超引數是RBF核函式的引數γ。回憶下RBF
核函式K(x,z)=exp(γ||x−z|| 2 )γ>0
,γ主要定義了單個樣本對整個分類超平面的影響,當γ 比較小時,單個樣本對整個分類超平面的影響比較大,更容易被選擇為支援向量,反之,當γ比較大時,單個樣本對整個分類超平面的影響比較小,不容易被選擇為支援向量,或者說整個模型的支援向量也會少。scikit-learn中預設值是1樣本特徵數
如果把懲罰係數C 和RBF核函式的係數γ一起看,當C 比較大, γ比較小時,我們會有更多的支援向量,我們的模型會比較複雜,容易過擬合一些。如果C 比較小
, γ
以上是SVM分類模型,我們再來看看回歸模型。
SVM迴歸模型的RBF核比分類模型要複雜一點,因為此時我們除了懲罰係數C 和RBF核函式的係數γγ之外,還多了一個損失距離度量ϵ 。如果是nu-SVR的話,損失距離度量ϵ 代替為分類錯誤率上限nu,由於損失距離度量ϵ 和分類錯誤率上限nu起的作用等價,因此本文只討論帶距離度量ϵ 的迴歸SVM。
對於懲罰係數C C和RBF核函式的係數γ,迴歸模型和分類模型的作用基本相同。對於損失距離度量ϵ ,它決定了樣本點到超平面的距離損失,當ϵ比較大時,損失|y i −w∙ϕ(x i )−b|−ϵ |較小,更多的點在損失距離範圍之內,而沒有損失,模型較簡單,而當ϵ 比較小時,損失函式會較大,模型也會變得複雜。scikit-learn中預設值是0.1。
如果把懲罰係數C ,RBF核函式的係數γ γ和損失距離度量ϵ 一起看,當C 比較大, γ 比較小,ϵ比較小時,我們會有更多的支援向量,我們的模型會比較複雜,容易過擬合一些。如果C 比較小 , γ比較大,ϵ 比較大時,模型會變得簡單,支援向量的個數會少。
2. SVM RBF 主要調參方法
對於SVM的RBF核,我們主要的調參方法都是交叉驗證。具體在scikit-learn中,主要是使用網格搜尋,即GridSearchCV類。當然也可以使用cross_val_score類來調參,但是個人覺得沒有GridSearchCV方便。本文我們只討論用GridSearchCV來進行SVM的RBF核的調參。
我們將GridSearchCV類用於SVM RBF調參時要注意的引數有:
1) estimator :即我們的模型,此處我們就是帶高斯核的SVC或者SVR
2) param_grid:即我們要調參的引數列表。 比如我們用SVC分類模型的話,那麼param_grid可以定義為{"C":[0.1, 1, 10], "gamma": [0.1, 0.2, 0.3]},這樣我們就會有9種超引數的組合來進行網格搜尋,選擇一個擬合分數最好的超平面係數。
3) cv: S折交叉驗證的折數,即將訓練集分成多少份來進行交叉驗證。預設是3,。如果樣本較多的話,可以適度增大cv的值。
網格搜尋結束後,我們可以得到最好的模型estimator, param_grid中最好的引數組合,最好的模型分數。
下面我用一個具體的分類例子來觀察SVM RBF調參的過程
3. 一個SVM RBF分類調參的例子
這裡我們用一個例項來講解SVM RBF分類調參。推薦在ipython notebook執行下面的例子。
首先我們載入一些類的定義。

import numpy as np import matplotlib.pyplot as plt from sklearn import datasets, svm from sklearn.svm import SVC from sklearn.datasets import make_moons, make_circles, make_classification %matplotlib inline

接著我們生成一些隨機資料來讓我們後面去分類,為了資料難一點,我們加入了一些噪音。生成資料的同時把資料歸一化
X, y = make_circles(noise=0.2, factor=0.5, random_state=1); from sklearn.preprocessing import StandardScaler X = StandardScaler().fit_transform(X)
我們先看看我的資料是什麼樣子的,這裡做一次視覺化如下:

from matplotlib.colors import ListedColormap cm = plt.cm.RdBu cm_bright = ListedColormap(['#FF0000', '#0000FF']) ax = plt.subplot() ax.set_title("Input data") # Plot the training points ax.scatter(X[:, 0], X[:, 1], c=y, cmap=cm_bright) ax.set_xticks(()) ax.set_yticks(()) plt.tight_layout() plt.show()

生成的圖如下, 由於是隨機生成的所以如果你跑這段程式碼,生成的圖可能有些不同。
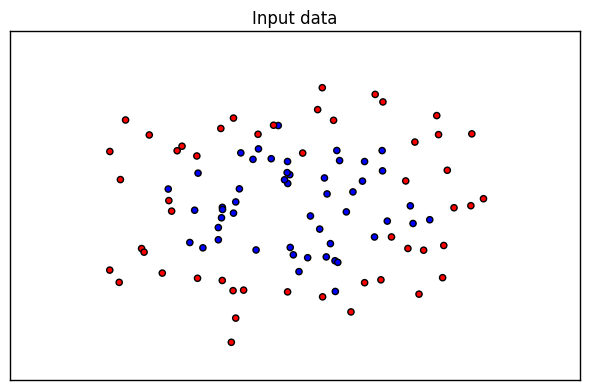
好了,現在我們要對這個資料集進行SVM RBF分類了,分類時我們使用了網格搜尋,在C=(0.1,1,10)和gamma=(1, 0.1, 0.01)形成的9種情況中選擇最好的超引數,我們用了4折交叉驗證。這裡只是一個例子,實際運用中,你可能需要更多的引數組合來進行調參。
from sklearn.model_selection import GridSearchCV grid = GridSearchCV(SVC(), param_grid={"C":[0.1, 1, 10], "gamma": [1, 0.1, 0.01]}, cv=4) grid.fit(X, y) print("The best parameters are %s with a score of %0.2f" % (grid.best_params_, grid.best_score_))
最終的輸出如下:
The best parameters are {'C': 10, 'gamma': 0.1} with a score of 0.91
也就是說,通過網格搜尋,在我們給定的9組超引數中,C=10, Gamma=0.1 分數最高,這就是我們最終的引數候選。
到這裡,我們的調參舉例就結束了。不過我們可以看看我們的普通的SVM分類後的視覺化。這裡我們把這9種組合各個訓練後,通過對網格里的點預測來標色,觀察分類的效果圖。程式碼如下:

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max,0.02),
np.arange(y_min, y_max, 0.02))
for i, C in enumerate((0.1, 1, 10)):
for j, gamma in enumerate((1, 0.1, 0.01)):
plt.subplot()
clf = SVC(C=C, gamma=gamma)
clf.fit(X,y)
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
plt.xlabel(" gamma=" + str(gamma) + " C=" + str(C))
plt.show()

生成的9個組合的效果圖如下:
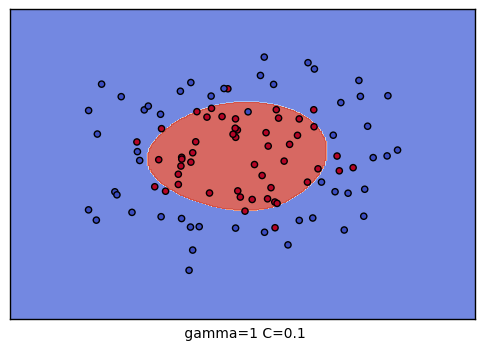


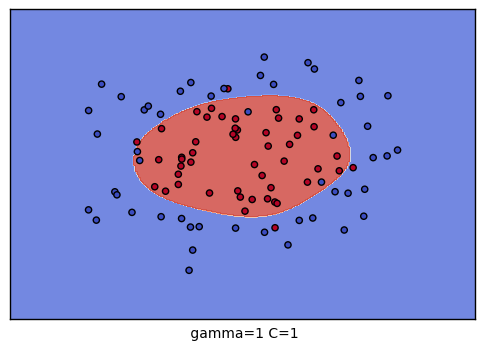
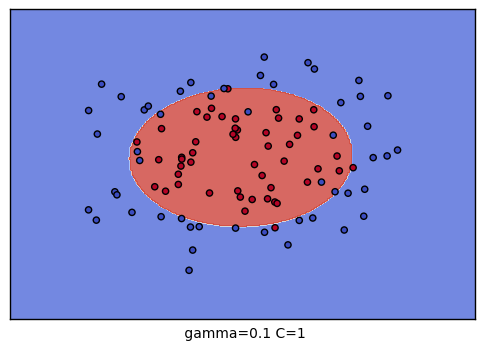
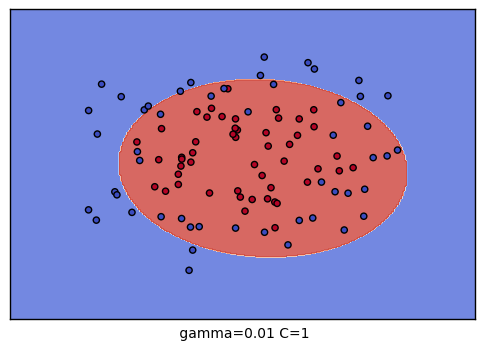
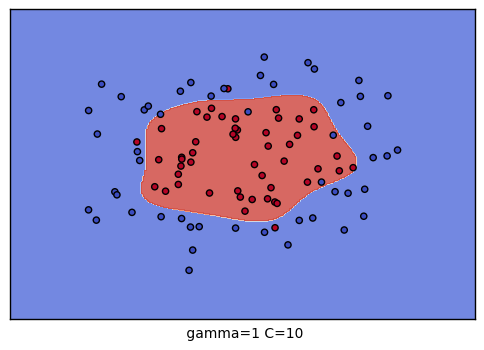


以上就是SVM RBF調參的一些總結,希望可以幫到朋友們。
