概念：

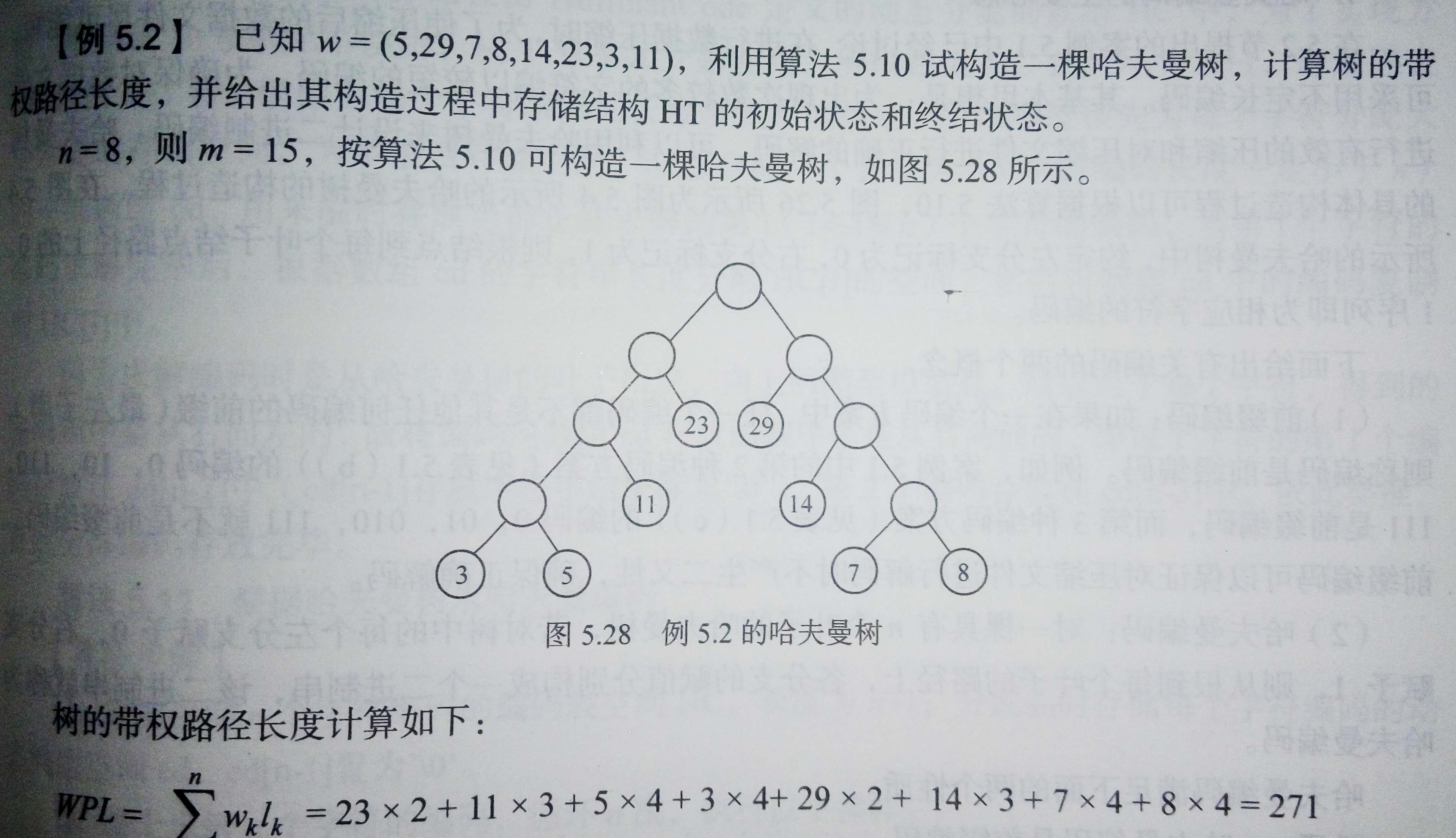
哈夫曼（Huffman）樹又稱最優二叉樹或最優搜尋樹，是一種帶權路徑長度最短的二叉樹。在許多應用中，常常賦給樹中結點一個有某種意義的實數，稱此實數為該結點的權。從樹根結點到該結點之間的路徑長度與該結點上權的乘積稱為結點的帶權路徑長度(WPL)，樹中所有葉子結點的帶權路徑長度之和稱為該樹的帶權路徑長度.
具體解釋：http://lib.csdn.net/article/datastructure/13562

演算法思想：

(1) 以權值分別為W1,W2．．．Ｗｎ的ｎ各結點，構成n棵二叉樹T1,T2,．．．Tn並組成森林F={T1,T2,．．．Tn},其中每棵二叉樹 Ti僅有一個權值為 Wi的根結點；

(2) 在F中選取兩棵根結點權值最小的樹作為左右子樹構造一棵新二叉樹，並且置新二叉樹根結點權值為左右子樹上根結點的權值之和（根結點的權值=左右孩子權值之和，葉結點的權值= Wi）

(3) 從F中刪除這兩棵二叉樹，同時將新二叉樹加入到F中;

(4) 重複(2)、(3)直到F中只含一棵二叉樹為止，這棵二叉樹就是Huffman樹。

演算法實現

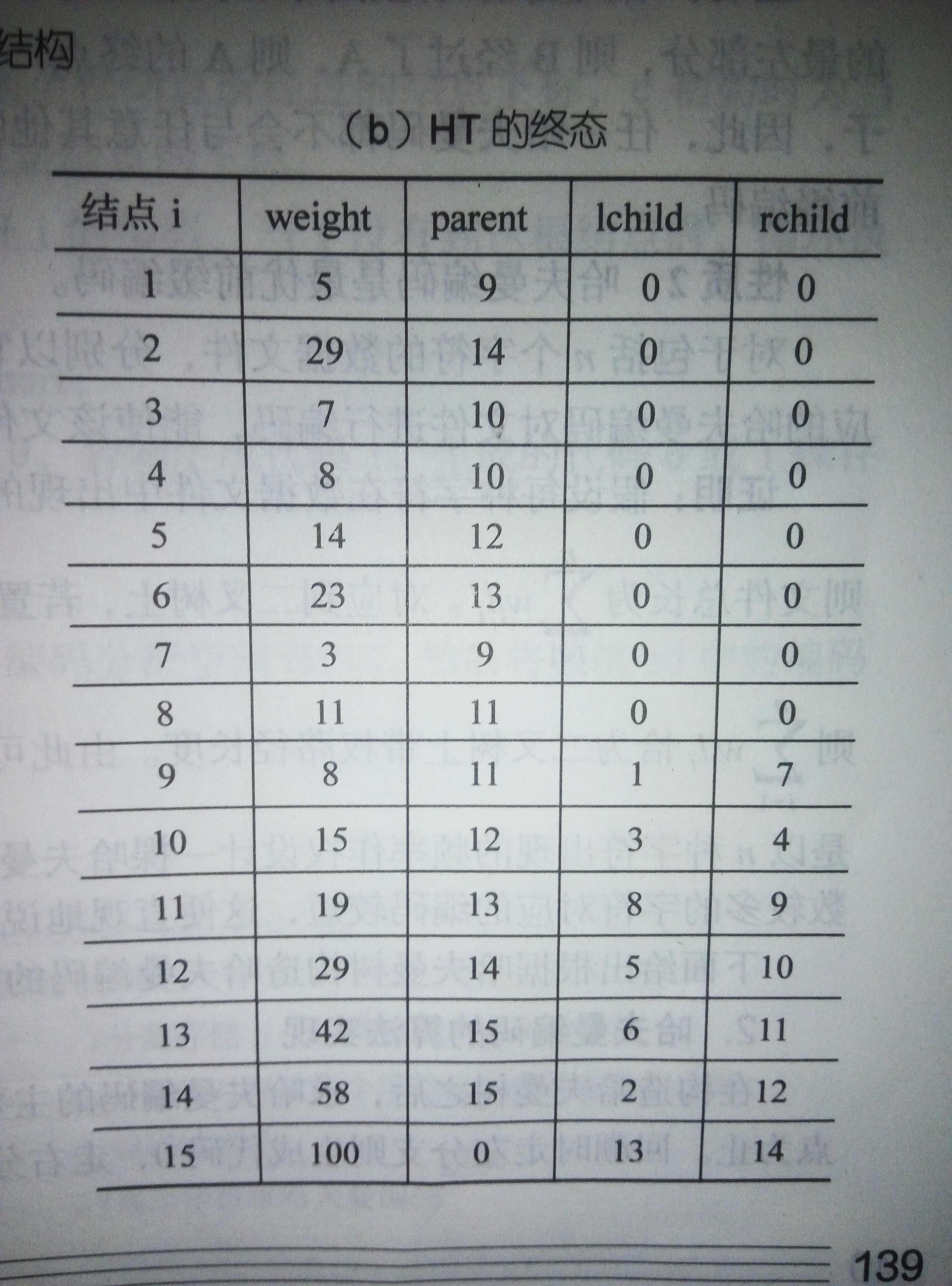
這裡我們使用陣列來儲存二叉樹，由於哈夫曼樹中沒有度為1的節點，則一顆有n個葉子節點的哈夫曼共有2n-1個節點，可以儲存在一個大小為2n-1的陣列中。每個節點的結構表示為：

//哈夫曼樹的儲存表示
typedef struct
{
    int weight;    // 權值
 

    int parent, lChild, rChild;    // 雙親及左右孩子的下標 
}HTNode, *HuffmanTree;

哈夫曼樹的節點儲存在分配動態陣列中，為了實現方便，陣列的0號元素不使用，從1開始使用。葉子節點分佈在前[1, n]，後面[n + 1, 2n - 1]（長度為n）儲存非葉子節點。
（參考《資料結構（C語言版）（第二版）》（嚴蔚敏編）第138頁）

C++程式碼

#include <iostream>
#include <iomanip>
using namespace std;

//哈夫曼樹的儲存表示
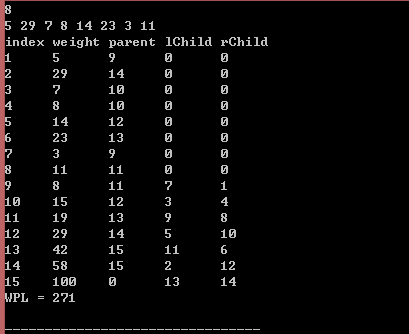
typedef struct
 

{
    int weight;    // 權值
    int parent, lChild, rChild;    // 雙親及左右孩子的下標 
}HTNode, *HuffmanTree;


// 選擇權值最小的兩顆樹 
void SelectMin(HuffmanTree hT, int n, int &s1, int &s2)
{
    s1 = s2 = 0;

    int i;
    for(i = 1; i < n; ++ i){
        if(0 == hT[i].parent){
            if(0 == s1){
                s1 = i;
            }
            else{
                s2 = i;
                break;
            }
        }
    }
    if(hT[s1].weight > hT[s2].weight){
        int t = s1;
        s1 = s2;
        s2 = t;
    }

    for(i += 1; i < n; ++ i){
        if(0 == hT[i].parent){
            if(hT[i].weight < hT[s1].weight){
                s2 = s1;
                s1 = i;
            }else if(hT[i].weight < hT[s2].weight){
                s2 = i;
            }
        }
    }
}

// 構造有n個權值（葉子節點）的哈夫曼樹 
void CreateHufmanTree(HuffmanTree &hT)
{
    int n, m;
    cin >> n;
    m = 2*n - 1;

    hT = new HTNode[m + 1];    // 0號節點不使用 
    for(int i = 1; i <= m; ++ i){
        hT[i].parent = hT[i].lChild = hT[i].rChild = 0;
    }
    for(int i = 1; i <= n; ++ i){
        cin >> hT[i].weight;    // 輸入權值 
    }
    hT[0].weight = m;    // 用0號節點儲存節點數量 

    /****** 初始化完畢, 建立哈夫曼樹 ******/
    for(int i = n + 1; i <= m; ++ i){
        int s1, s2;
        SelectMin(hT, i, s1, s2);

        hT[s1].parent = hT[s2].parent = i;
        hT[i].lChild = s1; hT[i].rChild = s2;    // 作為新節點的孩子 
        hT[i].weight = hT[s1].weight + hT[s2].weight;    // 新節點為左右孩子節點權值之和 
    }
}

int HuffmanTreeWPL_(HuffmanTree hT, int i, int deepth)
{
    if(hT[i].lChild == 0 && hT[i].rChild == 0){
        return hT[i].weight * deepth;
    }
    else{
        return HuffmanTreeWPL_(hT, hT[i].lChild, deepth + 1) + HuffmanTreeWPL_(hT, hT[i].rChild, deepth + 1);
    }
}

// 計算WPL（帶權路徑長度） 
int HuffmanTreeWPL(HuffmanTree hT)
{
    return HuffmanTreeWPL_(hT, hT[0].weight, 0);
}

// 輸出哈夫曼樹各節點的狀態 
void Print(HuffmanTree hT)
{
    cout << "index weight parent lChild rChild" << endl;
    cout << left;    // 左對齊輸出 
    for(int i = 1, m = hT[0].weight; i <= m; ++ i){
        cout << setw(5) << i << " ";
        cout << setw(6) << hT[i].weight << " ";
        cout << setw(6) << hT[i].parent << " ";
        cout << setw(6) << hT[i].lChild << " ";
        cout << setw(6) << hT[i].rChild << endl;
    }
}

// 銷燬哈夫曼樹 
void DestoryHuffmanTree(HuffmanTree &hT)
{
    delete[] hT;
    hT = NULL;
}

int main()
{
    HuffmanTree hT;
    CreateHufmanTree(hT);
    Print(hT); 
    cout << "WPL = " << HuffmanTreeWPL(hT) << endl;
    DestoryHuffmanTree(hT);
    return 0;
}

用書上的例子做驗證：

執行結果：