一、模型儲存

1.ckpt檔案

網上教程中，最常用的儲存模型的格式就是 .ckpt ，儲存這種格式的模型只需要使用 tf.train.Saver() 命令。儲存所有變數的方法如下：

saver = tf.train.Saver(tf.global_variables())
saver.save(sess, 'glasses_results/glasses_age.chkp')

如需只要儲存部分變數可以參考官網給出的方法
儲存之後的 .ckpt 模型由四個檔案組成。
其中 .data 檔案儲存了訓練過程中所有的權重 weights ， .meta 檔案儲存了所有的metadata。 .ckpt 模型可以理解成儲存訓練過程的一種狀態，因此可以在此基礎上重新訓練，比如增加訓練資料。

2.graph檔案：

graph 是儲存圖的定義檔案，不包含全權重資訊，因此相比 .ckpt 模型檔案，它的檔案體積小。

tf.train.write_graph(sess.graph_def, './glasses_results', 'model_age.pb', as_text=True)

二、固化模型

1. python固化程式碼分析

實際上使用訓練得到模型時，需要把權重固定，不然每次測試一張圖片就相當與繼續訓練模型，權重也要重新變化一次，這會導致測試一張圖片需要很久的時間。在固定權重的基礎上，還需要整合圖的定義。這個過程就是 freeze graph 。
TensorFlow提供了

$ python freeze_graph.py --input_graph=glasses_results/model_glasses.pb --input_checkpoint=glasses_results/graph_glasses.chkp --output_graph=glasses_results/frozen_graph_glasses.pb --output_node_names=output/output
Converted 378 variables to const ops.
1651 ops in the final graph.

儲存的 frozen_model 的大小理論上應該是大於權重檔案 .data 。

for op in graph.get_operations():
    print(op.name)

匯入 frozen_graph 之後，簡單的使用例項如下：

graph = load_graph(frozen_model_filename)
images = graph.get_tensor_by_name('prefix/inputs_placeholder:0')
y = graph.get_tensor_by_name('prefix/output/output:0')
with tf.Session(graph=graph) as sess:
    coder = ImageCoder()
    image_batch = make_batch(image_file, coder, False)
    softmax_output = tf.nn.softmax(y)
    batch_results = sess.run(softmax_output, feed_dict={images:image_batch.eval()})
    output = batch_results[0]
    best = np.argmax(output)
    best_choice = list[best]
    return best_choice

2. iOS平臺上的固化

我們將要建立的app會載入之前訓練好的模型，並作出預測。之前在train.py中，我們將圖儲存到了 /tmp/voice/graph.pb檔案中。但是你不能在IOS app中直接載入這個計算圖，因為圖中的部分操作是TensorFlow C++庫並不支援。所以就需要用到上面我們構建的那兩個工具。

freeze_graph將包含訓練好的w和 b的graph.pb**和檢查點檔案合成為一個檔案，並移除*IOS*不支援的操作。在終端執行*TensorFlow*目錄下的這個工具：**

    bazel-bin/tensorflow/python/tools/freeze_graph \
    --input_graph=/tmp/voice/graph.pb --input_checkpoint=/tmp/voice/model \
    --output_node_names=model/y_pred,inference/inference --input_binary \
    --output_graph=/tmp/voice/frozen.pb

最終輸出/tmp/voice/frozen.pb檔案，只包含得到y_pred和inference的節點，不包括用來訓練的節點。freeze_graph 也將權重儲存進了檔案，就不用再單獨載入。

二、簡化模型

optimize_for_inference工具進一步簡化了可計算圖，它以frozen.pb作為輸入，以/tmp/voice/inference.pb作為輸出。這就是我們將嵌入IOS app中的檔案，按如下方式執行這個工具：

bazel-bin/tensorflow/python/tools/optimize_for_inference \
--input=/tmp/voice/frozen.pb --output=/tmp/voice/inference.pb \
--input_names=inputs/x --output_names=model/y_pred,inference/inference \
--frozen_graph=True

三、量化模型

還可參考前文為什麼八個二進位制位對深度神經網路足夠了，主要講的是良好訓練的神經網路必須能應對訓練資料中的無關資訊，這成就了神經網路對輸入噪聲和計算誤差的強壯性。

很高興我們釋出了 TensorFlow 的八位量化支援的第一個版本。注意這裡的“位”是指二進位制位 (bit)。我努力促成在嵌入式視覺化峰會之前完成，因為這對低功耗以及移動裝置很重要。

神經網路發展過程中最大的挑戰是：能讓它工作起來就了不起了！這意味著訓練階段的精度和速度擁有最高優先順序。採用浮點數是保證精度的最簡單方法，而 GPU 正適合用來加速這些計算，因此自然而然沒太多人關注別的數值格式。

如今，有許多模型正在被開發出來用於商業環境。訓練的計算需求隨著研究人員的增加而增加，但用於推斷的計算量正比於使用者數。那意味著純粹的推斷效率成了許多團隊火燒眉毛的問題。

那就是用得著“量化”的地方。這是一個概括性術語，涵蓋了許多不同的技術，用來儲存數字並且針對這些數字進行計算，格式比 32 位浮點數更緊湊。這裡著重談八位定點數。

為何量化能工作

神經網路的訓練是一個不斷對權重新增細微修正的過程，這種細微修正一般需要浮點精度才能完成 (儘管也有工作試圖從這個階段開始就量化，比如二值化神經網路)。

用一個訓練好的模型來做推斷，則是另一回事。深度網路的一個魔力特性就是能夠很好地應對較大的輸入噪聲。比如為了識別照片中的物體，網路必須忽略所有的 CCD 噪聲、光照變化，以及其它與之前訓練樣本之間的非本質差異，而只關注重要的相似之處。這種能力意味著神經網路似乎把低精度計算視為另一種噪聲來源，而在數值格式精度較低的情況下仍能給出準確結果。

為何要量化

神經網路可能會佔據很大的儲存空間，比如最初的浮點數格式的 AlexNet 大小就有 200 MB。這個大小几乎全部來自神經元連線的權重，因為單個模型裡可能就有數百萬或者更多個連線。由於它們都是略微不同的浮點數，常見的像 zip 這樣的壓縮格式不會壓縮很多。值得注意的是，神經元按層組織，在每層內的權重在一定範圍內 (比如從 -3 到 6) 趨向正態分佈。

一個最簡單的壓縮方案是，儲存每層的最大和最小值，然後把這個區間線性分成 256 個離散值，於是此範圍內的每個浮點數可以用八位 (二進位制) 整數來表示，近似為離得最近的那個離散值。比如，最小值是 -3 而最大值是 6 的情形，0 位元組表示 -3，255 表示 6，而 128 是 1.5。計算細節之後再說，因為涉及到一些微妙的東西，但大致說來就是可以把檔案大小縮小 75%，使用的時候轉換回普通的浮點數就可以仍舊使用原來的程式碼。

另一個做量化的原因是，通過完全使用八位格式的輸入和輸出來降低推斷計算需要的計算資源。這個實現起來要難很多，因為需要修改所有涉及計算的地方，但可能帶來額外的回報。八位數值的存取相對浮點數而言記憶體頻寬降到 25%，這樣可以更好地利用快取並且避免 RAM 存取瓶頸。你還能使用“單指令多資料流” (SIMD) 操作實現在每個時鐘週期進行更多操作。如果你使用能加速八位運算的數字訊號處理 (DSP) 晶片，還能得到更多好處。

使用八位表示能讓模型執行更快，能耗也更低 (這對移動裝置尤其重要)，並且還對那些不能高效執行浮點運算的嵌入式系統開放了大門，這讓面向物聯網世界的大量應用成為可能。

為什麼不直接用低精度表示來訓練？

已經有一些使用低精度數值表示的實驗了，但那些結果似乎表明，你需要高於八位的精度來處理後向傳播和梯度。這讓訓練的實施更復雜，所以僅在推斷時使用低精度比較合理。目前已經有了許多大家熟悉的基於浮點數的模型，所以如果能直接針對它們進行變換的話會很方便。

如何量化模型？

TensorFlow 自帶對八位運算的生產級支援。它也能把浮點模型轉換為等價的使用量化計算進行推斷的圖 (Graph；TensorFlow 裡用來表達計算過程和內部狀態的結構)。下面是一個把最近的 GoogLeNet 轉換成八位表示的例子

1.下載模型：curl http://download.tensorflow.org/models/image/imagenet/inception-2015-12-05.tgz -o /tmp/inceptionv3.tgz
2. 解壓模型：tar xzf /tmp/inceptionv3.tgz -C /tmp/
3. 編譯量化運算元：bazel build tensorflow/contrib/quantization/tools:quantize_graph
4. 開始量化：bazel-bin/tensorflow/contrib/quantization/tools/quantize_graph \
--input=/tmp/classify_image_graph_def.pb \
--output_node_names="softmax" --output=/tmp/quantized_graph.pb \
--mode=eightbit
 ```  

這會生成一個新模型，執行的操作跟原來的模型一樣，但內部採用八位計算。你會發現新的檔案大小大致是原來的 1/4 (23 MB vs 91 MB)。你仍舊可以使用一模一樣的輸入，而結果應該是一致的。比如：

1. 編譯：bazel build tensorflow/examples/label_image:label_image
2. 執行：bazel-bin/tensorflow/examples/label_image/label_image \
   –input_graph=/tmp/quantized_graph.pb \
   –input_width=299 \
   –input_height=299 \
   –mean_value=128 \
   –std_value=128 \
   –input_layer_name=”Mul:0” \
   –output_layer_name=”softmax:0”
   “`

上面的命令運行了新的量化過的圖，而輸出的結果跟原始的很接近。

你可以對你自己的模型生成的 GraphDefs 進行同樣的操作。我建議你先用 freeze_graph 指令碼跑一遍，把一些中間檢查點的變數轉化為常數。

量化是如何進行的？

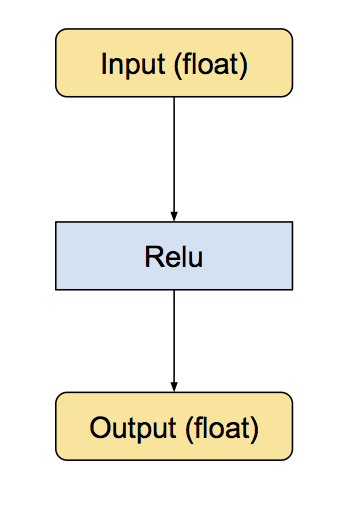
我們對量化的實現是通過把常見操作轉換為等價的八位版本達到的。涉及的操作包括卷積，矩陣乘法，活化函式，池化操作，以及拼接。轉換指令碼先把每個已知的操作替換為等價的量化版本。這包括小的子圖，它們之前之後都有轉換函式，用來把資料在浮點數和八位數之間轉換。下面是 ReLu 的例子，本來的模型輸入和輸出都是浮點數：

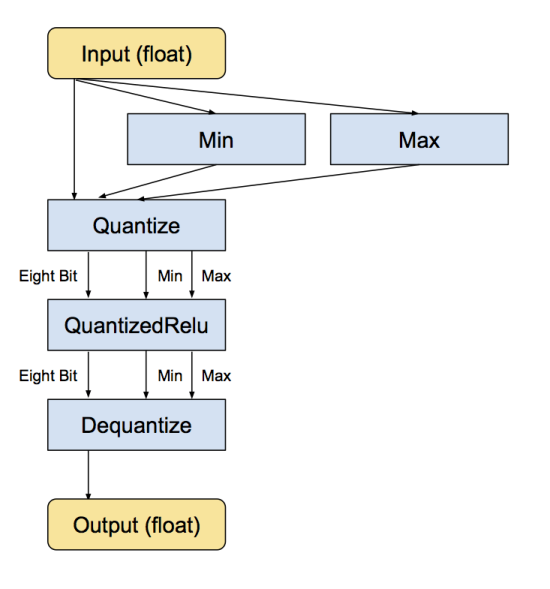
下面是等價的轉換後的子圖，輸入和輸出仍然是浮點數，但內部結構變化了，計算採用的是八位：

當每個操作被轉換成八位之後，下一步就是移除不必要的轉換。如果連續一串操作都有等價的浮點操作，則會有許多相鄰的量化/去量化操作。當發現這種模式之後，轉換程式會把相互抵消的那些操作移除，比如：

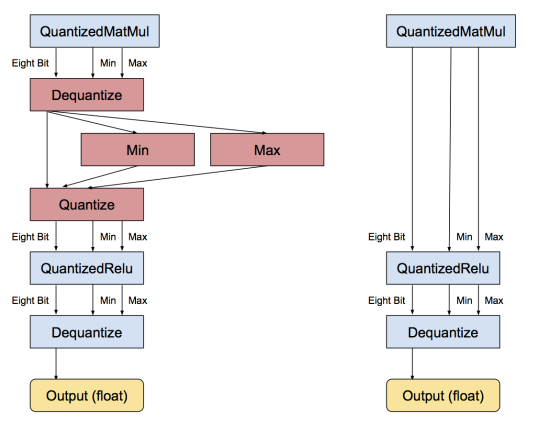
如果一個模型裡所有的操作都能被量化，那轉換後所有的操作都可用八位進行，而不需要轉換成浮點數。

量化後的張量是如何表示的？

我們前面把從浮點數到八位數的轉換描述為一個數據壓縮問題。我們知道，訓練好的神經網路模型裡，權重和活化張量的數值傾向於在相對小的範圍內取值 (比如，對於一個影象模型，權重可能在 -15 到 15 之間取值，而活化張量可能在 -500 到 1000 之間取值，當然精確值會有差異)。我們通過實驗也知道神經網路對噪聲不敏感，所以量化噪聲對結果總體來說影響不會很大。我們希望採用容易執行計算的表示，特別是大矩陣乘法這種佔據大部分時間的計算。

具體做法前面已經講了，就是儲存最小值和最大值的浮點數，然後通過把最大值和最小值之間分成 256 份來量化。也有別的壓縮方法，比如 Song Han’s code books，通過引入非線性性可以達到更小的位數，但計算上就昂貴一些。

採用清晰的量化格式的好處就是，對於那些沒有量化版本的操作而言，很容易轉換回去；對 debug 也方便。一個細節是，我們打算把最小值和最大值作為單獨的張量傳遞，這樣可以讓圖緊湊一些。

如何決定範圍？

最小值和最大值經常可以被預先算出。權重引數在載入階段就知道了，所以它們的範圍可以作為常數儲存。輸入 (比如圖片) 和活化函式也常常預先知道範圍。這避免了對一個操作的輸出進行分析來決定範圍。對於卷積或矩陣乘法來說還是得分析，因為八位的輸入會生成 32 位的結果。

如果你對八位輸入進行任何算術計算，你會自然地累積得到超過八位精度能表達的數。比如，八位數相加的結果需要九位，八位數相乘的結果需要十六位。如果你把八位乘法的結果求和 (矩陣乘法需要做這個)，結果會超過十六位，通常需要至少 20 到 25 位，取決於點乘運算有多長。

這帶來一個問題：我們需要把超過八位的輸出縮減傳遞給下一個操作。對矩陣乘法而言，一個辦法是根據可能的極端輸入計算其輸出的範圍。這是安全的，因為我們可以通過分析證明其正確性。但實際上多數權重和活化值都分佈得更均勻。這意味著實際的範圍更窄。所以，我們使用了 QuantizeDownAndShrinkRange [譯者注：這個算符實質上就是在求一個張量各元素的最大值和最小值] 操作符來分析實際的範圍。也可以通過大量的訓練資料來獲得引數範圍，然後把這些引數範圍硬編碼進去，但目前我們沒有這麼做。

舍入如何進行？

在量化的過程中，我們遇到的最難且最微妙的一個問題是偏差的累積。前面提過，神經網路對噪聲不敏感，但如果對舍入操作不小心，會導致偏差往某個方向累積，最終影響精度。你可以去原始碼中看看最終使用的公式，重要的一點是，我們需要讓舍入後的輸入值減去舍入後的最小值，而不是讓輸入值減去最小值然後才做舍入。

下一步是什麼？

我們已經證明通過八位二進位制數值表示而不是浮點數可以在移動裝置和嵌入式裝置上獲得極好的效能。你可以在 gemmlowp 看到我們用於優化矩陣乘積的框架 [譯者注：看了一下，核心部分是用匯編語言實現的，比如這個檔案；實現過程注意了快取大小，參考這個檔案；這個檔案是針對尚無優化核心程式碼的 CPU 的參考實現，沒有用匯編，演算法就是簡單的三重迴圈。]。我們還需要把從 TensorFlow 操作符學到的經驗應用到移動裝置上以獲得最佳效能。目前的量化實現可以作為一個足夠快和足夠精確的參考，可以促進對更多種裝置的八位模型支援。

如果你感興趣，推薦你仔細琢磨 TensorFlow 的量化程式碼，特別是實現操作符量化的核心部分，都包含了參考實現。