平行四邊形不等式優化DP
一.前言
DP一直是程式設計中的一個難題,解決它不僅需要大量刷題,還需要學會各種DP的方法。這裡,我就主要講一個DP的優化方法:平行四邊形不等式優化DP動態規劃。(好難呀)
二.平行四邊形不等式是個啥?
1.題目引入:猴子派對
遠離我們的世界,有一個香蕉森林。許多可愛的猴子住在那裡。有一天,作為香蕉林之王的SDH(宋大侯)決定舉辦一個盛大的聚會慶祝瘋狂香蕉日。但小猴子彼此不認識,所以作為國王,SDH必須做點什麼。
現在有n只猴子坐成一圈,每隻猴子都有交朋友的時間。而且,每隻猴子都有兩個鄰居。SDH希望將它們介紹給對方,規則是:1。每次 ,他只能介紹一隻猴子和一隻猴子的鄰居。
2.如果他介紹A和B,那麼每隻已經知道的每隻猴子A都知道每隻猴子B已經知道了,這次引入的總時間是所有猴子A和B已經知道的交友時間的總和;
3.每個小猴子都認識自己;
為了開始聚會並儘快吃香蕉,SDH想知道他需要的最短時間。
輸入
有幾個測試用例。在每種情況下,第一行是n(1≤n≤1000),這是猴子的數量。下一行包含n個正整數(小於1000),表示交朋友時間(按順序,第一個和最後一個是鄰居)。輸入是檔案結尾。
輸出
對於每種情況,您應該列印一行,給出SDH引入時的最小時間。
樣例輸入
8
5 2 4 7 6 1 3 9
樣例輸出
105
2.找出狀態轉移方程式
大家先不管圍成一個圈,先把它們看作一條直線。這道題的狀態轉移方程式很容易想到:就是在i~j號猴子的範圍內,任取一個猴子k,當成是把這個猴子左邊的那一堆猴子(i~k)介紹給它右邊的那一堆猴子(k+1~j),先預處理計算出i~j號猴子交朋友的總時間w[i][j],於是,狀態轉移方程式就出來了:
3.探索此狀態轉移方程式的性質
這可能有點難得想,大家一定要注意!
以現在的狀態轉移方程式來看是個三重迴圈,肯定要超時,不妨讓我們來優化一下這個k。k的值肯定無法在每次直接確定,那麼我們就縮小它的範圍。
首先,我們來探索一下w[i][j]的性質:有,那麼
是毋庸置疑的。還有一個性質:
,為什麼呢?這兩個加起來不應該是一樣的嗎?現在我們用平行四邊形來理解一下:
是不是就是這個道理?所以這就是著名的平行四邊形不等式。
好,現在找出了w[i][j]的規律,那麼如何是k的規律呢?這裡有一個專有名詞:最佳決策點(k),現在因為用k表示最佳決策點的話不好搞,所以我們用s[i][j]表示dp[i][j]的最佳決策點。因為w[i][j]滿足平行四邊形不等式,所以s[i][j]也會滿足平行四邊形不等式(證明過程大家自己想),則有:
如此,我們就找出了dp[i][j]的關鍵決策點的範圍了,時間就大大縮小了。
4.細節處理
只會個思路什麼都不是,現在來想一想程式碼細節問題:
1.環
這個問題很好處理,共有兩種方法:
①擷取法
因為我們的思路常常是破環成鏈,所以我們可以在整個環中每一個位置都破一遍,這有點麻煩。
②補全法
如果我們直接把整個環看成鏈是會少考慮情況的,不妨在整個鏈的後面接一個長度為(n-1)的鏈,這樣就能把所有環的情況考慮進去了。
個人推薦用補全法。
2.迴圈順序問題
因為我們關鍵決策點的範圍是,所以我們要保證s[i][j-1]和s[i+1][j]都已經求出來了,所以i從大到小迴圈,j從小到大迴圈。
求w[i][j]的方法就不用說了吧,直接用字首和相減就行了。
5.更清晰的思維
有點懵,不要慌,大家來看一下這道題的思維圖,也許就思路清晰了許多,對平行四邊形不等式優化DP有更深刻的意識。
6.程式碼
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define M 2005
#define INF 0x3f3f3f3f
#define min(a, b) a < b ? a : b
int n, Time[M], dp[M][M], s[M][M], sum[M], ans;
inline void Read (int &x){
int f = 1; x = 0; char c = getchar();
while (c > '9' || c < '0') {if (c == '-') f = -1; c = getchar();}
while (c >= '0' && c <= '9') {x = x * 10 + c - 48; c = getchar();}
x *= f;
}
int main (){
while (~scanf ("%d", &n)){
ans = INF;
for (register int i = 1; i <= n; i ++){
Read (Time[i]);
sum[i] = sum[i - 1] + Time[i];
}
for (register int i = n + 1; i < 2 * n; i ++){//sum[i]是字首和,我沒有求w[i][j]
Time[i] = Time[i - n];
sum[i] = sum[i - 1] + Time[i];
}
n = n * 2 - 1;
for (register int i = 0; i <= n; i ++)//預處理
for (register int j = 0; j <= n; j ++)
dp[i][j] = INF, s[i][j] = 0;
dp[0][0] = 0;
for (register int i = n; i >= 1; i --){
dp[i][i] = 0;
for (register int j = i + 1; j <= n; j ++){
if (!s[i][j - 1])//特殊情況,特殊處理,處理成極限值
s[i][j - 1] = min (i + 1, j - 1);
if (!s[i + 1][j])
s[i + 1][j] = j - 1;
for (register int k = s[i][j - 1]; k <= s[i + 1][j]; k ++){
if (dp[i][j] > dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1]){//sum[j] - sum[i - 1]即w[i][j]
dp[i][j] = dp[i][k] + dp[k + 1][j] + sum[j] - sum[i - 1];
s[i][j] = k;
}
}
}
}
n = (n + 1) / 2;
for (register int i = 1; i <= n; i ++)//找答案
ans = min (ans, dp[i][i + n - 1]);
printf ("%d\n", ans);
}
return 0;
}通過這道題,相信大家對平行四邊形不等式優化DP有了新的認識,下面來看一道變式。
7.變式
1.題目:樹的建造
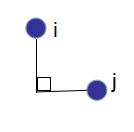
對於所有i<j,考慮一個滿足Xi<Xj和Yi>Yj的點集合(Xi,Yi)的二維空間。我們希望它們都通過一個有向樹連線,樹的邊緣向右(X正)或向上(Y正)。下圖顯示了一個示例樹。
編寫一個程式,該程式將所有給定的點與最短的邊的總長度連線起來。
輸入
輸入以包含整數N(1<=N<=1000)的行開始,即點數。然後N行跟隨。第i行包含兩個整數XI和y(0<=Xi,y<=10000),它們給出了第i點的座標。
輸出
在一行中列印邊的總長度。
樣例輸入
5
1 5
2 4
3 3
4 2
5 1
1
10000 0
樣例輸出
12
0
2.思路
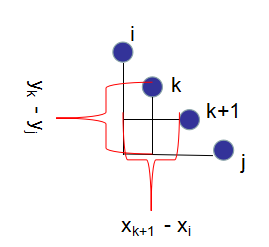
這道題就有點難了,每一個點是一組座標。但是可以像上一道題一樣解決,並且還沒有環,就把每個點看成每個猴子就行了。可以想到,連線i,j點的最小花費是,如圖:
於是,先把狀態轉移方程式寫出來:。相信大家一定是後半部分看不懂吧。大家也許想問為何不是
。因為這樣會加重複,dp[i][k]和dp[k+1][j]內已經有了
和
了,如果你想以上說的這麼加,就會把
和
又重新加一遍。
可以藉藉助一個圖來理解:
綜上,我們的狀態轉移方程式就出來了,再利用平行四邊形的性質進行優化就行了。
3.樣例程式碼
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define M 1005
#define INF 0x3f3f3f3f
struct node {
int x, y;
}a[M];
int n, dp[M][M], s[M][M];
int main (){
while (~scanf ("%d", &n)){
for (int i = 1; i <= n; i ++)
scanf ("%d %d", &a[i].x, &a[i].y);
memset (dp, INF, sizeof(dp));
memset (s, 0, sizeof(s));
dp[0][0] = 0;
for (int i = n; i >= 1; i --){
dp[i][i] = 0;
for (int j = 1 + i; j <= n; j ++){
if (!s[i][j - 1])
s[i][j - 1] = min (i + 1, j - 1);
if (!s[i + 1][j])
s[i + 1][j] = j - 1;
for (int k = s[i][j - 1]; k <= s[i + 1][j]; k ++){
if (dp[i][j] > dp[i][k] + dp[k + 1][j] + a[k].y - a[j].y + a[k + 1].x - a[i].x){
dp[i][j] = dp[i][k] + dp[k + 1][j] + a[k].y - a[j].y + a[k + 1].x - a[i].x;
s[i][j] = k;
}
}
}
}
printf ("%d\n", dp[1][n]);
}
return 0;
}三.總結
相信通過這兩道題,大家對平行四邊形不等式有了初步的概念,後面還會附上更難的題目,加油!