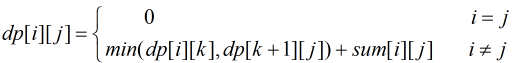藍橋杯 合併石子 DP+四邊形不等式優化
接下來一行,包含n個整數,按順序給出每堆石子的大小 。 輸出格式 輸出一個整數,表示合併的最小花費。 樣例輸入 5
1 2 3 4 5 樣例輸出 33 資料規模和約定 1<=n<=1000, 每堆石子至少1顆,最多10000顆。
思路:和藍橋杯另一個題目 矩陣乘法 同一個型別,考慮用DP求解,dp[i][j]表示把第i堆到第j堆合到一起的最小花費,則有狀態轉移方程:
其中sum[i][j]代表第i堆到第j堆的總石子數,可以用一個字首和陣列代替。
本以為這題就這麼過了,但沒想到第一發只過了7個點,剩下三個超時,然後無論我怎麼想辦法優化,都是卡在最後一個點上,最後我把狀態轉移過程中的min庫函式換掉,再把對陣列的訪問和修改換成對整數修改,最後再賦值給dp陣列,終於1900+ms擦線過了。。但我感覺這題應該有更好的方法,百度一下果然不出所料,也因此學到新知識----四邊形不等式優化DP
關於四邊形不等式優化DP的方法及證明請戳這裡。
下面是壓線過的程式碼:
然後是四邊形不等式優化,直接將時間降到了31ms。。#include<stdio.h> #include<iostream> #include<string.h> #include<string> #include<math.h> #include<algorithm> #include<queue> #include<stack> #include<set> #include<vector> #include<map> #define ll long long #define pi acos(-1) #define inf 0x3f3f3f3f #define lson l,mid,rt<<1 #define rson mid+1,r,rt<<1|1 using namespace std; typedef pair<int,int>P; const int MAXN=100010; int dp[1001][1001]; int a[1010],s[1010][1010]; int main() { //memset(dp,inf,sizeof(dp));//用memset這題也能勉強過,但是如果用下面註釋掉的那三行進行狀態轉移就會卡在最後一個點上。 int n; scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",a+i),dp[i][i]=0,a[i]+=a[i-1]; for(int len=2;len<=n;len++) { for(int i=1,j=len;j<=n;i++,j++) { int temp=inf; dp[i][j]=inf; for(int k=i;k<=j;k++) { int t=dp[i][k]+dp[k+1][j]; if(temp>t) temp=t; // int temp=dp[i][k]+dp[k+1][j]+a[j]-a[i-1];//用這三行的話會卡在最後一個點,但其實這已經是優化過的版本了, // if(temp<dp[i][j])//如果寫最簡單的dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+a[j]-a[i-1])連倒數第二個點都過不了 // dp[i][j]=temp; } dp[i][j]=temp+a[j]-a[i-1]; } } printf("%d",dp[1][n]); return 0; }
程式碼:
#include<stdio.h> #include<iostream> #include<string.h> #include<string> #include<math.h> #include<algorithm> #include<queue> #include<stack> #include<set> #include<vector> #include<map> #define ll long long #define pi acos(-1) #define inf 0x3f3f3f3f #define lson l,mid,rt<<1 #define rson mid+1,r,rt<<1|1 using namespace std; typedef pair<int,int>P; const int MAXN=100010; int dp[1001][1001]; int a[1010],s[1010][1010]; int main() { memset(dp,inf,sizeof(dp)); int n; scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",a+i),dp[i][i]=0,a[i]+=a[i-1],s[i][i]=i; for(int len=2;len<=n;len++) { for(int i=1,j=len;j<=n;i++,j++) { for(int k=s[i][j-1];k<=s[i+1][j];k++) { int temp=dp[i][k]+dp[k+1][j]+a[j]-a[i-1]; if(temp<dp[i][j]) { dp[i][j]=temp; s[i][j]=k; } } } } printf("%d",dp[1][n]); return 0; }
最後,關於合併石子問題還有一種專門的演算法-----GarsiaWachs演算法,樸素實現的複雜度為O(n^2),若加上平衡樹優化為O(nlogn),但是蒟蒻並不會平衡樹,而且網上並沒有很多關於這個演算法的證明,大多數講這個演算法的都是講如何樸素的實現,但就算是樸素的實現我看起來也很費勁。。而且這個演算法貌似並沒有其他方面的應用,就先不深入研究了吧。
相關推薦
藍橋杯 合併石子 DP+四邊形不等式優化
演算法提高 合併石子 時間限制:2.0s 記憶體限制:256.0MB 問題描述 在一條直線上有n堆石子,每堆有一定的數量,每次可以將兩堆相鄰的石子合併,合併後放在兩堆
[DP 四邊形不等式優化] 51Nod 1022 石子歸併 V2
蒟蒻不會四邊形不等式 形如 fi,j=min{fi,k+fk+1,j+wi,j}的方程 且滿足四邊形不等式和區間包含單調性 就可以用四邊形不等式優化 #include<cstdio> #
石子歸併(區間dp & 四邊形不等式優化)
基準時間限制:1 秒 空間限制:131072 KB 分值: 20 難度:3級演算法題 收藏 取消關注 N堆石子擺成一條線。現要將石子有次序地合併成一堆。規定每次只能
51nod oj 1022 石子歸併 V2 【環形區間DP----四邊形不等式優化】
題目傳送門:1022 四邊形不等式優化: m[i,j]=min{m[i,k]+m[k,j]}(s[i,j-1]≤k≤s[i+1,j]) 當m[i,j]=min{m[i,k]+m[k,j]}(i≤
石子歸併 (四邊形不等式優化
石子歸併 (四邊形不等式優化 感覺很有 不靠譜 道理 顯然樸素演算法是\(O(n^3)\)的 \(f[i][j]\)表示i到j花費的最小价值 \(f[i][j] = min(f[i][k - 1] + f[k][j] + sum[j] - sum[i - 1])\) 通過打表打出中間點K的方式 我們會發現
藍橋杯-合併石子 (經典動態規劃)
題目大意:假設有一排n堆石子,每堆石子有若干個小石子,要求將它們合併成一堆,需要花費的最小代價。而且每次合併只能將相鄰的兩堆合併,合併的代價是兩堆石子的重量之和。題目分析:因為不能合併有間隔的石子堆,所以這不是一道哈夫曼樹的例子(哈夫曼樹:利用貪心演算法,每次合併重量最小的兩
區間dp+四邊形不等式優化
mes 取數 列數 scan 自己 min oid 表示 \n 區間dp+四邊形優化 luogu:p2858 題意 給出一列數 \(v_i\),每天只能取兩端的數,第 j 天取數價值為\(v_i \times j\),最大價值?? 轉移方程 dp[i][j] :n天賣掉i.
動態規劃練習-環狀石子歸併+四邊形不等式優化
思路:環狀的直接在n後面加上a[0]-a[n]變成鏈狀即可。 這題範圍小,如果n<1000,則必須四邊形不等式優化降低複雜度為O(n^2) Code: #include <bi
石子合併 四邊形不等式優化
很明顯的區間DP,d(i, j)表示取第i堆到第j堆石子最少花費,轉移方程d(i, j) = min(d(i, k) + d(k+1, j)) + sum[j] - sum[i].
POJ 1160 Post Office (四邊形不等式優化DP)
open memset cpp 。。 ios ems max while ctype 題意: 給出m個村莊及其距離,給出n個郵局,要求怎麽建n個郵局使代價最小。 析:一般的狀態方程很容易寫出,dp[i][j] = min{dp[i-1][k] + w[k+1][j]},表示
【轉】斜率優化DP和四邊形不等式優化DP整理
dex add ive mat 整理 off code 斜率dp 好的 當dp的狀態轉移方程dp[i]的狀態i需要從前面(0~i-1)個狀態找出最優子決策做轉移時 我們常常需要雙重循環 (一重循環跑狀態 i,一重循環跑 i 的所有子狀態)這樣的時間復雜度是O(N^2)而 斜
POJ1160 Post Office (四邊形不等式優化DP)
single inpu cst class pac ios 不等式 lang rep There is a straight highway with villages alongside the highway. The highway is represented as
四邊形不等式優化DP
pla mes npos 石子歸並 分享 max turn 四邊形 namespace 記錄一下,以免忘了 對於一個形如 \[dp[i][j]=min(dp[i][k]+dp[k][j]+w[i][j])\] 的轉移方程(註意取最大值時不一定滿足四邊形不等式) 定理1 若對
BZOJ1563/洛谷P1912 詩人小G 【四邊形不等式優化dp】
set har 方案 zoj #define 證明 isp 現在 fine 題目鏈接 洛谷P1912【原題,需輸出方案】 BZOJ1563【無SPJ,只需輸出結果】 題解 四邊形不等式 什麽是四邊形不等式? 一個定義域在整數上的函數\(val(i,j)\),滿足對\(\fo
郵局加強版:四邊形不等式優化DP
一個 ica 成了 除了 i+1 -a 都是 bit oid 題目描述 一些村莊建在一條筆直的高速公路邊上,我們用一條坐標軸來描述這條公路,每個村莊的坐標都是整數,沒有兩個村莊的坐標相同。兩個村莊的距離定義為坐標之差的絕對值。我們需要在某些村莊建立郵局。使每個村莊使用與它距
CodeForces - 321E:Ciel and Gondolas (四邊形不等式優化DP)
題意:N個人排成一行,分成K組,要求每組的不和諧值之和最小。 思路:開始以為是斜率優化DP,但是每個區間的值其實已經知道了,即是沒有和下標有關的未知數了,所以沒必要用斜率。 四邊形優化。 dp[i][j]表示前j個人分為i組的最小代價。 #include<bits/stdc++.h>
區間dp 與 四邊形不等式優化 學習筆記
部落格目錄 很久之前在網上看了傳說中的四邊形不等式,然後現在發現忘光了。趁比賽前夕趕快拿來熟悉一下。 一、引入 形如: dp[i][j]=min{dp[i][k]+dp[k+1][j]+cost[i][j]} 的狀態轉移方程,如果不加優化的話ijk三層迴圈O(n
【總結】從詩人小G談DP的四邊形不等式優化
四邊形不等式 設w(x,y)w(x,y)w(x,y)是定義在整數集合上的二元函式。若對於定義域上的任何整數,a,b,c,d(a≤b≤c≤d)a,b,c,d(a\leq b\leq c\leq d)a
平行四邊形不等式優化DP——筆記
推很久推出方程後發現時間複雜度太大 TLE是不是很沮喪 優化方式及限定條件 來道例題 Post Office There is a straight highway with villages alongside the highway. The highway is r
平行四邊形不等式優化DP
一.前言 DP一直是程式設計中的一個難題,解決它不僅需要大量刷題,還需要學會各種DP的方法。這裡,我就主要講一個DP的優化方法:平行四邊形不等式優化DP動態規劃。(好難呀) 二.平行四邊形不等式是個啥? 1.題目引入:猴子派對 遠離我們的世界,