支援向量機（Support Vector Machine，簡稱SVM）是Cortes和Vapnik於1995年首先提出的，它在解決小樣本、非線性及高維模式識別中表現出許多特有的優勢，並能夠推廣應用到函式擬合等其他機器學習問題中。SVM是我們常用的一種機器學習的分類器，其中的數據設涉及拉格朗日方程，等式優化，梳數理統計等很多問題，但是我這裡並不想多說數學的問題，只是想理解其後的原理。

SVM(support vector machine)簡單的說是一個分類器，並且是二類分類器。

• Vector：通俗說就是點，或是資料。
• Machine：也就是classifier
  ，也就是分類器。

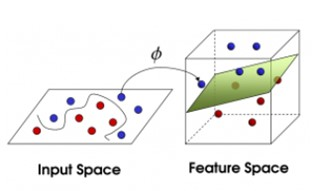
實際上((support vector)支援向量是在SVM中關鍵的概念，概念上說決定決策邊界的資料叫做支援向量，實際上我們使用SVM就是找到一個超平面，將不同類別的資料分割開來，而那個超平面就是所謂的支援向量。下面的兩個圖就是例子。

在尋找這個超平面的時候，當然遵循的規則是最大分類間隔，對於一個包含 n 個點的資料集，就像例子中所示的，我們可以很自然地找到很多可以分割如下點的線但是我們肯定很容易知道不同線的分類效果是不一樣的，比如紅線靠近下半段，而藍線幾乎是在中間的，如果一個新的資料點來了之後根據紅線的判斷它是屬於差類別的，而從藍線看來他是屬於圈類別的，這就出現瞭如何優化得到最佳分介面的問題。

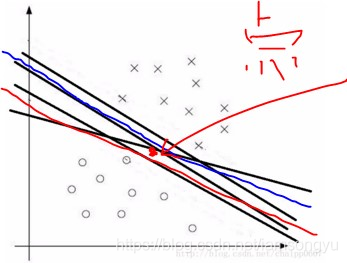
SVM中，如果存在兩類資料，我們舉例最簡單的二維資料，那麼我們就可以把資料畫在一個二維平面上，此時我想找到一個決策面（決策邊界）去將這兩類資料分開。如下圖所示： 

我們可以發現存在多個決策面可以劃分兩類資料，但是其中必然存在一個面使得對兩類資料的距離最遠也就我們所說的分類效果最佳，這對我們以後的預測工作使用積極作用的。實際的計算中，分類器通過不斷的調整直線的引數，而後通過計算直線到點距離不斷比較當前直線對分類的影響，最終找到符合要求的最佳的直線。

最大分類間隔

那麼這裡的最佳要求是什麼，什麼樣的直線才是符合要求的，那就是

SVM 通過使用最大分類間隙Maximum Margin Classifier 來設計決策最優分類超平面，而為何是最大間隔，卻不是最小間隔呢？因為最大間隔能獲得最大穩定性與區分的確信度，從而得到良好的推廣能力(超平面之間的距離越大，分離器的推廣能力越好，也就是預測精度越高，不過對於訓練資料的誤差不一定是最小。

我們可以看到分介面的直線是有一定斜率的，我們尋找距離該直線最近的兩個類別中的點，也就是粉色和藍色線所標記出來的點，在這種情況下分介面到兩側最近的距離是等長度的，也是多種情況中距離最大的，可以最清晰的將二者進行分類。

支援向量

前面也說過支援向量，實際上從名字上就能聽出來，支援向量的意思就是支撐我們分介面的向量，  可以看到兩個支撐著中間紅線的藍線和粉線，它們到中間的紅線的距離相等，即我們所能得到的最大的分類間隔 。即可以明白，在分類中一定會有這樣的資料點，根據他們來找到符合我們要求的超平面，它們用來計算距離並“支撐”我們得到的哪個超平面，而這些“支撐”的點便叫做支援向量Support Vector。

線性分類器

實際上就是上邊舉的例子。支援向量機演算法如何實現最大分類間隔的任務呢？我們可以先從線性分類器開始理解它，支援向量在沒有引入核函式的時候就是一個線性的分類器。而實際的通俗的來說，一個二維平面的分割距離的計算依靠兩個東西：

1.將資料儘量的分割在平面的兩側，如果難以分割那麼也要儘量減少分割錯誤的資料點。

2. 存在多個平面時，需要使用一個就算距離的演算法來衡量平面的好壞。

線性不可分

線性不可分，則可以理解為自變數和因變數之間的關係不是線性的。實際上，線性可不分的情況更多，我們可以通過將原始空間對映到一個高維空間，如果高維空間中資料集是線性可分的，那麼問題就可以解決了。 

可以看出來它們實際山就是計算距離的式子。

實際上舉個簡單的例子就是下面這個圖，在平面上看來確實很難分辨，但是對映到高維空間之後我們可以看到資料點變為稍微可以分割的了

matlab中的libsvm

關於來歷不想多說，在matlab下這是一個非常好用的svm工具，不過安裝的時候可能需要編譯一下才能使用，使用的方法十分簡單，在以前做東西的使用用過一段時間，並且現在涉及svm的也都是用的MATLAB的這個工具。

具體的安裝可以參考下：

https://blog.csdn.net/forever__1234/article/details/78148108

libsvm引數意義

在最初使用的時候最不能理解的就是模型訓練出來之後有一堆的引數，以前也沒有在意，後來有一段時間覺得了解一下還是有必要的，所以當時就整理了一下。

model =
Parameters: [5x1 double]
nr_class: 2
totalSV: 259
rho: 0.0514
Label: [2x1 double]
ProbA: []
ProbB: []
nSV: [2x1 double]
sv_coef: [259x1 double]
SVs: [259x13 double]

>> model.Parameters
ans =
0
2.0000
3.0000
2.8000
0

model.Parameters引數意義從上到下依次為：

• -s svm型別：SVM設定型別(預設0)
• -t 核函式型別：核函式設定型別(預設2)
• -d degree：核函式中的degree設定(針對多項式核函式)(預設3)
• -g r(gama)：核函式中的gamma函式設定(針對多項式/rbf/sigmoid核函式) (預設類別數目的倒數)
• -r coef0：核函式中的coef0設定(針對多項式/sigmoid核函式)((預設0)

即在本例中通過model.Parameters我們可以得知 –s 引數為0；-t 引數為 2；-d 引數為3；-g 引數為2.8（這也是我們自己的輸入）；-r 引數為0。

nr_class 總分類類別  Label 表示標籤
>> model.Label
ans =
1
-1
>> model.nr_class
ans =
2

model.totalSV model.nSV
>> model.totalSV
ans =
259
>> model.nSV
ans =
118
141

重要知識點：
model.totalSV代表總共的支援向量的數目，這裡共有259個支援向量；
model.nSV表示每類樣本的支援向量的數目，這裡表示標籤為1的樣本的支援向量有118個，標籤為-1的樣本的支援向量為141。

model.ProbA model.ProbB

關於這兩個引數這裡不做介紹，使用-b引數時才能用到，用於概率估計。

最後我想擷取一下一位師傅的描述 真的是很有意思

武功大俠接受別人的挑戰，要求是用一張木板將不同顏色的求分開。可是一看這根本不可能啊現在怎麼辦呢？當然像所有武俠片中一樣大俠桌子一拍，球飛到空中。然後，憑藉大俠的輕功，大俠抓起木板，插到了兩種球的中間。

現在，從空中的魔鬼的角度看這些球，這些球看起來像是被一條曲線分開了。現實一般的資料是線性不可分的，這個時候，我們就需要像大俠一樣，將小球拍起，用木板將小球進行分類。想要讓資料飛起，我們需要的東西就是核函式(kernel)，用於切分小球的木板，就是超平面。

http://blog.sina.com.cn/s/blog_6646924501018fqc.html

https://blog.csdn.net/hx14301009/article/details/79762666 

https://blog.csdn.net/u014433413/article/details/78427574

https://www.cnblogs.com/spoorer/p/6551220.html

https://blog.csdn.net/chaipp0607/article/details/73662441

https://blog.csdn.net/chaipp0607/article/details/73716226

https://www.zhihu.com/question/21094489/answer/86273196、

https://www.cnblogs.com/berkeleysong/articles/3251245.html