d[i] 是起點到 I 節點的最短距離

void Dijkstra(int s) {
    priority_queue<P, vector<P>, greater<P> > que;
    fill(d, d + MAXN, INF);
    d[s] = 0;
    que.push(make_pair(0, s));  //first:d[i] second:i 
    while (!que.empty()) {
        P p = que.top(); que.pop();
        int v = p.second;
        if
 
(d[v] < p.first) continue;    //如下圖   //d[v] < p.first 說明，v 點已經通過其他路徑變得鬆弛，距離更短。而 p.first 只是之前入隊的舊元素
        for (int i = 0; i < G[v].size(); i++) {
            edge e = edges[G[v][i]];
            if (d[e.to] > d[v] + e.cost) {
                d[e.to] = d[v] + e.cost;
                que.push(P(d[e.to], e.to));
            }
        }
    }
}
 

if(d[v] < p.first) continue;

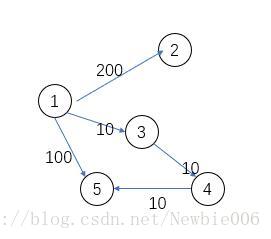
解釋：以 1 為起點，第一次遍歷會將2，3，5(I) 全部加入佇列。然後出隊3，然後4，然後更新5， 5(II)又入隊，5(II)沒有出度，然後5(II)出隊，接著第一輪的 5(I) 出隊，但是此時 5(I) 已經不是這個點已經不滿足最短路徑存在定理，所以不能再更新和5相關聯的邊，應該直接讓其出隊。也就是這個判斷條件

如果不使用這個判斷，也可以開一個 vis 陣列，用來標記，只要是更新過的節點就不能再次更新周圍的節點。