神經網路解決推薦系統問題(ONCF)
Outer Product-based Neural Collaborative Filtering(ONCF)
1)回顧CF,設計CF模型的關鍵在於:1)如何表示使用者和專案;2)如何在表示的基礎上對使用者和專案的互動進行建模。
2)回顧MF,MF是將使用者表示為潛在因素的向量(embedding),並將互動作用建模為內積—— ,正是MF使用了一個固定的、依賴於資料的函式,即函式內積作為互動作用函式,特別是在NCF中指出的MF的侷限性限制了它的表達。而且它假定嵌入維(即embedding維數)彼此相互獨立,並對所有資料點的預測做出了同樣的貢獻,如p , q。而恰恰embedding是可以解釋為專案的某些屬性不一定是獨立的,能產生更好的組合,可能是存在有不同的權重,如AFM。
然後由於NCF直接從DNN中學習,效果很不錯,只是NCF及其變體模型大多采用特徵向量內積、拼接操作的侷限性(如最上的NCF處理公式),即NCF的設計的潛在侷限性在於使用者和專案的embedding之間幾乎沒有關聯。所以原作者團隊又提出了一種基於 外積 的新的特徵互動模型ONCF,並用CNN卷積*處理學習特徵中每一維的高階相互關係,也就是顯式的捕捉嵌入維數之間的成對關聯。
首先內積與外積,向量的點乘與叉乘,一個按對應元素相乘,一個按矩陣運算相乘。
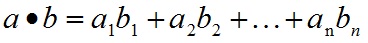
這就讓外積後的向量變成了一個能刻畫每維之間的關係的矩陣,然後就在這個特徵互動的矩陣上採用 CNN,從區域性和全域性,對每個維度進行高階的互動。模型架構如下:

模型同樣是先embedding,然後使用外積得到交叉對映 Interaction Map(是KxK的矩陣,K是embedding維數),然後使用CNN結構得到預測值,而且損失函式用了前一篇整理過的BPR損失來優化正例的排名,減少負例的影響。所以損失函式變成: 其中的D是能觀測到的正例,同樣對其使用梯度得到其他所需要的所有引數。
卷積NCF的卷積部分如下,具體也和與卷積大家族中的各位差不多。
- 對於64x64的 interaction Map,使用2x2的卷積核,啟用函式選為RELU,每層得到32個Feature Map。整體下來引數的規模也不算很大,卻又很好的學習到了互動資訊。
部分程式碼為:
def _create_placeholders(self):
with tf.name_scope("input_data"):
self.user_input = tf.placeholder(tf.int32, shape = [None, 1], name = "user_input")
self.item_input_pos = tf.placeholder(tf.int32, shape = [None, 1], name = "item_input_pos")#正例
self.item_input_neg = tf.placeholder(tf.int32, shape = [None, 1], name = "item_input_neg")#負例
self.keep_prob = tf.placeholder(tf.float32, name = "keep_prob")#dropout比率
def _conv_weight(self, isz, osz):#CNN權重
return (weight_variable([2,2,isz,osz]), bias_variable([osz]))
#卷積層
def _conv_layer(self, input, P):
conv = tf.nn.conv2d(input, P[0], strides=[1, 2, 2, 1], padding='SAME')
return tf.nn.relu(conv + P[1])
def _create_variables(self):
with tf.name_scope("embedding"):#初始化P和Q的embedding變數
self.embedding_P = tf.Variable(tf.truncated_normal(shape=[self.num_users, self.embedding_size], mean=0.0, stddev=0.01),
name='embedding_P', dtype=tf.float32) #(users, embedding_size)
self.embedding_Q = tf.Variable(tf.truncated_normal(shape=[self.num_items, self.embedding_size], mean=0.0, stddev=0.01),
name='embedding_Q', dtype=tf.float32) #(items, embedding_size)
#64x64,6層網路,所以使用6層的iszs
iszs = [1] + self.nc[:-1]
oszs = self.nc
self.P = []
for isz, osz in zip(iszs, oszs):
self.P.append(self._conv_weight(isz, osz))
self.W = weight_variable([self.nc[-1], 1])
self.b = weight_variable([1])
#卷積NCF
def _create_inference(self, item_input):
with tf.name_scope("inference"):
##分別得到embedding的P和Q
self.embedding_p = tf.nn.embedding_lookup(self.embedding_P, self.user_input)
self.embedding_q = tf.nn.embedding_lookup(self.embedding_Q, item_input)
#使用matmul函式外積 P_u 和 Q_i
self.relation = tf.matmul(tf.transpose(self.embedding_p, perm=[0, 2, 1]), self.embedding_q)
self.net_input = tf.expand_dims(self.relation, -1)
# CNN
self.layer = []
input = self.net_input
for p in self.P:
self.layer.append(self._conv_layer(input, p))
input = self.layer[-1]
# prediction
self.dropout = tf.nn.dropout(self.layer[-1], self.keep_prob)
self.output_layer = tf.matmul(tf.reshape(self.dropout,[-1,self.nc[-1]]), self.W) + self.b
return self.embedding_p, self.embedding_q, self.output_layer
ONCF通過外積操作形成一個更具表現力的二維互動對映。而互動對映可以說是非常適合CF任務,因為它不僅包含MF(其對角線)中與內積的中間結果,也產生了所有其他維度的兩兩關聯。互動對映中這種豐富的語義為以下非線性層提供了便利,從而學習可能的高階維關聯。使用了卷積神經網路學習它,從引數和規模上也合理,損失函式也採用了BRP的優化,很精彩的模型。
完整程式碼模型作者開源在 :https://github.com/duxy-me/ConvNCF
我簡陋的復現結果:
