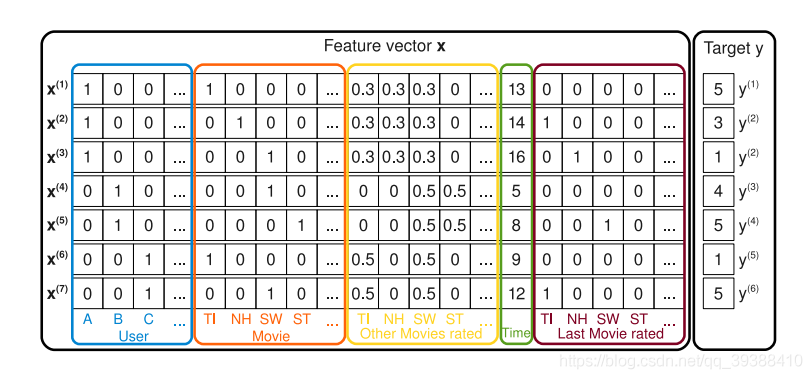
在處理MF矩陣分解時使用過FunkSVD，最後在分解誒P，Q矩陣的時候果然還是用到了一般套路，根據預測y和實際y的差別梯度下降來尋找。所以能否直接從這個思路，把它變成多個特徵的迴歸模型是否可行？ $y=w_0+$

∑ i = 1 n w i

x i ， n 表 示 特 徵 數 量 y=w_{0}+\sum\limits_{i=1}^nw_{i}x_{i}，n表示特徵數量 但是普通的線性模型，並沒有考慮到特徵與特徵之間的相互關係。所以加上一項： $y=w_{0}+\sum\limits_{i=1}^nw_{i}x_{i}+\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}w_{ij}x_{i}x_{j}$但是在資料矩陣很稀疏的情況下，即xi,xj非0的情況非常少，ωij實際上是無法僅僅通過訓練得出。於是需要引入一個輔助向量 $V_{i}=(v_{i1},v_{i2},⋯,v_{ik})^{T}$,其中k為超參，可以將y改寫成： $y=w_{0}+\sum\limits_{i=1}^nw_{i}x_{i}+\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}(v_{i}^Tv_j)x_{i}x_{j}$
即引入V：

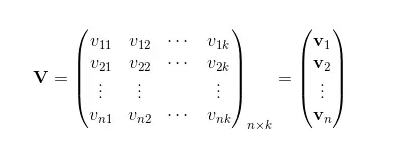
此時的互動矩陣，

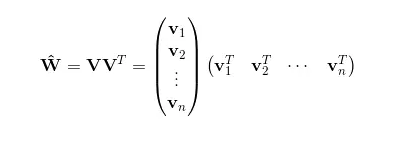
也就是說我們相對對W進行了一種矩陣分解，那麼在高稀疏上的表達上得到V相對來說是容易的。同樣我們接著要求導，先化簡一下後面的式子：

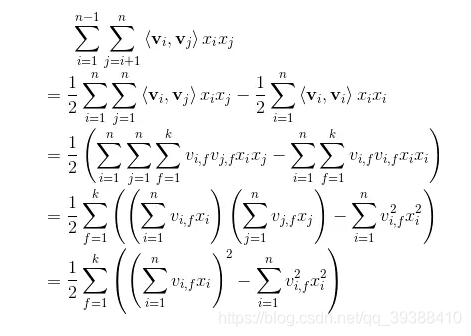
然後再求導和隨機梯度下降SGD就行了。下面使用經典的MovieLens100k資料集，也就是由明尼蘇達大學和研究人員收集整理的1000209匿名評級約3900部電影的評分。資料包括四列，使用者id，電影id，評分和時間戳。

            user  item  rating  timestamp
   0         1     1       5    874965758
   1         1     2       3    876893171
   2         1     3       4    878542960
   3         1     4       3    876893119
   4         1     5       3    889751712
   5         1     6       5    887431973
   6         1     7       4    875071561
   7         1     8       1    875072484
   8         1     9       5    878543541
   9         1    10       3    875693118

FM的程式碼為：

from itertools import count
from collections import defaultdict
from scipy.sparse import csr
import numpy as np
import pandas as pd
import numpy as np
from sklearn.feature_extraction import DictVectorizer
import tensorflow as tf
from tqdm import tqdm
#from tqdm import tqdm_notebook as tqdm

######資料處理
#將原始檔案輸入轉換成我們需要的稀疏矩陣（稀疏矩陣編碼格式）
def vectorize_dic(dic,ix=None,p=None,n=0,g=0):
    if ix==None:
        ix = dict()
        
    nz = n * g

    col_ix = np.empty(nz,dtype = int)#每行起始的偏移量

    i = 0
    for k,lis in dic.items():#遍歷文件
        for t in range(len(lis)):#遍歷每個詞
            ix[str(lis[t]) + str(k)] = ix.get(str(lis[t]) + str(k),0) + 1
            col_ix[i+t*g] = ix[str(lis[t]) + str(k)]
        i += 1

    row_ix = np.repeat(np.arange(0,n),g)#每個數對應的列號
    data = np.ones(nz)
    if p == None:
        p = len(ix)

    ixx = np.where(col_ix < p)#輸出滿足條件的值
    return csr.csr_matrix((data[ixx],(row_ix[ixx],col_ix[ixx])),shape=(n,p)),ix

#batch函式
def batcher(X_, y_=None, batch_size=-1):
    n_samples = X_.shape[0]

    if batch_size == -1:
        batch_size = n_samples
    if batch_size < 1:
       raise ValueError('Parameter batch_size={} is unsupported'.format(batch_size))

    for i in range(0, n_samples, batch_size):
        upper_bound = min(i + batch_size, n_samples)
        ret_x = X_[i:upper_bound]
        ret_y = None
        if y_ is not None:
            ret_y = y_[i:i + batch_size]
            yield (ret_x, ret_y)

#讀入資料
cols = ['user','item','rating','timestamp']
train = pd.read_csv('data/ua.base',delimiter='\t',names = cols)
test = pd.read_csv('data/ua.test',delimiter='\t',names = cols)

print(train,test)
x_train,ix = vectorize_dic({'users':train['user'].values,
                            'items':train['item'].values},n=len(train.index),g=2)


x_test,ix = vectorize_dic({'users':test['user'].values,
                           'items':test['item'].values},ix,x_train.shape[1],n=len(test.index),g=2)

#變換後的形式
print(x_train)
y_train = train['rating'].values
y_test = test['rating'].values

#得到變換後的矩陣形式
x_train = x_train.todense()
x_test = x_test.todense()

print(x_train)
print(x_train.shape)
print (x_test.shape)

#######Tensorflow搭建
#定義損失函式
n,p = x_train.shape

k = 10#設定超參k

x = tf.placeholder('float',[None,p])
y = tf.placeholder('float',[None,1])

w0 = tf.Variable(tf.zeros([1]))
w = tf.Variable(tf.zeros([p]))

v = tf.Variable(tf.random_normal([k,p],mean=0,stddev=0.01))

#y_hat = tf.Variable(tf.zeros([n,1]))

linear_terms = tf.add(w0,tf.reduce_sum(tf.multiply(w,x),1,keep_dims=True)) #按行求和
#得到化簡後的函式
pair_interactions = 0.5 * tf.reduce_sum(tf.subtract( tf.pow( tf.matmul(x,tf.transpose(v)),2), tf.matmul(tf.pow(x,2),tf.transpose(tf.pow(v,2)))),axis = 1 , keep_dims=True)

#完整的預測函式y
y_hat = tf.add(linear_terms,pair_interactions)

#正則化項
lambda_w = tf.constant(0.001,name='lambda_w')
lambda_v = tf.constant(0.001,name='lambda_v')

l2_norm = tf.reduce_sum(
    tf.add(tf.multiply(lambda_w,tf.pow(w,2)),tf.multiply(lambda_v,tf.pow(v,2))))

#error和loss
error = tf.reduce_mean(tf.square(y-y_hat))
loss = tf.add(error,l2_norm)

train_op = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(loss)#梯度下降

#模型訓練
epochs = 1
batch_size = 5000

# Launch the graph
init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)

    for epoch in tqdm(range(epochs), unit='epoch'):#輸出進行過程
        perm = np.random.permutation(x_train.shape[0])#打亂順序
        # iterate over batches
        for bX, bY in batcher(x_train[perm], y_train[perm], batch_size):
            _,t = sess.run([train_op,loss], feed_dict={x: bX.reshape(-1, p), y: bY.reshape(-1, 1)})
            print(t)


    errors = []
    for bX, bY in batcher(x_test, y_test):
        errors.append(sess.run(error, feed_dict={x: bX.reshape(-1, p), y: bY.reshape(-1, 1)}))
        print(errors)
    RMSE = np.sqrt(np.array(errors).mean())
    print (RMSE)