神經網路基本原理：

人類一向善於從大自然中尋找啟發，並做出必要的改進來滿足某種需要。而人類本身就有很多不可思議的事情，比如大腦。機器學習，學習學習，參考人類本身的學習就是對所見的事物一步一步的總結，一層一層的抽象，而大腦的神經-中樞-大腦的工作過程或許是一個不斷迭代，不斷抽象的過程，從原始的訊號，做低階的抽象，逐漸向高階抽象迭代。

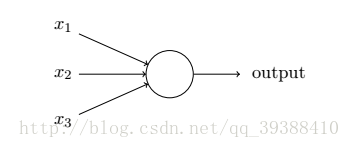
在感知機中，它採用了多個輸入單元來抽象，但是學習能力非常有限，無法解決非線性可分的問題，雖然SVM延伸了核技術解決了這一點，但是實際上利用多層的感知機（Multi-layer Perception）也能完成，不過雖然是多層，其實是隻有一層隱層節點的淺層模型。比如很多的分類，迴歸的學習方法都是淺層的演算法，在於有限的樣本和計算單元情況下對複雜的函式的表達能力有限，泛化能力不佳，計算量大。所以簡單的多層網路的學習規則肯定是不夠的，類比大腦產生更強大的演算法是必要的。

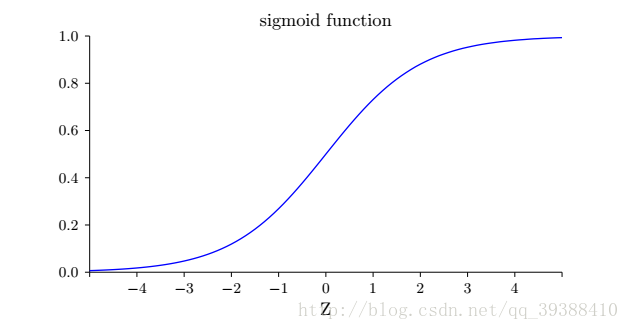
正如一個感知機一樣，它有多個輸入，不過這些輸入可以取0~1的任何值而不是僅僅0，1。改進原先的啟用函式為Sigmoid函式： $\sigma \left(z\right)=\frac{1}{1}$

+ e − z \sigma(z)=\frac{1}{1+e^{-z}}

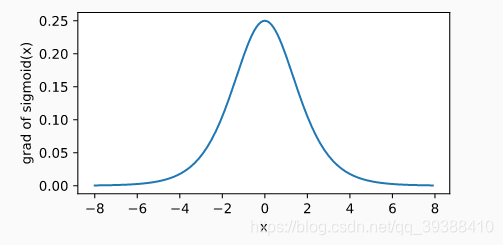
**為什麼用Sigmoid？**包括改進前的啟用函式也是一樣，都是引入非線性變換函式便於我們的“分類”。而且它的好處在於求導後的影象如下，當輸入為 0 時，sigmoid 函式的導數達到最大值 0.25；當輸入越偏離 0 時，sigmoid 函式的導數越接近 0，能過避免一些梯度的問題。其實使用不同的啟用函式最大的變化只是求偏導時某些值的改變，事實證明這樣做能夠簡化計算，至於其他的啟用函式在下面會再次總結。

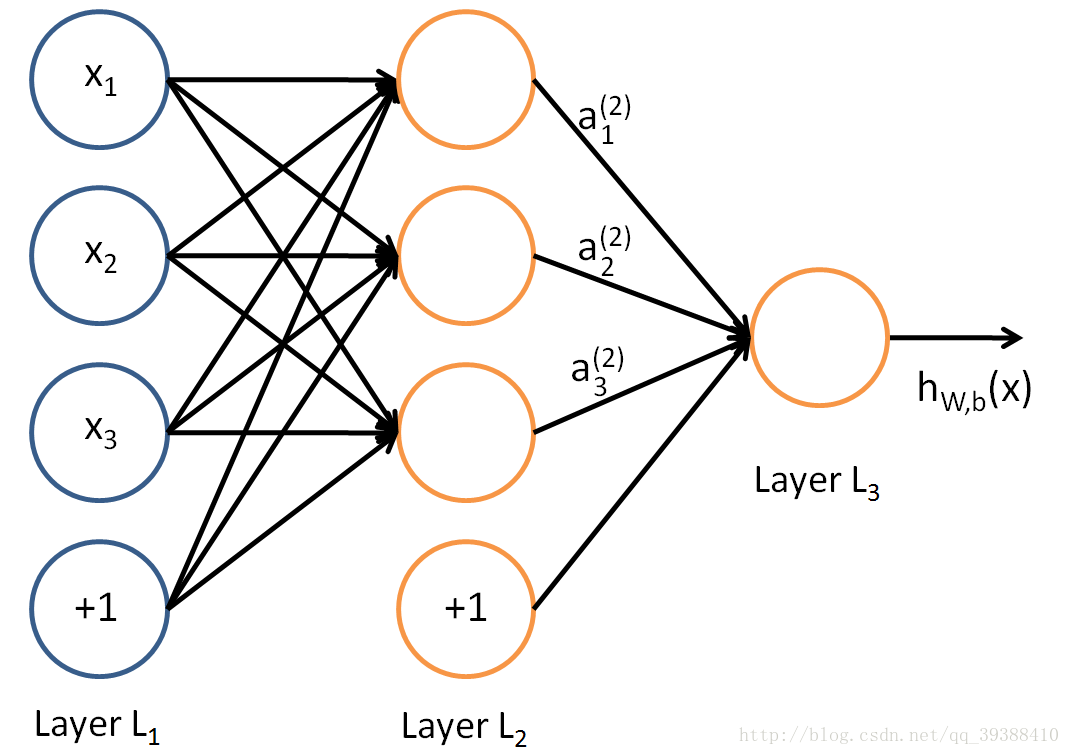
而正如模擬生物神經網路，當神經元“興奮”時就會向其相連的神經元傳送某些化學物質去改變相連神經元的電位，而且如果電位超過某個閾值（threshold），神經元將就會被啟用。事實上，不考慮它是否真的模擬了生物神經網路，只需將一個神經網路視為包含了許多引數的數學模型，由若干個函式相互巢狀即可。採用Sigmoid做啟用函式（activation function），可以構建一個多層感知機，由許多邏輯單元按照不同層級組織起來，每一層的輸出變數都是下一層的輸入變數：

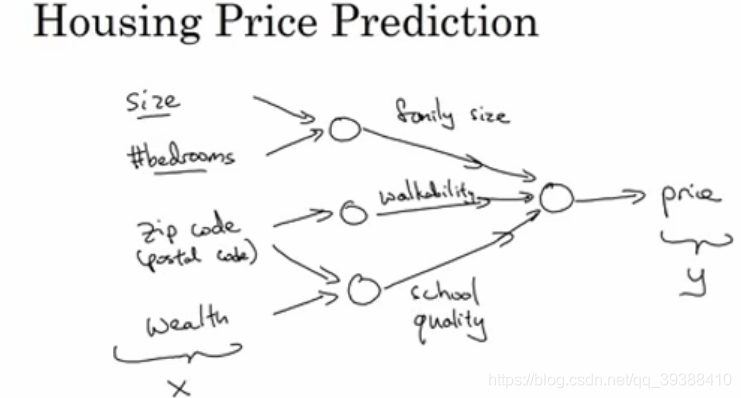
@@@實際上多層神經元是由多個線性存在級聯產生的，由低階的特徵逐步擴充套件至更抽象的描述，最終再得到想要的目標結果。

其中x1，x2，x3是輸入單元（input units），將原始資料輸入給它們。a1，a2，a3是中間單元，負責處理資料，然後呈遞到下一層，最後是輸出單元，它負責計算h（x）。然後與感知機類似，可以算出 $a_1^{(2)}= \sigma(w_{11}^{(1)}x_1 + w_{12}^{(1)}x_2 + w_{13}^{(1)}x_3 + b_1^{(1)})$
$a_2^{(2)}= \sigma(w_{21}^{(1)}x_1 + w_{22}^{(1)}x_2 + w_{23}^{(1)}x_3 + b_2^{(1)})$
$a_3^{(2)}= \sigma(w_{31}^{(1)}x_1 + w_{32}^{(1)}x_2 + w_{33}^{(1)}x_3 + b_3^{(1)})$
計算結果做下一次的輸入，然後可得：
$h_{W,b}(x)= \sigma(w_{11}^{(2)}a_1^{(2)} + w_{12}^{(2)}a_2^{(2)} + w_{13}^{(2)}a_3^{(2)} + b_1^{(2)})$
機器學習老套路，此時需要一個損失函式來微調，常見的均方誤差： $J(W,b,x,y) = \frac{1}{2}||h_{W,b}(x)-y||_2^2$
然後基於梯度下降策略，對引數們進行一層一層的誤差逆傳遞（Error BackPropagation，BP）更新引數。
$W^l = W^l -\alpha \sum\limits_{i=1}^m \delta^{i,l}(a^{i, l-1})^T$
$b^l = b^l -\alpha \sum\limits_{i=1}^m \delta^{i,l}$

相關推薦