Convolution Neural Networks(卷積神經網路大家族)
CNN原理:
受哺乳動物視覺系統的結構啟發,人們引入了一個處理圖片的強大模型結構,後來發展成了現代卷積網路的基礎。所謂卷積引自數學中的卷積運算:
它的意義在於,比如有一段時間內的股票或者其他的測量資料,顯然時間離當下越近的資料與結果越相關,作用越大,所以在處理資料時可以採用一種區域性加權平均的方法,這就叫卷積,其離散形式為:
公式中的第一個引數x是輸入的資料,第二引數w叫核函式,a表示時間t的時間間隔,而函式的輸出可以被叫做特徵對映(feature map)。也就是說完成特徵對映的過程叫卷積,不過是某一個東西和另一個東西在時間維度上的“疊加”作用。而使用卷積運算的重要作用就是,通過卷積運算,可以使原訊號特徵增強,並且降低噪音。
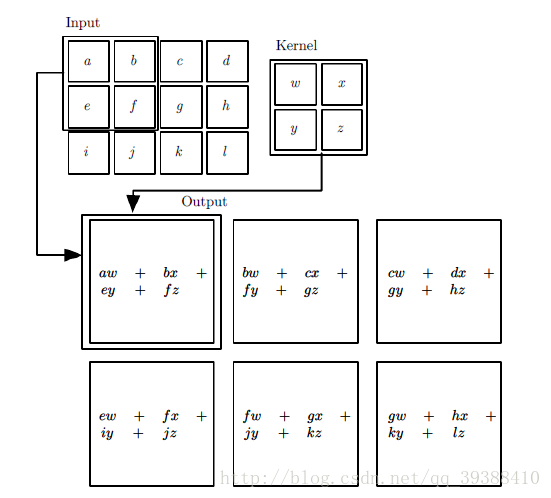
卷積神經網路裡的卷積層為:
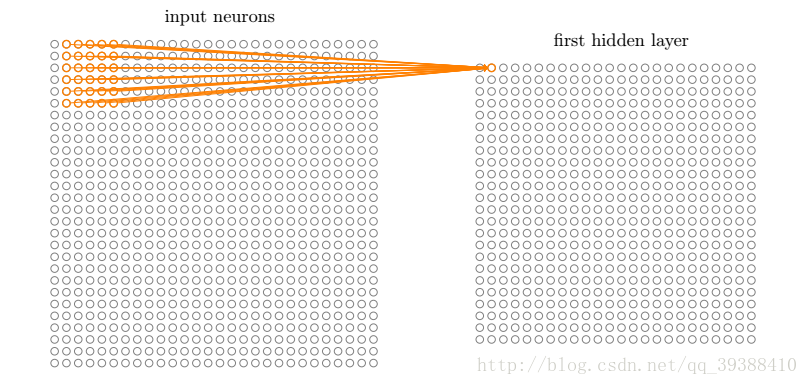
卷積過程採用了稀疏互動(Sparse interactions),引數共享(parameter sharing),等變表示(equivariant representations)三大思想。稀疏互動是利用了局部感受野(local receptive fields),限制了空間的大小,引數共享就是權值共享不但能減少引數數量,還能控制模型規模,增強模型的泛化能力。
如圖所示,卷積層的學習輸出是:
卷積神經網路裡的池化層為:
池化層也稱亞取樣層(Subsampling Layer),簡單來說,就是利用其區域性相關性,在“取樣”資料的同時還保留了有用資訊。巧妙的取樣還具備區域性線性轉換不變性(translation invariant),即如果選用連續範圍作為池化區域,並且只是池化相同的隱藏單元產生的特徵,那麼池化單元就具有平移不變性,這意味著即使影象有一個小平移,依然會產生相同的池化特徵,這種網路結構對於平移,比例縮放,傾斜,或者共他形式的變形具有高度不變性。而且使用池化可以看作是增加了一個無限強的先驗,卷積層學得的函式必須具有對少量平移的不變性,從而增強卷積神經網路的泛化處理能力,預防網路過擬合。而且這樣聚合的最直接目的是可以大大降低下一層待處理的資料量,降低了網路的複雜度,減少了引數數量。
池化函式使用某一位置的相鄰輸出的總計特徵來代替網路在該位置的輸出,常見的統計特性有最大值、均值、累加和及L2範數等。
如圖所示,池化層的輸出是:
不過在實踐中,有時可能會希望跳過核的一些位置來降低計算開銷,由此產生了步幅(stride)。
零填充(zero-padding)以獲取低維度:此操作通常用於邊界處理。因為有時候卷積核的大小並不一定剛好就被輸入資料矩陣的維度大小乘除。因此就可能會出現卷積核不能完全覆蓋邊界元素的情況,逼迫我們“二選一”。所以這時候就需要在輸入矩陣的邊緣使用零值進行填充來解決這個問題。而且通過pad操作可以更好的控制特徵圖的大小。使用零填充的卷積叫做泛卷積(wide convolution),不適用零填充的叫做嚴格卷積(narrow convolution)。
卷積神經網路裡的全連線層為:
全連線層(Fully Connected Layer,簡稱FC)。“全連線”意味著,前層網路中的所有神經元都與下一層的所有神經元連線。全連線層設計目的在於,它將前面各個層學習到的“分散式特徵表示”,對映到樣本標記空間,然後利用損失函式來調控學習過程,最後給出物件的分類預測。不同於BP全連線網路的是,卷積神經網路在輸出層使用的啟用函式不同,比如說它可能會使用Softmax函式,ReLU函式等)。
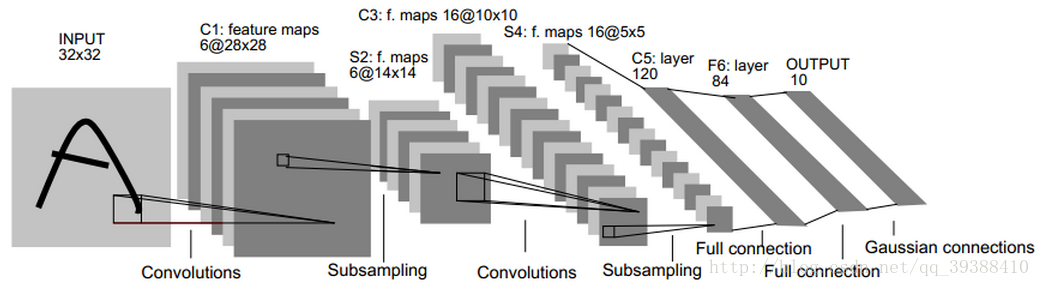
比如上圖網路的具體步驟是:
輸入為32×32的原影象。
第一層是卷積層C1,經過5×5的的感受野,有6個卷積核,形成6個28×28的特徵對映。這層的引數個數為5*5*6+6(偏置項的個數)
第二層是池化層S2,用於實現抽樣和池化平均,經過2×2的的感受野,形成6個14×14的特徵對映。這層的引數個數為[1(訓練得到的引數)+1(訓練得到的偏置項)]×6=12
第三層是卷積層C3,與第一層一樣,形成16個10×10的特徵對映。引數個數為5*5*16+16=416
第四層是池化層S4,與第二層一樣,形成16個5×5的特徵對映。引數個數為(1+1)*16=32
之後就是120個神經元,64個神經元全連線而成的全連線層,最後得到徑向基函式輸出結果。
正向傳播完成後,將結果與真實值做比較,然後極小化誤差反向調整權值矩陣。
TF應用:
CIFAR-10 資料集的分類。
引數說明:
conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None,data_format=None, name=None)
input:輸入的資料。格式為張量。[batch, in_height, in_width, in_channels]。
批次,高度,寬度,輸入通道數。
filter:卷積核。格式為[filter_height, filter_width, in_channels, out_channels]。
高度,寬度,輸入通道數,輸出通道數。
strides:步幅
padding:如果是SAME,則保留影象周圈不完全卷積的部分。VALID相反。
use_cudnn_on_gpu:是否使用cudnn加速
max_pool(value, ksize, strides, padding, data_format=“NHWC”, name=None)
value:張量,格式為[batch, height, width, channels]。
批次,高度,寬度,輸入通道數。
ksize:視窗大小
strides:步幅
padding:如果是SAME,則保留影象周圈不完全卷積的部分。VALID相反。
import tensorflow as tf
import tensorflow.examples.tutorials.mnist.input_data as input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)#下載mnist資料集
x = tf.placeholder(tf.float32, [None, 784])
y_actual = tf.placeholder(tf.float32, shape=[None, 10])
#初始化權值 W
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
#初始化偏置項 b
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
#卷積層
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
#池化層
def max_pool(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1],strides=[1, 2, 2, 1], padding='SAME')
#搭建CNN
x_image = tf.reshape(x, [-1,28,28,1])#轉換輸入資料shape
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)#第一個卷積層
h_pool1 = max_pool(h_conv1)#第一個池化層
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)#第二個卷積層
h_pool2 = max_pool(h_conv2)#第二個池化層
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)#第一個全連線層
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)#dropout
#輸出0~9的分類
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_predict=tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)#softmax啟用函式
cross_entropy = -tf.reduce_sum(y_actual*tf.log(y_predict))#交叉熵損失函式
train_step = tf.train.GradientDescentOptimizer(1e-3).minimize(cross_entropy)#梯度下降
correct_prediction = tf.equal(tf.argmax(y_predict,1), tf.argmax(y_actual,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))#計算準確度
sess=tf.InteractiveSession()#初始化
sess.run(tf.global_variables_initializer())
for i in range(20000):#記憶體小的請謹慎設定迭代次數
batch = mnist.train.next_batch(50)
if i%100 == 0:#每100次檢視程序
train_acc = accuracy.eval(feed_dict={x:batch[0], y_actual: batch[1], keep_prob: 1.0})
print ('step %d, training accuracy %g'%(i,train_acc))
train_step.run(feed_dict={x: batch[0], y_actual: batch[1], keep_prob: 0.5})
test_acc=accuracy.eval(feed_dict={x: mnist.test.images, y_actual: mnist.test.labels, keep_prob: 1.0})
print ("test accuracy %g"%test_acc)
如果用keras實現則是:
from keras import layers
from keras.models import Model
def lenet_5(in_shape=(32,32,1), n_classes=10, opt='sgd'):
in_layer = layers.Input(in_shape)
conv1 = layers.Conv2D(filters=20, kernel_size=5,
padding='same', activation='relu')(in_layer)
pool1 = layers.MaxPool2D()(conv1)
conv2 = layers.Conv2D(filters=50, kernel_size=5,
padding='same', activation='relu')(pool1)
pool2 = layers.MaxPool2D()(conv2)
flatten = layers.Flatten()(pool2)
dense1 = layers.Dense(500, activation='relu')(flatten)
preds = layers.Dense(n_classes, activation='softmax')(dense1)
model = Model(in_layer, preds)
model.compile(loss="categorical_crossentropy", optimizer=opt,
metrics=["accuracy"])
return model
if __name__ == '__main__':
model = lenet_5()
print(model.summary())
卷積只能在同一組進行嗎?– Group convolution
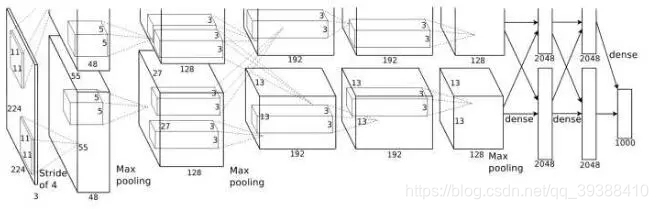
分組卷積最早在AlexNet中出現,由於當時的硬體資源有限,訓練AlexNet時卷積操作不能全部放在同一個GPU處理,因此作者把feature maps分給多個GPU分別進行處理,具體架構包括5個卷積層和3個全連線層。這八層也都採用了當時的兩個新概念——最大池化和Relu啟用來為模型提供優勢,最後把多個GPU的結果進行融合。
from keras import layers
from keras.models import Model
def alexnet(in_shape=(227,227,3), n_classes=1000, opt='sgd'):
in_layer = layers.Input(in_shape)
conv1 = layers.Conv2D(96, 11, strides=4, activation='relu')(in_layer)
pool1 = layers.MaxPool2D(3, 2)(conv1)
conv2 = layers.Conv2D(256, 5, strides=1, padding='same', activation='relu')(pool1)
pool2 = layers.MaxPool2D(3, 2)(conv2)
conv3 = layers.Conv2D(384, 3, strides=1, padding='same', activation='relu')(pool2)
conv4 = layers.Conv2D(256, 3, strides=1, padding='same', activation='relu')(conv3)
pool3 = layers.MaxPool2D(3, 2)(conv4)
flattened = layers.Flatten()(pool3)
dense1 = layers.Dense(4096, activation='relu')(flattened)
drop1 = layers.Dropout(0.5)(dense1)
dense2 = layers.Dense(4096, activation='relu')(drop1)
drop2 = layers.Dropout(0.5)(dense2)
preds = layers.Dense(n_classes, activation='softmax')(drop2)
model = Model(in_layer, preds)
model.compile(loss="categorical_crossentropy", optimizer=opt,
metrics=["accuracy"])
return model
if __name__ == '__main__':
model = alexnet()
print(model.summary())
卷積核一定越大越好?– 3×3卷積核
AlexNet中用到了一些非常大的卷積核,比如11×11、5×5卷積核,之前人們的觀念是,卷積核越大,receptive field(感受野)越大,看到的圖片資訊越多,因此獲得的特徵越好。但是大的卷積核會導致計算量的暴增,不利於模型深度的增加,計算效能也會降低。於是在VGG(最早使用,程式碼如下)、Inception網路中,利用2個3×3卷積核的組合比1個5×5卷積核的效果更佳,同時引數量(3×3×2+1 VS 5×5×1+1)被降低,因此後來3×3卷積核被廣泛應用在各種模型中。
from keras import layers
from keras.models import Model, Sequential
from functools import partial
conv3 = partial(layers.Conv2D,
kernel_size=3,
strides=1,
padding='same',
activation='relu')
def block(in_tensor, filters, n_convs):
conv_block = in_tensor
for _ in range(n_convs):
conv_block = conv3(filters=filters)(conv_block)
return conv_block
def _vgg(in_shape=(227,227,3),
n_classes=1000,
opt='sgd',
n_stages_per_blocks=[2, 2, 3, 3, 3]):
in_layer = layers.Input(in_shape)
block1 = block(in_layer, 64, n_stages_per_blocks[0])
pool1 = layers.MaxPool2D()(block1)
block2 = block(pool1, 128, n_stages_per_blocks[1])
pool2 = layers.MaxPool2D()(block2)
block3 = block(pool2, 256, n_stages_per_blocks[2])
pool3 = layers.MaxPool2D()(block3)
block4 = block(pool3, 512, n_stages_per_blocks[3])
pool4 = layers.MaxPool2D()(block4)
block5 = block(pool4, 512, n_stages_per_blocks[4])
pool5 = layers.MaxPool2D()(block5)
flattened = layers.GlobalAvgPool2D()(pool5)
dense1 = layers.Dense(4096, activation='relu')(flattened)
dense2 = layers.Dense(4096, activation='relu')(dense1)
preds = layers.Dense(1000, activation='softmax')(dense2)
model = Model(in_layer, preds)
model.compile(loss="categorical_crossentropy", optimizer=opt,
metrics=["accuracy"])
return model
def vgg16(in_shape=(227,227,3), n_classes=1000, opt='sgd'):
return _vgg(in_shape, n_classes, opt)
def vgg19(in_shape=(227,227,3), n_classes=1000, opt='sgd'):
return _vgg(in_shape, n_classes, opt, [2, 2, 4, 4, 4])
if __name__ == '__main__':
model = vgg19()
print(model.summary())
每層卷積只能用一種尺寸的卷積核?– Inception結構
傳統的層疊式網路,基本上都是一個個卷積層的堆疊,每層只用一個尺寸的卷積核,例如VGG結構中使用了大量的3×3卷積層。事實上,同一層feature map可以分別使用多個不同尺寸的卷積核,以獲得不同尺度的特徵,再把這些特徵結合起來,得到的特徵往往比使用單一卷積核的要好,谷歌的GoogleNet。但是同樣的,引數量加大,計算量會暴增。
怎樣才能減少卷積層引數量?– Bottleneck
Inception結構中加入了一些1×1的卷積核降維!
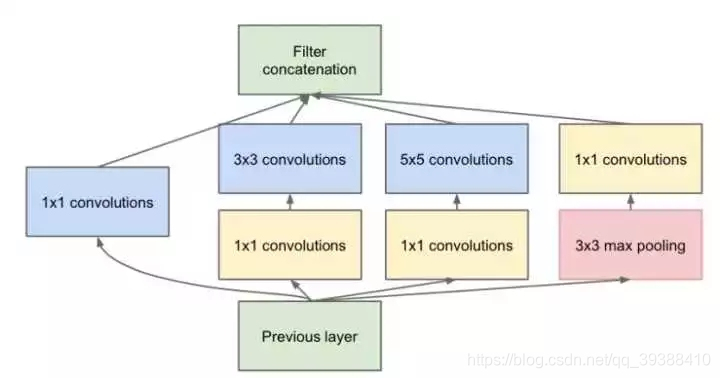
如果一個n維的直接進過3x3卷積,將會有nx3x3xn的引數(若輸出也為n維),如果在前後各加一層1x1,則會有n×1×1×(n/4) + (n/4)×3×3×(n/4) + (n/4)×1×1×n,將會大大減少引數。所以1×1卷積核也被認為是影響深遠的操作,往後大型的網路為了降低引數量都會應用上1×1卷積核。
GoogLeNet/Inception 的 架構實現如下:
from keras import layers
from keras.models import Model
from functools import partial
conv1x1 = partial(layers.Conv2D, kernel_size=1, activation='relu')
conv3x3 = partial(layers.Conv2D, kernel_size=3, padding='same', activation='relu')
conv5x5 = partial(layers.Conv2D, kernel_size=5, padding='same', activation='relu')
def inception_module(in_tensor, c1, c3_1, c3, c5_1, c5, pp):
conv1 = conv1x1(c1)(in_tensor)
conv3_1 = conv1x1(c3_1)(in_tensor)
conv3 = conv3x3(c3)(conv3_1)
conv5_1 = conv1x1(c5_1)(in_tensor)
conv5 = conv5x5(c5)(conv5_1)
pool_conv = conv1x1(pp)(in_tensor)
pool = layers.MaxPool2D(3, strides=1, padding='same')(pool_conv)
merged = layers.Concatenate(axis=-1)([conv1, conv3, conv5, pool])
return merged
def aux_clf(in_tensor):
avg_pool = layers.AvgPool2D(5, 3)(in_tensor)
conv = conv1x1(128)(avg_pool)
flattened = layers.Flatten()(conv)
dense = layers.Dense(1024, activation='relu')(flattened)
dropout = layers.Dropout(0.7)(dense)
out = layers.Dense(1000, activation='softmax')(dropout)
return out
def inception_net(in_shape=(224,224,3), n_classes=1000, opt='sgd'):
in_layer = layers.Input(in_shape)
conv1 = layers.Conv2D(64, 7, strides=2, activation='relu', padding='same')(in_layer)
pad1 = layers.ZeroPadding2D()(conv1)
pool1 = layers.MaxPool2D(3, 2)(pad1)
conv2_1 = conv1x1(64)(pool1)
conv2_2 = conv3x3(192)(conv2_1)
pad2 = layers.ZeroPadding2D()(conv2_2)
pool2 = layers.MaxPool2D(3, 2)(pad2)
inception3a = inception_module(pool2, 64, 96, 128, 16, 32, 32)
inception3b = inception_module(inception3a, 128, 128, 192, 32, 96, 64)
pad3 = layers.ZeroPadding2D()(inception3b)
pool3 = layers.MaxPool2D(3, 2)(pad3)
inception4a = inception_module(pool3, 192, 96, 208, 16, 48, 64)
inception4b = inception_module(inception4a, 160, 112, 224, 24, 64, 64)
inception4c = inception_module(inception4b, 128, 128, 256, 24, 64, 64)
inception4d = inception_module(inception4c, 112, 144, 288, 32, 48, 64)
inception4e = inception_module(inception4d, 256, 160, 320, 32, 128, 128)
pad4 = layers.ZeroPadding2D()(inception4e)
pool4 = layers.MaxPool2D(3, 2)(pad4)
aux_clf1 = aux_clf(inception4a)
aux_clf2 = aux_clf(inception4d)
inception5a = inception_module(pool4, 256, 160, 320, 32, 128, 128)
inception5b = inception_module(inception5a, 384, 192, 384, 48, 128, 128)
pad5 = layers.ZeroPadding2D()(inception5b)
pool5 = layers.MaxPool2D(3, 2)(pad5)
avg_pool = layers.GlobalAvgPool2D()(pool5)
dropout = layers.Dropout(0.4)(avg_pool)
preds = layers.Dense(1000, activation='softmax')(dropout)
model = Model(in_layer, [preds, aux_clf1, aux_clf2])
model.compile(loss="categorical_crossentropy", optimizer=opt,
metrics=["accuracy"])
return model
if __name__ == '__main__':
model = inception_net()
print(model.summary())
越深的網路就越難訓練嗎?– Resnet殘差網路
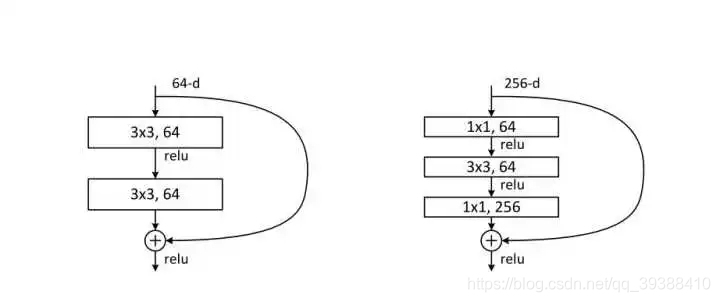
傳統的卷積層層疊網路會遇到一個問題,當層數加深時,網路的表現越來越差,很大程度上的原因是因為當層數加深時,梯度消失得越來越嚴重,以至於反向傳播很難訓練到淺層的網路。直接對映是很難學習的,所以不去學習網路輸出層與輸入層間的對映,而是學習它們之間的差異——殘差。下面是殘差網路的實現:
from keras import layers
from keras.models import Model
def _after_conv(in_tensor):
norm = layers.BatchNormalization()(in_tensor)
return layers.Activation('relu')(norm)
def conv1(in_tensor, filters):
conv = layers.Conv2D(filters, kernel_size=1, strides=1)(in_tensor)
return _after_conv(conv)
def conv1_downsample(in_tensor, filters):
conv = layers.Conv2D(filters, kernel_size=1, strides=2)(in_tensor)
return _after_conv(conv)
def conv3(in_tensor, filters):
conv = layers.Conv2D(filters, kernel_size=3, strides=1, padding='same')(in_tensor)
return _after_conv(conv)
def conv3_downsample(in_tensor, filters):
conv = layers.Conv2D(filters, kernel_size=3, strides=2, padding='same')(in_tensor)
return _after_conv(conv)
def resnet_block_wo_bottlneck(in_tensor, filters, downsample=False):
if downsample:
conv1_rb = conv3_downsample(in_tensor, filters)
else:
conv1_rb = conv3(in_tensor, filters)
conv2_rb = conv3(conv1_rb, filters)
if downsample:
in_tensor = conv1_downsample(in_tensor, filters)
result = layers.Add()([conv2_rb, in_tensor])
return layers.Activation('relu')(result)
def resnet_block_w_bottlneck(in_tensor,
filters,
downsample=False,
change_channels=False):
if downsample:
conv1_rb = conv1_downsample(in_tensor, int(filters/4))
else:
conv1_rb = conv1(in_tensor, int(filters/4))
conv2_rb = conv3(conv1_rb, int(filters/4))
conv3_rb = conv1(conv2_rb, filters)
if downsample:
in_tensor = conv1_downsample(in_tensor, filters)
elif change_channels:
in_tensor = conv1(in_tensor, filters)
result = layers.Add()([conv3_rb, in_tensor])
return result
def _pre_res_blocks(in_tensor):
conv = layers.Conv2D(64, 7, strides=2, padding='same')(in_tensor)
conv = _after_conv(conv)
pool = layers.MaxPool2D(3, 2, padding='same')(conv)
return pool
def _post_res_blocks(in_tensor, n_classes):
pool = layers.GlobalAvgPool2D()(in_tensor)
preds = layers.Dense(n_classes, activation='softmax')(pool)
return preds
def convx_wo_bottleneck(in_tensor, filters, n_times, downsample_1=False):
res = in_tensor
for i in range(n_times):
if i == 0:
res = resnet_block_wo_bottlneck(res, filters, downsample_1)
else:
res = resnet_block_wo_bottlneck(res, filters)
return res
def convx_w_bottleneck(in_tensor, filters, n_times, downsample_1=False):
res = in_tensor
for i in range(n_times):
if i == 0:
res = resnet_block_w_bottlneck(res, filters, downsample_1, not downsample_1)
else:
res = resnet_block_w_bottlneck(res, filters)
return res
def _resnet(in_shape=(224,224,3),
n_classes=1000,
opt='sgd',
convx=[64, 128, 256, 512],
n_convx=[2, 2, 2, 2],
convx_fn=convx_wo_bottleneck):
in_layer = layers.Input(in_shape)
downsampled = _pre_res_blocks(in_layer)
conv2x = convx_fn(downsampled, convx[0], n_convx[0])
conv3x = convx_fn(conv2x, convx[1], n_convx[1], True)
conv4x = convx_fn(conv3x, convx[2], n_convx[2], True)
conv5x = convx_fn(conv4x, convx[3], n_convx[3], True)
preds = _post_res_blocks(conv5x, n_classes)
model = Model(in_layer, preds)
model.compile(loss="categorical_crossentropy", optimizer=opt,
metrics=["accuracy"])
return model
def resnet18(in_shape=(224,224,3), n_classes=1000, opt='sgd'):
return _resnet(in_shape, n_classes, opt)
def resnet34(in_shape=(224,224,3), n_classes=1000, opt='sgd'):
return _resnet(in_shape,
n_classes,
opt,
n_convx=[3, 4, 6, 3])
def resnet50(in_shape=(224,224,3), n_classes=1000, opt='sgd'):
return _resnet(in_shape,
n_classes,
opt,
[256, 512, 1024, 2048],
[3, 4, 6, 3],
convx_w_bottleneck)
def resnet101(in_shape=(224,224,3), n_classes=1000, opt='sgd'):
return _resnet(in_shape,
n_classes,
opt,
[256, 512, 1024, 2048],
[3, 4, 23, 3],
convx_w_bottleneck)
def resnet152(in_shape=(224,224,3), n_classes=1000, opt='sgd'):
return _resnet(in_shape,
n_classes,
opt,
[256, 512, 1024, 2048],
[3, 8, 36, 3],
convx_w_bottleneck)
if __name__ == '__main__':
model = resnet50()
print(model.summary())
卷積操作時必須同時考慮通道和區域嗎?– DepthWise操作
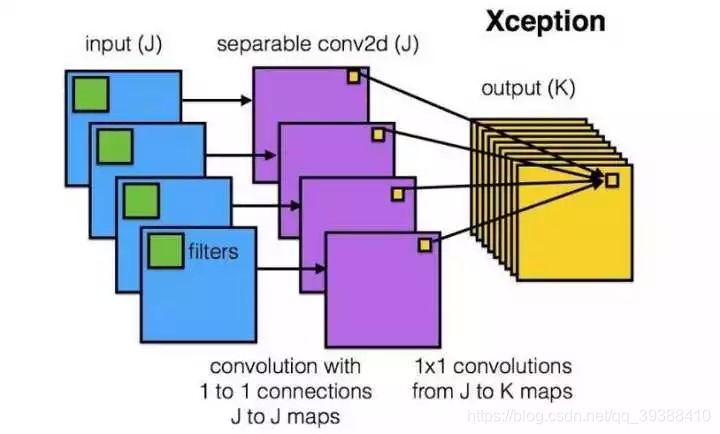
DW:首先對每一個通道進行各自的卷積操作,有多少個通道就有多少個過濾器。得到新的通道feature maps之後,這時再對這批新的通道feature maps進行標準的1×1跨通道卷積操作。
如果直接一個3×3×256的卷積核,引數量為:3×3×3×256(通道數為3,輸出為256),DW的引數量為:3×3×3 + 3×1×1×256,又再次大大減少了引數量。
分組卷積能否對通道進行隨機分組?– ShuffleNet
通道間的特徵都是平等的嗎? – SEnet
能否讓固定大小的卷積核看到更大範圍的區域?– Dilated convolution
卷積核大小依然是3×3,但是每個卷積點之間有1個空洞,也就是在綠色7×7區域裡面,只有9個紅色點位置作了卷積處理,其餘點權重為0。這樣即使卷積核大小不變,但它看到的區域變得更大了。
卷積核形狀一定是矩形嗎?– Deformable convolution 可變形卷積核
直接在原來的過濾器前面再加一層過濾器,這層過濾器學習的是下一層卷積核的位置偏移量(offset)。變形的卷積核能讓它只看感興趣的影象區域 ,這樣識別出來的特徵更佳。
主要參考:
bengio deep learning
深度思考·DeepThinking
Faisal Shahbaz Five Powerful CNN Architectures