【LeetCode & 劍指offer刷題】動態規劃與貪婪法題9:Unique Paths(系列)
阿新 • • 發佈:2019-01-06
【LeetCode & 劍指offer 刷題筆記】目錄(持續更新中...)
Unique Paths(系列)
Unique Paths A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below). The robot can only move either down or right a
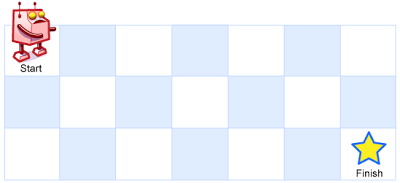
Above is a 7 x 3 grid. How many possible unique paths are there?
C++ //問題:街區路徑問題(與LCS最長公共子序列問題類似) 求機器人從起點到終點的路徑數量 //方法一:設P[i][j] 為到座標(i,j)的路徑總數,則由於機器人 只能向右或者向下 ,故有P[i][j] = P[i - 1][j] + P[i][j - 1] //O(n^2) O(m*n) class Solution { public : int uniquePaths ( int m , int n ) { vector < vector < int >> path ( m , vector < int >( n , 1 )); //(1,0)和(0,1)處初始化為1 for ( int i = 1 ; i < m ; i ++) //i從1開始,掃描行 for ( int j = 1 ; j < n ; j ++) //掃描列 path [i][j] = path[i-1][j] + path[i][j-1]; return path [ m - 1 ][ n - 1 ]; } }; /* * 方法一改進 用一個列向量存當前需要的元素即可,將空間複雜度優化至O(min(m,n)) * 例子 1 1 1 1 1 1 1 2 3 4 5 6 1 3 6 10 15 21 dp[i][j] = dp[i - 1][j] + dp[i][j - 1] dp[i][j],dp[i-1][j] ---> dp[j] dp[i][j-1] ---> dp[j-1] */ class Solution { public : int uniquePaths ( int m , int n ) { vector < int > dp ( n , 1 ); //進一步改進可以選擇min(m,n) for ( int i = 1 ; i < m ; ++ i ) //掃描行 { for ( int j = 1 ; j < n ; ++ j ) //掃描列 { dp [ j ] += dp [ j - 1 ]; } } return dp [ n - 1 ]; } }; 63 . Unique Paths II Now consider if some obstacles are added to the grids. How many unique paths would there be? An obstacle and empty space is marked as 1 and 0 respectively in the grid. Note: m and n will be at most 100. Example 1: Input: [ [0,0,0], [0,1,0], [0,0,0] ] Output: 2 Explanation: There is one obstacle in the middle of the 3x3 grid above. There are two ways to reach the bottom-right corner: 1. Right -> Right -> Down -> Down 2. Down -> Down -> Right -> Right
/* 問題:有障礙物的柵格中,機器人從起始點到終點的路徑數量 方法:動態規劃 對於有障礙物的柵格中,dp值置0 */ class Solution { public : int uniquePathsWithObstacles ( vector < vector < int >>& obstacleGrid ) { if ( obstacleGrid . empty () || obstacleGrid [ 0 ]. empty () || obstacleGrid [ 0 ][ 0 ] == 1 ) return 0 ; //矩陣為空或者起始點為障礙點時,退出 int m = obstacleGrid . size (); int n = obstacleGrid [ 0 ]. size (); vector < vector < int >> dp ( m , vector < int >( n )); //初始化為0 for ( int i = 0 ; i < m ; i ++) //從0開始掃描,因為任何點都有可能為障礙點(如(0,1)和(1,0)) { for ( int j = 0 ; j < n ; j ++) { if ( obstacleGrid [ i ][ j ] == 1 ) dp [ i ][ j ] = 0 ; //有障礙的地方dp值置0 else if ( i == 0 && j == 0 ) dp [ i ][ j ] = 1 ; //起始點到起始點路徑數為1(若無障礙) else if ( i == 0 && j > 0 ) dp [ i ][ j ] = dp [ i ][ j - 1 ]; //第一行的處理 else if ( i > 0 && j == 0 ) dp [ i ][ j ] = dp [ i - 1 ][ j ]; //第一列的處理 else dp [ i ][ j ] = dp [ i - 1 ][ j ] + dp [ i ][ j - 1 ]; //其他情況的處理 } } return dp . back (). back (); //返回末尾點 } };
