目錄

• 高冷貴族: 隱馬爾可夫模型
  • 引言
  • 例子
  • 描述模型
  • 基本概念*
    • 定義
    • 基本假設
    • 基本問題
  • 前向,後向演算法
    • 前向演算法
    • 後向演算法
    • 舉例計算
  • 學習問題
    • 已知觀測序列及隱序列
    • 已知觀測序列
  • 預測問題
    • Viterbi 演算法
    • 舉例計算
  • 昇華
  • 參考文獻

高冷貴族: 隱馬爾可夫模型

引言

大家都用過Siri,Cortana之類的語音助手吧? 當你對著手機說出'我的女朋友溫柔嗎?',Siri 或Cortana就會根據你說的這句話翻譯成一段文字,然後再作應答. 先不管應答部分, 你可曾想過: Siri是如何將你說的話翻譯成一段文字的?嗯,猜對了, 這裡就用到了隱馬爾可夫模型(Hiden Markov Model, HMM).

例子

假設你有三個女朋友(嘿~,現實不可以,想想總可以吧~,/躲拖鞋…), 你每週末只能選擇陪其中一位(為了世界和平…). 而作為程式設計師的你,也沒有什麼情調,只會與女朋友做二種事情: 吃飯,看電影, 而因為工作繁忙,你每週也只能做其中一件事,三位美麗的女士也很理解,體諒你,也都很配合,很高興.

那麼問題來了, 你是如何選擇週末去陪哪個女朋友呢? 三位女士都很可愛,你不想冷落每一個人,但第一個女朋友(記為A女朋友)有點聒噪,因此你會稍微少去一點她那裡. 第二,第三個女朋友去都比較安靜(分別記為B,C). 於是,你在心裡默默地(或者是潛意識地)定下了去陪三位女朋友的概率:

女朋友	A	B	C
概率	0.2	0.4	0.4

比如,陪A女朋友的概率是0.2,可簡單的理解為十次大約有二次會去陪她. 然而這只是你剛開始考慮的事,因為當你週末陪女朋友結束之後,你會根據本次的約會體驗選擇下一週要陪伴的女朋友.之前初始的'選擇'概率就不再起作用了.

那約會結束後你是如何選擇下一週的女士呢? 因為三位女士的性格比較穩定,因此每次的體驗都會差不多,於是你的內心又有了一個下週去哪個女朋友的概率了:

本週陪伴\下週陪伴	A	B	C
A	0.5	0.2	0.3
B	0.3	0.5	0.2
C	0.2	0.3	0.5

什麼意思呢? 比如你本週陪伴A了,那下週你繼續陪A的概率是0.5, 而下週去陪B的概率則為0.2, 而去陪伴C的為0.3.

還沒完~, 因為每個女朋友的喜好不一樣,因此你們在一起做的事也不一樣: A比較隨意,吃飯,看電影都可沒,沒差; B比較文藝,則喜歡看電影會稍微多一些; C 則是個吃貨,比較喜歡吃飯,但也會看電影.於是,你的心裡又有譜了:

女朋友	吃飯	看電影
A	0.5	0.5
B	0.4	0.6
C	0.7	0.3

也就是說,比如對於C來說, 你們在一起呢,0.7的概率會去吃飯,也即十次大約有7次會去吃飯, 而有約三次會去看電影.

有一天,你在朋友圈發了個狀態: 吃,吃,看,看,吃.

這引起了你朋友圈的三個人的興趣:

你老媽, 你老媽對你的情況比較瞭解,她知道你對這三位女朋友的想法(即知道上面三張表), 她現在比較感興趣的是,下週她兒子去幹嘛(也比較八卦~).

你表姐, 你表姐因為住在另一個城市,所以溝通比較少,因而你對三位女朋友的感覺(上面三張表)她並不知道,只知道你同時和三位女生談戀愛,所以她現在想根據你的發出的狀態判斷出你對三位女生的感覺(上面三張表).

你同事, 你同事也是你的基友,因此對你的事比較瞭解,沒事你會跟說說三個女生在你心裡的感受(上面三張表),但為防止他八卦,你並沒有把每週去哪位女朋友那裡告訴他.這下可勾起了他的好奇心,於是想根據你的狀態猜出你每週都是陪伴的誰.

好了,隱馬爾可夫模型講完了~

什麼? Are you kidding me ?

沒有,真的,這就是馬爾可夫模型. 下面個圖來表示下.

描述模型

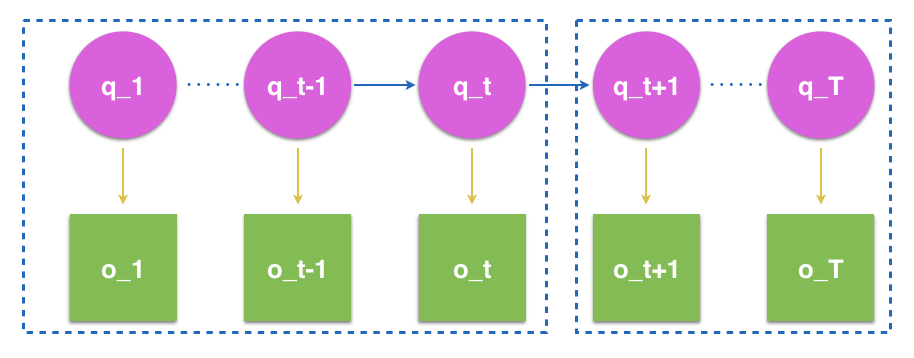
這張圖表示的就是你這五週以來與女朋友們的互動情況. 在隱馬爾可夫模型中, 粉色圈圈那一行代表的是女朋友的情況,從微信狀態的角度,它是一個隱藏在後面的狀態(沒有發在狀態裡啊~). 因此稱為(隱)狀態序列(這就是HMM中'隱'字的意思),而且這個狀態鏈呢麼是一個馬爾可夫模型或叫做馬爾可夫鏈. 什麼是馬爾可夫鏈? 就是說當前狀態只決定於前一個狀態. 在本本例中,你本週去哪個女朋友那裡,完全由你上週在哪個女朋友那裡來決定. 而綠色框框則被稱為觀測序列, 即別人從朋友圈能看到你什麼都做了什麼.

上面的三張表,即是描述模型的變數,第一張表我們稱為初始狀態向量,第二張表稱為轉移概率矩陣,第三張表則是觀測概率矩陣.

而後面三個人的想要知道的東西就是HMM的三個基本問題:概率計算問題,學習問題,以及預測問題.

(三個問題的求解方式在後面~~~)

HMM 應用非常廣泛,特別是在自然語言處理,語音識別,訊號處理,生物序列分析(DNA, 蛋白質等)等等大放異彩.HMM是時間序列模型,處理時間序列是其本職工作.

PS: 一如既往, 只做瞭解的,讀到這裡就可停下了,想深入一些的,請繼續~

基本概念*

HMM是一個時序概率模型,描述由一個隱藏的馬爾可夫鏈隨機生成不可觀測的狀態隨機序列,再由各個狀態生成一個觀測而產生觀測隨機序列的過程.具體請看上圖.

現在咱們一般化地討論一下, 設:

 

(y1,y2,…,yn),(x1,x2,…,xn)(y1,y2,…,yn),(x1,x2,…,xn)

分別為狀態序列與觀測序列, 因狀態序列是一個馬爾可夫鏈,故 所有變數的聯合概率分佈為:

P(x1,y1,…,xn,yn)=P(y1)P(x1|y1)Πni=2P(yi|yi−1)P(xi|yi)P(x1,y1,…,xn,yn)=P(y1)P(x1|y1)Πi=2nP(yi|yi−1)P(xi|yi)

欲得到聯合概率分佈,其需要右邊三個部分,P(y1)P(x1|y1)P(y1)P(x1|y1) 為初始條件; P(yi|yi−1)P(yi|yi−1) 為轉移條件; P(xi|yi)P(xi|yi) 則為觀測條件. 因此,

設:

Q 是所有可能的狀態集合, V 是所有可能的觀測集合.

 

Q={q1,q2,…,qN},V={v1,v2,…,vM}Q={q1,q2,…,qN},V={v1,v2,…,vM}

其中,N 是所有可能的狀態數, M 是所有可能的觀測數.

I 是長度為T 的狀態序列, O 是對應的觀測序列:

 

I={i1,i2,…,iT}O=(o1,o2,…,oT)I={i1,i2,…,iT}O=(o1,o2,…,oT)

A 是狀態轉移概率矩陣:

A=[aij]NXNA=[aij]NXN

其中,

aij=P(ii+1=qj|it=qi),i=1,2,…,N,j=1,2,…,Naij=P(ii+1=qj|it=qi),i=1,2,…,N,j=1,2,…,N

是在 t 時刻 處於狀態 qi 的條件下在 時間 t+1 轉移到狀態 qj 的概率.

B 是觀測概率矩陣

 

B[bj(k)]NXMB[bj(k)]NXM

其中

bj(k)=P(ot=vk|it=qj),k=1,2,…,M,j=1,2,…,Nbj(k)=P(ot=vk|it=qj),k=1,2,…,M,j=1,2,…,N

是在 t 時刻 處於狀態 q_j 的條件下生成觀測數 vk 的概率.

ππ 是初始狀態概率向量

 

π=(πi)π=(πi)

其中

πi=P(i1=qi),i=1,2,…,Nπi=P(i1=qi),i=1,2,…,N

是時刻 t = 1處於狀態 qi 概率.

有了上述準確, HMM就基本上搞定了:

定義

 

λ=(A,B,π)λ=(A,B,π)

這就是HMM,其中括號內的三個部分稱為HMM三元素.

基本假設

1. 齊次馬爾可夫性假設, 即假設 在任意時刻 t 的狀態 只有前一狀態有關,與其他任何狀態,觀測都無關:

    

   P(it|it−1,ot−1,…,i1,o1)=P(it|it−1)P(it|it−1,ot−1,…,i1,o1)=P(it|it−1)

2. 觀測獨立性假設, 即假設任意時刻的觀測 只與該時刻的馬爾可夫鏈狀態有關,與其他任何時刻狀態,觀測都無關:

    

   P(ot|iT,oT,,˙it+1,ot+1,it−1,ot−1,…,i1,o1)=P(ot|it)P(ot|iT,oT,,˙it+1,ot+1,it−1,ot−1,…,i1,o1)=P(ot|it)

基本問題

1. 概率計算問題, 給定定 λ=(A,B,π)λ=(A,B,π) 和觀測序列O=(o1,o2,…,oT)O=(o1,o2,…,oT) , 計算在模型 λλ 下 觀測序列 O 出現的概率P(O|λ)P(O|λ), 也可說是HMM與觀測的匹配程度.
2. 學習問題, 給定觀測序列 O=(o1,o2,…,oT)O=(o1,o2,…,oT) ,估計模型 λ=(A,B,π)λ=(A,B,π) 使得在該模型下, P(O|λ)P(O|λ) 最大.
3. 預測問題,也稱解碼問題, 給定定 λ=(A,B,π)λ=(A,B,π) 和觀測序列O=(o1,o2,…,oT)O=(o1,o2,…,oT) , 求使 P(O|λ)P(O|λ) 最大的狀態序列 I=(i1,i2,…,iT)I=(i1,i2,…,iT),即最有可能的狀態序列.

接下來,對於這三個問題,我們將各個擊破.

前向,後向演算法

對於第一個問題, 最簡單的方法就是暴力計算,把每種情況都考慮一遍, 不用我說,你也知道這不可行. 倒不是因為複雜,是因為算不起,它的時間複雜度是恐怖的 O(TNT)O(TNT) .

不過還真有比較不錯的演算法,而且還有兩種!

上圖可表示為一HMM列.左,右兩邊虛線內我們分別用αt(j),βt(j)αt(j),βt(j)來表示,其中

 

αt(j)=P(o1,o2,…,ot,it=qj|λ);βt(j)=P(ot+1,ot+2,…,oT|it=qj,λ)αt(j)=P(o1,o2,…,ot,it=qj|λ);βt(j)=P(ot+1,ot+2,…,oT|it=qj,λ)

這兩個就是我們分別用於前向,後向演算法的關鍵因子.

再明確一下,我們的目標是求解 P(O|λ)P(O|λ) .

前向演算法

1. 初始狀態 o1o1, 考慮出現o1o1 概率:

    

   P(o1|λ)=∑j=1NP(o1,i1=qj|λ)=∑j=1Nα1(j)=∑j=1Nπjbj(o1)P(o1|λ)=∑j=1NP(o1,i1=qj|λ)=∑j=1Nα1(j)=∑j=1Nπjbj(o1)

   
   ​

2. 當得到 P(o1,o2,…,ot|λ)P(o1,o2,…,ot|λ) , 現在要求P(o1,o2,…,ot,ot+1|λ)P(o1,o2,…,ot,ot+1|λ) ,可以先從αt+1(j)αt+1(j) 出發:

 

αt+1(j)=====P(o1,o2,…,ot,ot+1,it+1=qj|λ)∑Nk=1P(o1,o2,…,ot,ot+1,it+1=qj,it=qk|λ)∑Nk=1P(o1,o2,…,ot,it=qj|λ)ajkbj(ot+1)∑Nk=1αt(j)ajkbk(ot+1)bj(ot+1)∑Nk=1αt(j)ajkαt+1(j)=P(o1,o2,…,ot,ot+1,it+1=qj|λ)=∑k=1NP(o1,o2,…,ot,ot+1,it+1=qj,it=qk|λ)=∑k=1NP(o1,o2,…,ot,it=qj|λ)ajkbj(ot+1)=∑k=1Nαt(j)ajkbk(ot+1)=bj(ot+1)∑k=1Nαt(j)ajk

而:

 

P(o1,o2,…,ot,ot+1|λ)=∑j=1Nαt+1(j)P(o1,o2,…,ot,ot+1|λ)=∑j=1Nαt+1(j)

1. 最終:

 

P(O|λ)=∑j=1NαT(j)P(O|λ)=∑j=1NαT(j)

這就是前向演算法.

後向演算法

前向演算法是從前向後, 後向演算法則是從後向前的. 回顧:

 

βt(j)=P(ot+1,ot+2,…,oT|it=qj,λ)βt(j)=P(ot+1,ot+2,…,oT|it=qj,λ)

1. 第一步,由 ββ 定義,可知 當t = T時,

    

   βT(j)=1βT(j)=1

   
   也就是說,目前的觀測序列到時刻T,而βTβT 則關注的是 T+1 時刻, 這從現有已知條件中,對T+1 時刻沒有任何限制的,即oT+1oT+1 的任何取值都可接受,顯然在這情況下, 上式(概率)值為1.

2. 當已知 t+1時刻, 推導 t 時刻:

    

   βt(j)====P(ot+1,ot+2,…,oT|it=qj,λ)∑Nk=1P(ot+2,…,oT|ot,it=qj,it+1=qk,λ)∑Nk=1P(ot+2,…,oT|it+1=qk,λ)ajkbk(ot+1)∑Nk=1ajkbk(ot+1)βt+1(j)βt(j)=P(ot+1,ot+2,…,oT|it=qj,λ)=∑k=1NP(ot+2,…,oT|ot,it=qj,it+1=qk,λ)=∑k=1NP(ot+2,…,oT|it+1=qk,λ)ajkbk(ot+1)=∑k=1Najkbk(ot+1)βt+1(j)

3. 因此:

    

   P(O|λ)=∑j=1Nπjbj(o1)β1(j)P(O|λ)=∑j=1Nπjbj(o1)β1(j)

舉例計算

現在咱們來計算上面'三個女朋友'的例子,老媽想知道的問題. 現在我們簡化一下問題,你的微信狀態變成'吃,看,吃'. 計算方式一模一樣,只是簡化了一點,方便我行文. 這裡要計算的是'吃,看,吃'的概率正常應該是多少(有些人可能要疑惑:這個跟大媽的問題不太一樣啊~,其實是一樣的, 因為我們可以假設這'吃,看,吃'與下週出現的活動組成一個序列,並求出概率,概率最大的情況,就是你下週最有可能的活動:

前向計算

概率上面三個表:

1. 初始狀態

 

α1(1)=π1b1(o1)=0.2∗0.5=0.1α1(2)=π2b2(o1)=0.4∗0.4=0.16α1(3)=π1b3(o1)=0.4∗0.7=0.28α1(1)=π1b1(o1)=0.2∗0.5=0.1α1(2)=π2b2(o1)=0.4∗0.4=0.16α1(3)=π1b3(o1)=0.4∗0.7=0.28

1. 遞推計算

    

   α2(1)=[∑3i=1α1(i)ai1]b1(o2)=0.154∗0.5=0.077α2(1)=[∑i=13α1(i)ai1]b1(o2)=0.154∗0.5=0.077

   
   同理可演算法其他,這裡就不全寫了,

2. 最後

    

   P(O|λ)=∑i=1Na3(i)=0.13022P(O|λ)=∑i=1Na3(i)=0.13022

   
   ​

後向計算

1. β3(j)=1β3(j)=1

2. 遞推計算:

    

   β2(1)=∑j=13ai1bi(o3)β3(1)=0.51β2(1)=∑j=13ai1bi(o3)β3(1)=0.51

   
   其他同理.

3. 最終: P(O|λ)=∑3i=1πibi(o1)β1(i)=0.13022P(O|λ)=∑i=13πibi(o1)β1(i)=0.13022

前向,後向演算法結果是一樣的!

至此,第一個問題解決了. 這個問題可以用於時間序列預測問題,應用方式同上.

學習問題

有時我們並不知道HMM模型的具體形態,因此需要一些手段得到它.

在做此類問題時也可大致分為兩種情:

已知觀測序列及隱序列

這裡了也必須已知,N 是所有可能的狀態數, M 是所有可能的觀測數.

比如,對於中文分詞,我們手上有資料集, 而且我們可以很容易地定義每個字隱狀態(隱狀態: 起始字,中間字,終止字,及獨立字等等),這樣, 在兩序列已知的情況下,根據大數定律,應用最大似然求出各狀態轉移矩陣,觀測矩陣及一個初始向量.

已知觀測序列

這裡了也必須已知,N 是所有可能的狀態數, M 是所有可能的觀測數.

這裡的方法就是 EM 演算法, 不過因為在HMM中,因此有個別名叫 Baum-Welch 演算法.

預測問題

第三個問題是預測問題.預測的是給定觀測序列,背後最有可能的馬爾可夫鏈.

這個問題目前有兩種方法,第一種稱為近似演算法.此演算法尋找各個時刻的最優解,最後連成一列. 為什麼會被稱為近似演算法? 因為這樣得到的每個時刻的最優,最終並不一定是整個序列的最優解.

因此目前最好的方法是維特比(Viterbi)演算法.

Viterbi 演算法

此演算法是用動態規劃的方式解決HMM的預測問題.即把隱狀態列看成是最優路徑上的每一步,找最大概率路徑,即轉化成尋找最優路徑.

在動態規劃中, 最優路徑具有這樣的特性: 最優路徑在 t 時刻通過 結點 i, 那麼 這一路徑對於從 i 到 最後的剩餘路徑也是最優的.否則必有另一路徑比此更優,這是矛盾的.基於此 Viterbi 演算法 遞推的計算在 t 時刻的最優路徑,直至最後.根據最後的最優路徑反向確定最優路徑上的各點隱狀態.

設 t 時刻的最優路徑是

 

δt(j)=maxi1,i2,…,it−1P(it=qj,it−1,…,i1,ot,…,o1|λ),j=1,2,…,Nδt(j)=maxi1,i2,…,it−1P(it=qj,it−1,…,i1,ot,…,o1|λ),j=1,2,…,N

於是

δt+1(k)==maxi1,i2,…,itP(it=qj,it−1,…,i1,ot,…,o1|λ)max1≤j≤N[δt(j)ajk]bk(ot+1)δt+1(k)=maxi1,i2,…,itP(it=qj,it−1,…,i1,ot,…,o1|λ)=max1≤j≤N[δt(j)ajk]bk(ot+1)

這樣,

1. 最初狀態:

    

   δ1(j)=πjbj(o1)δ1(j)=πjbj(o1)

2. 已知 δt(j)δt(j) 遞推 δt+1(k)δt+1(k)

    

   δt+1(k)=max1≤j≤N[δt(j)ajk]bk(ot+1)δt+1(k)=max1≤j≤N[δt(j)ajk]bk(ot+1)

3. 最後狀態,得到全域性最優路徑

    

   pathbest=max1≤j≤NδT(j)pathbest=max1≤j≤NδT(j)

4. 反向推導 最優隱狀態序列, 令在 t+1 時刻 狀態在qkqk 的最優路徑中,第 t 個結點:

    

   ψt+1(k)=argmax1≤j≤N[δt(j)ajk]ψt+1(k)=arg⁡max1≤j≤N[δt(j)ajk]

   
   於是最終列:

   k∗1,k∗2,…,k∗Tk1∗,k2∗,…,kT∗

   
   其中

   k∗t=ψt+1(j)kt∗=ψt+1(j)

舉例計算

還是'三個女朋友的例子',還是'吃,看,吃',

首先,

 

δ1(1)=0.1,δ1(2)=0.16,δ1(3)=0.28δ1(1)=0.1,δ1(2)=0.16,δ1(3)=0.28

遞推 t = 2,

δ2(1)=max1≤j≤3[δ1(j)aj1]b1(o2)=0.028δ2(1)=max1≤j≤3[δ1(j)aj1]b1(o2)=0.028

同理:

δ2(2)=0.0504,δ2(3)=0.042δ3(1)=0.00756,δ3(2)=0.01008,δ3(3)=0.0147δ2(2)=0.0504,δ2(3)=0.042δ3(1)=0.00756,δ3(2)=0.01008,δ3(3)=0.0147

最終狀態:

pathbest=max1≤j≤3δ3(j)=0.0147pathbest=max1≤j≤3δ3(j)=0.0147

即 i3=3i3=3

反向推斷:

 

i2=ψ2+1(3)=argmax1≤j≤N[δ2(j)aj3]=3i2=ψ2+1(3)=arg⁡max1≤j≤N[δ2(j)aj3]=3

最後

i1=ψ1+1(3)=argmax1≤j≤N[δt(j)aj3]=3i1=ψ1+1(3)=arg⁡max1≤j≤N[δt(j)aj3]=3

因此最終狀態[3,3,3], 也就是說你這三週一直在陪C 女朋友的概率最大.

昇華

思考,機器學習的演算法哲學是什麼? 是根據有限的已知去推斷未知. 這又可分為兩種, 一種是根據知識,對未來給出一個確定性判斷,比如decision tree; 還有一是對未來的不確定性懷敬畏,對未知只做概率性預測,如果一定要給出個結果,那隻好用最大化概率法給出. 兩種方法沒有孰優孰劣,只是適用範圍,場景,資料不同而已.

本文分享的HMM 是貝葉斯網路的一個特例. 在推導過程中用到了一些貝葉斯網路相關的知識.貝葉斯網路是用有向無環圖來表示變數間的依賴關係.

貝葉斯網路則屬於更大範疇的概率圖模型(Probabilistic Graphical Model, PGM). 而概率圖模型則是概率模型的一種具體實現.

概率模型就是上面所說的,對未知進行概率性預測. 其核心是對未知進行概率分佈預測,這右可分為兩種: '生成(generative)模型'與'判別(discriminative)模型'.具體地, 可觀測變數集 O, 興趣變數集 Y(即所要求解的變數),其他相關變數 R.

生成式關心的是聯合概率分佈: P(Y, R, O); 而 判別式則關注條件概率 P(Y, R | O).

參考文獻

1. Artificial Intelligence: A modern approach, 3rd edition, 2010, Stuart Russell and Peter Norvig.

2. 統計學方法,2012,李航.(注: 文中例子根據本書中例子改編~)
3. 機器學習, 2016, 周志華.
4. Pattern Recognition and Machine Learning, 2006 ,Christopher M. Bishop.

5. HMM, 2017,Wikipedia.