卷積神經網路 — 特殊應用：人臉識別和神經風格遷移

Part 1：人臉識別

1. 人臉驗證和人臉識別

人臉驗證（Verification）：

• Input：圖片、名字/ID；
• Output：輸入的圖片是否是對應的人。
• 1 to 1 問題。

人臉識別（Recognition）：

• 擁有一個具有K個人的資料庫；
• 輸入一副人臉圖片；
• 如果圖片是任意這K個人中的一位，則輸出對應人的ID。

人臉識別問題對於人臉驗證問題來說，具有更高的難度。如對於一個驗證系統來說，如果我們擁有99%的精確度，那麼這個驗證系統已經具有了很高的精度；但是假設在另外一個識別系統中，如果我們把這個驗證系統應用在具有K個人的識別系統中，那麼系統犯錯誤的機會就變成了K倍。所以如果我們想在識別系統中得到更高的精度，那麼就需要得到一個具有更高精度的驗證系統。

2. one shot learning

對於大多數的人臉識別系統都存在的一個問題就是one shot learning。

什麼是one shot learning：

對於一個人臉識別系統，我們需要僅僅通過先前的一張人臉的圖片或者說一個人臉的樣例，就能夠實現該人的識別，那麼這樣的問題就是one shot 問題。對於存在於資料庫中的人臉圖片，系統能夠識別到對應的人；而不在資料庫中的人臉圖片，則系統給出無法通過識別的結果。

對於one shot learning 問題，因為只有單個樣本，是不足以訓練一個穩健的卷積神經網路來進行不同人的識別過程。而且，在有新的樣本成員加入的時候，往往還需要對網路進行重新訓練。所以我們不能以傳統的方法來實現識別系統。

Similarity 函式：

為了能夠讓人臉識別系統實現一次學習，需要讓神經網路學習 Similarity 函式：

• d(img1, img2)：兩幅圖片之間的差異度
• 輸入：兩幅圖片
• 輸出：兩者之間的差異度
• 如果 $d(img1,img2) \le \tau$，則輸出“same”;
• 如果 $d(img1,img2) > \tau$，則輸出“different”.

對於人臉識別系統，通過將輸入的人臉圖片與資料庫中所擁有的圖片成對輸入Similarity函式，兩兩對比，則可解決one shot problem。如果有新的人加入團隊，則只需將其圖片新增至資料庫即可。

3. Siamese 網路

利用Siamese 網路來實現 Similarity 函式。

構建網路：

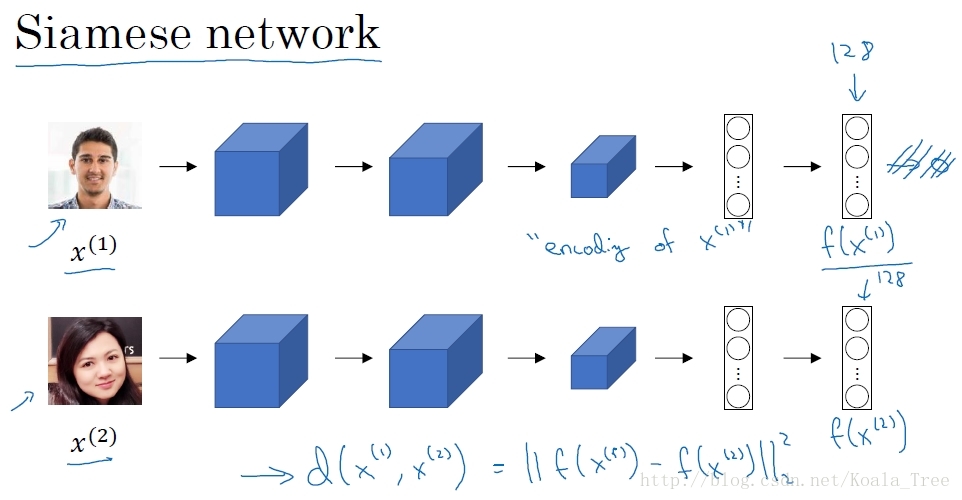
對於一個卷積神經網路結構，我們去掉最後的softmax層，將圖片樣本1輸入網路，最後由網路輸出一個N維的向量（圖中例項以128表示），這N維向量則代表輸入圖片樣本1的編碼。將不同人的圖片樣本輸入相同引數的網路結構，得到各自相應的圖片編碼。

Similarity 函式實現：

將Similarity 函式表示成兩幅圖片編碼之差的範數：

$d(x1,x2) = {\parallel f(x1) - f(x2)\parallel}_2^2$

那麼也就是說：

• 我們的神經網路的引數定義了圖片的編碼；

• 學習網路的引數，使我們得到好的Similarity 函式：

  • 如果x1，x2是同一個人的圖片，那麼得到的${\parallel f(x1) - f(x2)\parallel}_2^2$很小；

  • 如果x1，x2不是同一個人的圖片，那麼得到的${\parallel f(x1) - f(x2)\parallel}_2^2$很大。

4. Triplet 損失

如何通過學習神經網路的引數，得到優質的人臉圖片的編碼？方法之一就是定義 Triplet 損失函式，並在其之上運用梯度下降。

學習目標：

為了使用Triplet 損失函式，我們需要比較成對的影象（三元組術語）：

• Anchor （A）： 目標圖片；
• Positive（P）：與Anchor 屬於同一個人的圖片；
• Negative（N）：與Anchor不屬於同一個人的圖片。

對於Anchor 和 Positive，我們希望二者編碼的差異小一些；對於Anchor 和Negative，我們希望他們編碼的差異大一些。所以我們的目標以編碼差的範數來表示為：

$d(A,P) = {\parallel f(A) - f(P)\parallel}^2 \le {\parallel f(A) - f(N)\parallel}^2 = d(A,N)$

也就是：

${\parallel f(A) - f(P)\parallel}^2 - {\parallel f(A) - f(N)\parallel}^2 \le 0$

上面的公式存在一個問題就是，當$f(A )= f(P) = f(N) = 0$時，也就是神經網路學習到的函式總是輸出0時，或者$f(A )= f(P) = f(N) = 0$時，也滿足上面的公式，但卻不是我們想要的目標結果。所以為了防止出現這種情況，我們對上式進行修改，使得兩者差要小於一個較小的負數：

${\parallel f(A) - f(P)\parallel}^2 - {\parallel f(A) - f(N)\parallel}^2 \le -\alpha$

一般將$-\alpha$寫成$+\alpha$，稱為“margin”。即：

${\parallel f(A) - f(P)\parallel}^2 - {\parallel f(A) - f(N)\parallel}^2 + \alpha \le 0$

不同 margin值的設定對模型學習具有不同的效果，margin 的作用就是拉大了 Anchor與Positive 圖片對和 Anchor與Negative 圖片對之間的差距。

Triplet 損失函式：

Triplet 損失函式的定義基於三張圖片：Anchor、Positive、Negative。

$L(A,P,N) = max({\parallel f(A) - f(P)\parallel}^2 - {\parallel f(A) - f(N)\parallel}^2 + \alpha, 0)$

整個網路的代價函式：

$J = \sum_{i=1}^{m}L(A^{(i)},P^{(i)},N^{(i)})$

注：這裡triplet損失函式：當前者<=0時，則L(A, P, N) = 0，即損失函式為0；當前者>0時，則L(A, P, N) = 前者，此時，利用梯度下降降低損失函式，正好達到訓練引數的目的，最終訓練好的引數只訓練到d(A, N) - d(A, P) >= alpha，即滿足margin要求。

假設我們有一個10000張片的訓練集，裡面是1000個不同的人的照片樣本。我們需要做的就是從這10000張訓練集中抽取圖片生成（A,P,N）的三元組，來訓練我們的學習演算法，並在Triplet 損失函式上進行梯度下降。

注意：為了訓練我們的網路，我們必須擁有Anchor和Positive對，所以這裡我們必須有每個人的多張照片，而不能僅僅是一張照片，否則無法訓練網路。

三元組（A,P,N）的選擇：

在訓練的過程中，如果我們隨機地選擇圖片構成三元組（A,P,N），那麼對於下面的條件是很容易滿足的：

$d(A,P) + \alpha \le d(A,N)$

所以，為了更好地訓練網路，我們需要選擇那些訓練有“難度”的三元組，也就是選擇的三元組滿足：

$d(A,P) \approx d(A,N)$

• 演算法將會努力使得$d(A,N)$變大，或者使得$d(A,P)$變小，從而使兩者之間至少有一個$\alpha$的間隔；

• 增加學習演算法的計算效率，避免那些太簡單的三元組。

注：這裡提到選擇 d(A, P) 約等於 d(A, N)，好處之一是提升學習演算法的計算效率，原因正是在於當隨機選擇的時候d(A, N)普遍偏大，此時，很容易滿足$d(A, P) + \alpha &lt;= d(A，N)$，這時候網路並不會進行訓練，只有當不滿足此條件時候才會進行梯度下降進行引數訓練，故而這裡找不容易滿足的放進去訓練模型正好起到提升計算效率的功能。

最終通過訓練，我們學習到的引數，會使得對於同一個人的圖片，編碼的距離很小；對不同人的圖片，編碼的距離就很大。

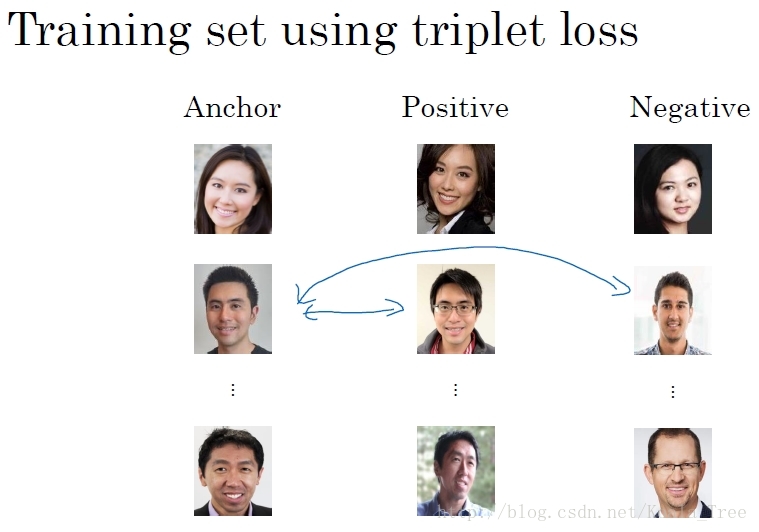
對於大型的人臉識別系統，常常具有上百萬甚至上億的訓練資料集，我們並我容易得到。所以對於該領域，我們常常是下載別人在網上上傳的預訓練模型，而不是從頭開始。

5. 臉部驗證和二分類

除了利用 Triplet 損失函式來學習人臉識別卷積網路引數的方法外，還有其他的方式。我們可以將人臉識別問題利用Siamese網路當成一個二分類問題，同樣可以實現引數的學習。

Siamese 二分類改進：

對兩張圖片應用Siamese 網路，計算得到兩張圖片的N維編碼，然後將兩個編碼輸入到一個logistic regression 單元中，然後進行預測。如果是相同的人，那麼輸出是1；如果是不同的人，輸出是0。那麼這裡我們就將人臉識別的問題，轉化為一個二分類問題。

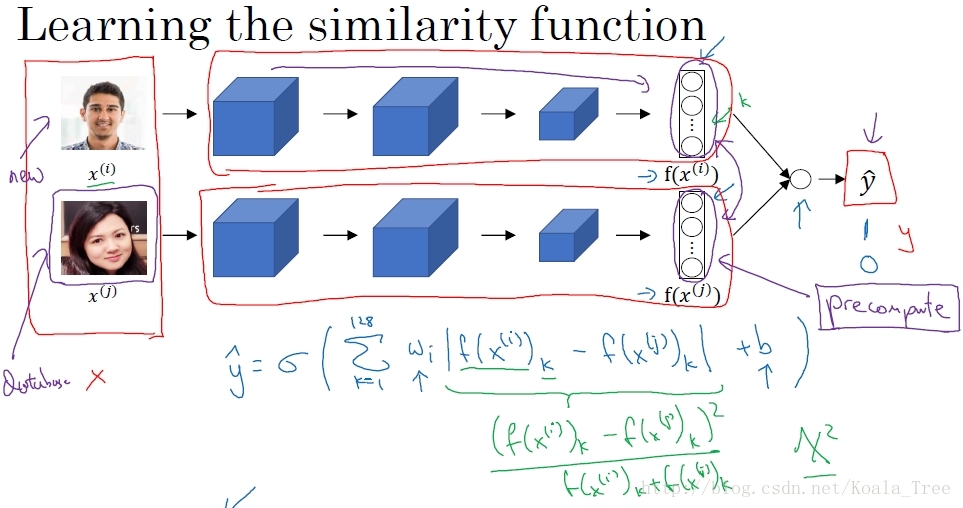
對於最後的sigmoid函式，我們可以進行如下計算：

$\hat{y} = \sigma(\sum_{k=1}^{N}w_i \mid f(x^{(i)})_k - f(x^{(j)})_k \mid + b)$

其中，$f(x^{(i)})$代表圖片$x^{(i)}$的編碼，下標k代表選擇N維編碼向量中的第k個元素。

我們以兩個圖片編碼向量對應元素之間的差值作為特徵輸入到logistic regression 的單元中，增加引數 $w_i$ 和 b，通過訓練得到合適的引數權重和偏置，進而判斷兩張圖片是否為同一個人。

同時輸入邏輯迴歸單元的特徵可以進行更改，如還可以是：

$\frac{(f(x^{(i)})_k - f(x^{(j)})_k)^2}{f(x^{(i)})_k - f(x^{(j)})_k}$

上式也被稱為$chi$方公式，有時也稱為$chi$方相似度。

在實際的人臉驗證系統中，我們可以對資料庫的人臉圖片進行預計算，儲存卷積網路得到的編碼。當有圖片進行識別時，運用卷積網路計算新圖片的編碼，與預計算儲存好的編碼輸入到邏輯迴歸單元中進行預測。這樣可以提高我們系統預測的效率，節省計算時間。

注：該trick也同樣可以用到上面triplet loss function中，即提前將圖片進行預編碼（走一遍Siamese網路，得到去掉softmax層的輸出神經元的值），就避免了後續再對資料庫image進行計算編碼，提升了效率，如果不儲存圖片，同時還能節省空間（對於大型資料集）。

總結：

利用Siamese 網路，我們可以將人臉驗證當作一個監督學習，建立成對的訓練集和是否同一個人的輸出標籤。

我們利用不同的圖片對，使用反向傳播的演算法對Siamese網路進行訓練，進而得到人臉驗證系統。

注：不管是利用Siamese網路進行編碼+triplet損失函式，還是採用Siamese網路編碼+logistic regression二分類，其最重要的是學到一個有效的Siamese網路，即對同一個人照片之間的編碼近似（距離較近），不同人之間的編碼差異較大（距離較遠）。

Part 2：神經風格遷移

6. 深度網路學習內容視覺化

如何視覺化：

假設我們訓練了一個卷積神經網路如下所示：

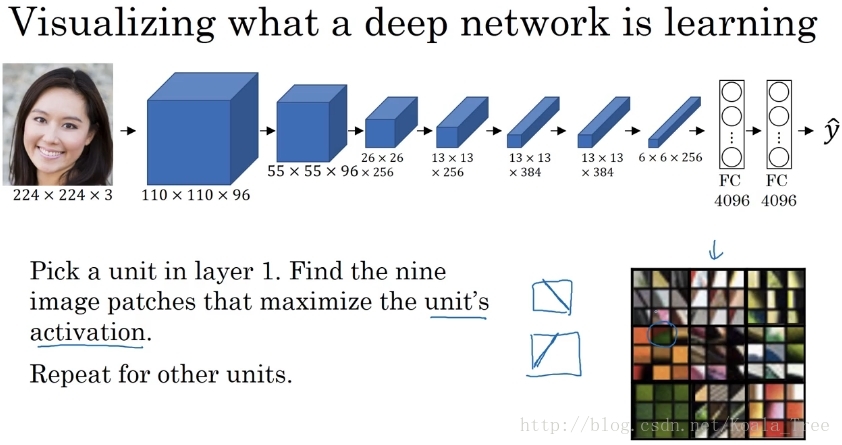
我們希望看到不同層的隱藏單元的計算結果。依次對各個層進行如下操作：

• 在當前層挑選一個隱藏單元；
• 遍歷訓練集，找到最大化地激活了該運算單元的圖片或者圖片塊；
• 對該層的其他運算單元執行操作。

對於在第一層的隱藏單元中，其只能看到卷積網路的小部分內容，也就是最後我們找到的那些最大化啟用第一層隱層單元的是一些小的圖片塊。我們可以理解為第一層的神經單元通常會尋找一些簡單的特徵，如邊緣或者顏色陰影等。

各層網路視覺化：

對於卷積網路的各層單元，隨著網路深度的增加，隱藏層計算單元隨著層數的增加，從簡單的事物逐漸到更加複雜的事物。

7. 神經風格遷移代價函式

代價函式：

為了實現神經風格遷移，我們需要為生成的圖片定義一個代價函式。

對於神經風格遷移，我們的目標是由內容圖片C和風格圖片S，生成最終的風格遷移圖片G：

所以為了實現神經風格遷移，我們需要定義關於G的代價函式J，以用來評判生成圖片的好壞：

$J(G) = \alpha J_{content}(C,G) + \beta J_{style}(S,G)$

其中

• $J_{content}(C,G)$代表生成圖片G的內容和內容圖片C的內容的相似度；

• $J_{style}(S,G)$