以下為在Coursera上吳恩達老師的 DeepLearning.ai 課程專案中，第四部分《卷積神經網路》第二週課程“深度卷積模型”關鍵點的筆記。本次筆記幾乎涵蓋了所有視訊課程的內容。在閱讀以下筆記的同時，強烈建議學習吳恩達老師的視訊課程，視訊請至 Coursera 或者 網易雲課堂。

同時我在知乎上開設了關於機器學習深度學習的專欄收錄下面的筆記，以方便大家在移動端的學習。歡迎關注我的知乎：大樹先生。一起學習一起進步呀！^_^

卷積神經網路 — 深度卷積模型

1. 經典的卷積網路

介紹幾種經典的卷積神經網路結構，分別是LeNet、AlexNet、VGGNet。

LeNet-5：

LeNet-5主要是針對灰度設計的，所以其輸入較小，為32×32×1，其結構如下：

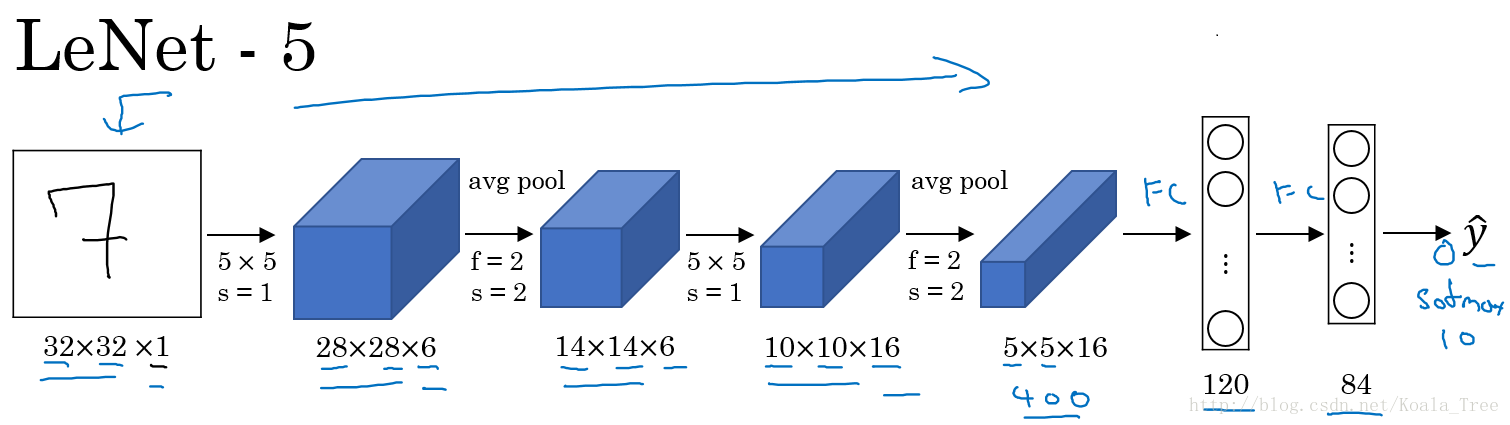
在LetNet中，存在的經典模式：

• 隨著網路的深度增加，影象的大小在縮小，與此同時，通道的數量卻在增加；
• 每個卷積層後面接一個池化層。

AlexNet：

AlexNet直接對彩色的大圖片進行處理，其結構如下：

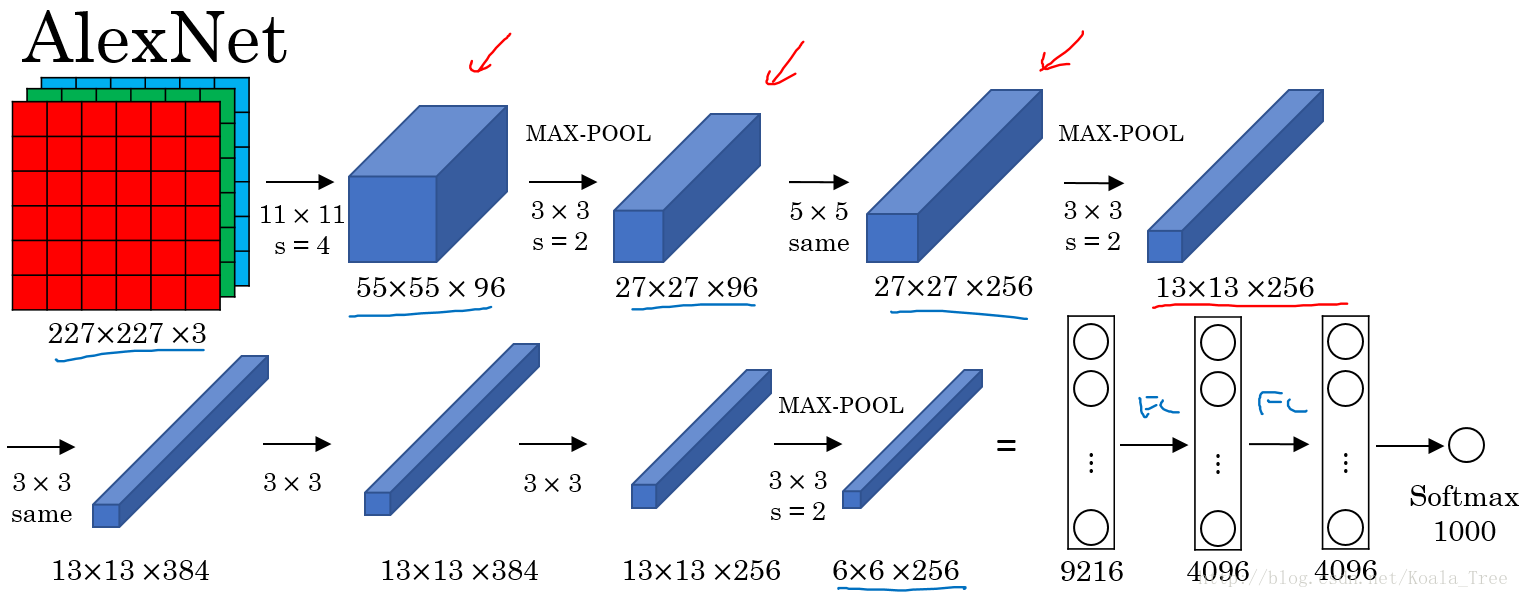
• 與LeNet相似，但網路結構更大，引數更多，表現更加出色；
• 使用了Relu；
• 使用了多個GPUs；
• LRN（後來發現用處不大，丟棄了）

AlexNet使得深度學習在計算機視覺方面受到極大的重視。

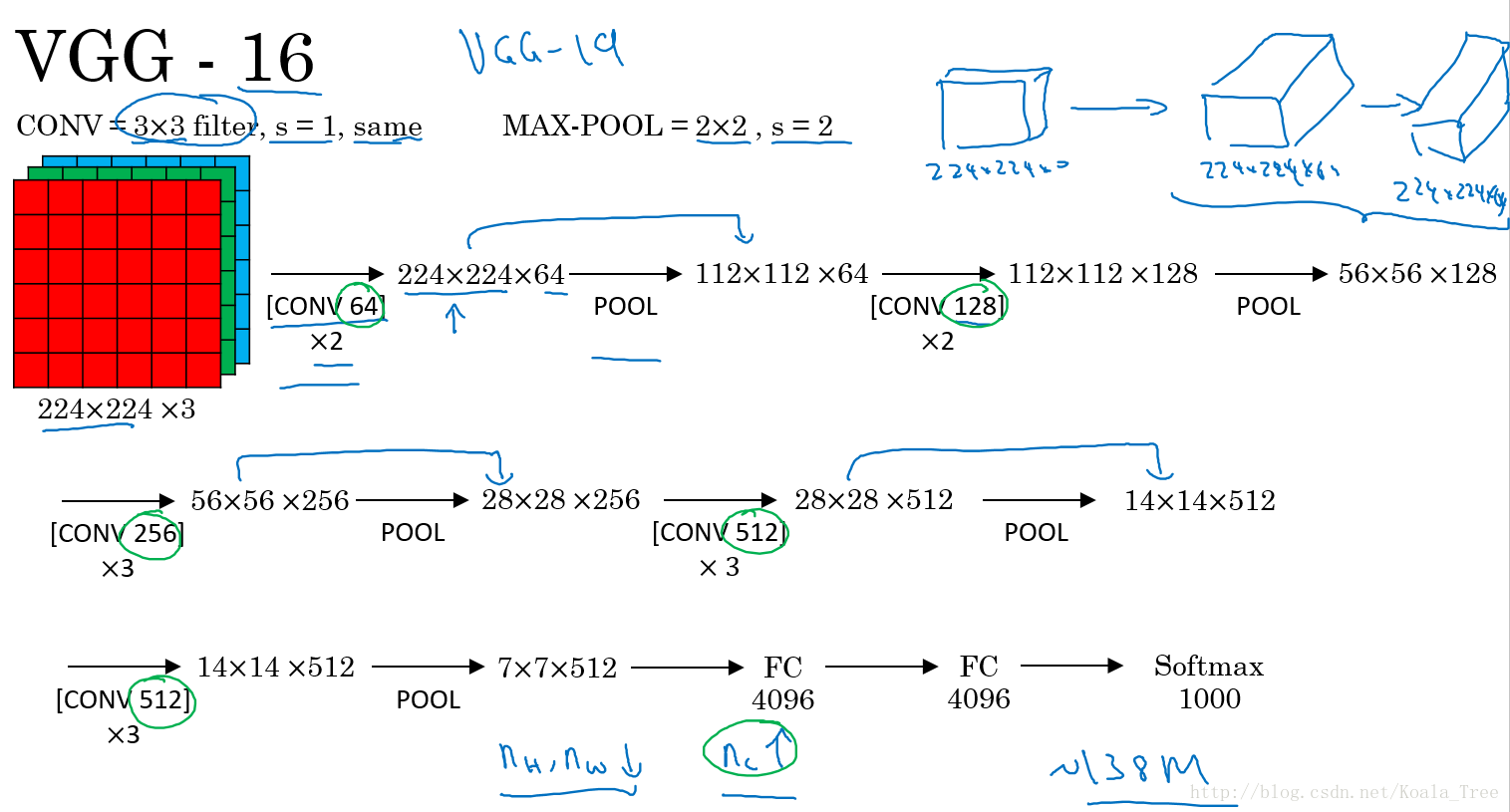
VGG-16：

VGG卷積層和池化層均具有相同的卷積核大小，都使用3×3，

stride=1,SAME的卷積和2×2，stride=2 的池化。其結構如下：

2. ResNet

ResNet是由殘差塊所構建。

殘差塊：

下面是一個普通的神經網路塊的傳輸：

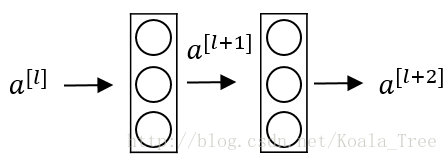
其前向傳播的計算步驟為：

• Linear：z[l+1]=W[l+1]a[l]+b[l+1]
• Relu：a[l+1]=g(z[l+1])
• Linear：z[l+2]=W[l+2]a[l+1]+b[l+2]
• Relu：a[l+2]=g(z[l+2])

而ResNet塊則將其傳播過程增加了一個從a[l]直接到z[l+2]的連線，將其稱之為“short cut”或者“skip connection”：

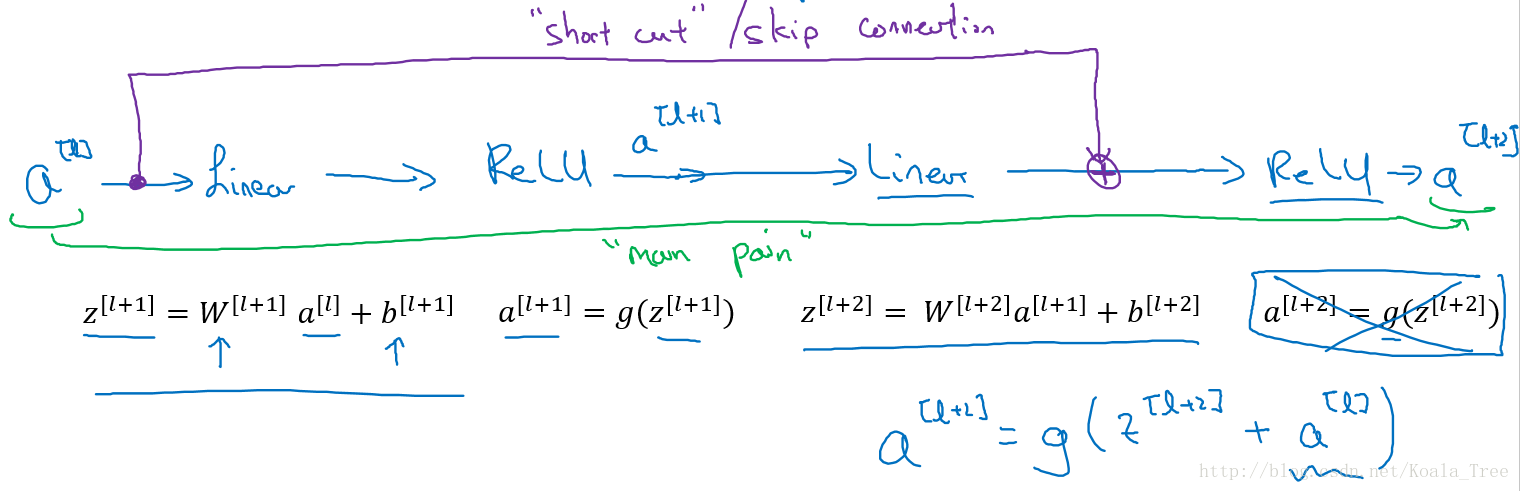
也就是前向傳播公式的最後一個步驟變為：a[l+2]=g(z[l+2]+a[l])

增加“short cut”後，成為殘差塊的網路結構：

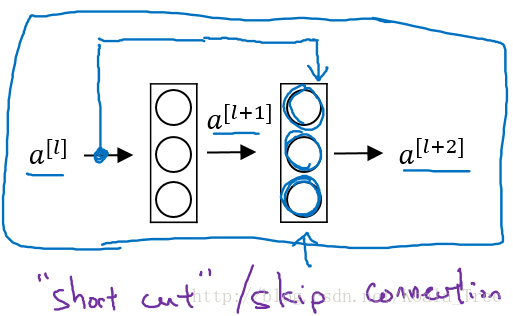
注意這裡是連線在Relu啟用函式之前。

Residual Network：

多個殘差塊堆積起來構成ResNet網路結構，其結構如下：

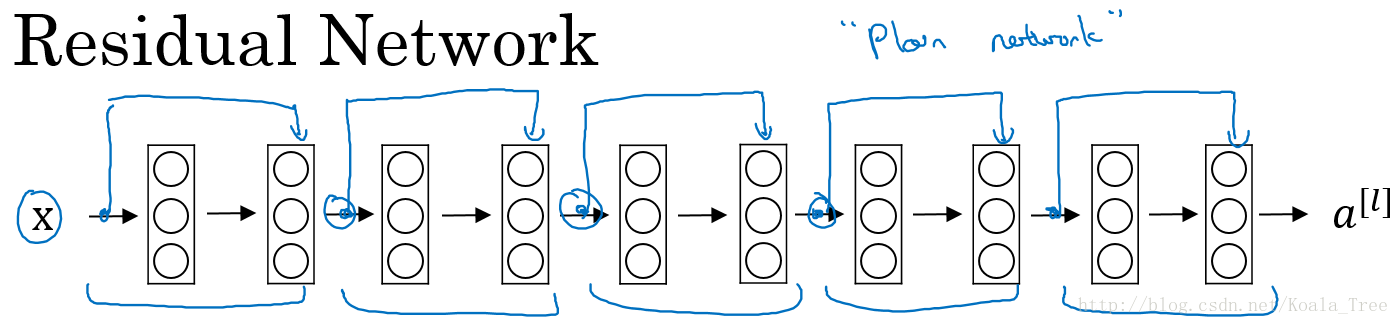
沒有“short cut”的普通神經網路和ResNet的誤差曲線：

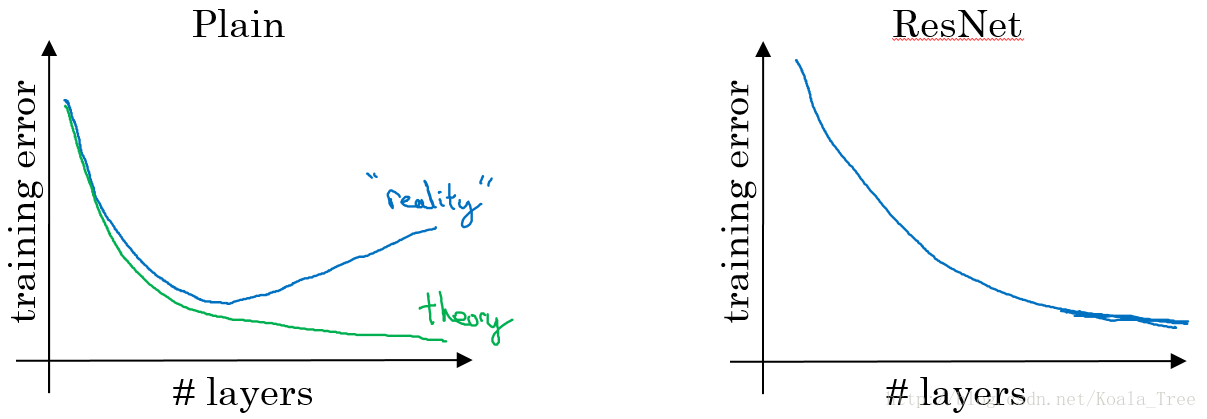
• 在沒有殘差的普通神經網路中，訓練的誤差實際上是隨著網路層數的加深，先減小再增加；
• 在有殘差的ResNet中，即使網路再深，訓練誤差都會隨著網路層數的加深逐漸減小。

ResNet對於中間的啟用函式來說，有助於能夠達到更深的網路，解決梯度消失和梯度爆炸的問題。

3. ResNet表現好的原因

假設有個比較大的神經網路，輸入為x，輸出為a[l]。如果我們想增加網路的深度，這裡再給網路增加一個殘差塊：

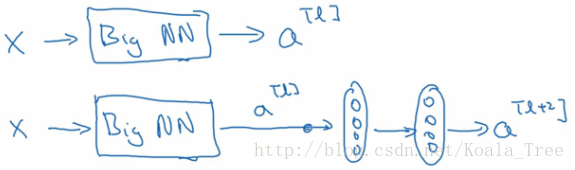
假設網路中均使用Relu啟用函式，所以最後的輸出a⩾0。這裡我們給出a[l+2]的值：

a[l+2]=g(z[l+2]+a[l])=g(W[l+2]a[l+1]+b[l+2]+a[l])

如果使用L2正則化或者權重衰減，會壓縮W和b的值，如果W[l+2]=0同時b[l+2]=0，那麼上式就變成：

a[l+2]=g(z[l+2]+a[l])=g(a[l])=relu(a[l])=a[l]

所以從上面的結果我們可以看出，對於殘差塊來學習上面這個恆等函式是很容易的。所以在增加了殘差塊後更深的網路的效能也並不遜色於沒有增加殘差塊簡單的網路。所以儘管增加了網路的深度，但是並不會影響網路的效能。同時如果增加的網路結構能夠學習到一些有用的資訊，那麼就會提升網路的效能。

同時由於結構a[l+2]=g(z[l+2]+a[l])，ResNet在設計中使用了很多相同的卷積，以保持z[l+2]和a[l]的維度相同。

將普通深度神經網路變為ResNet：

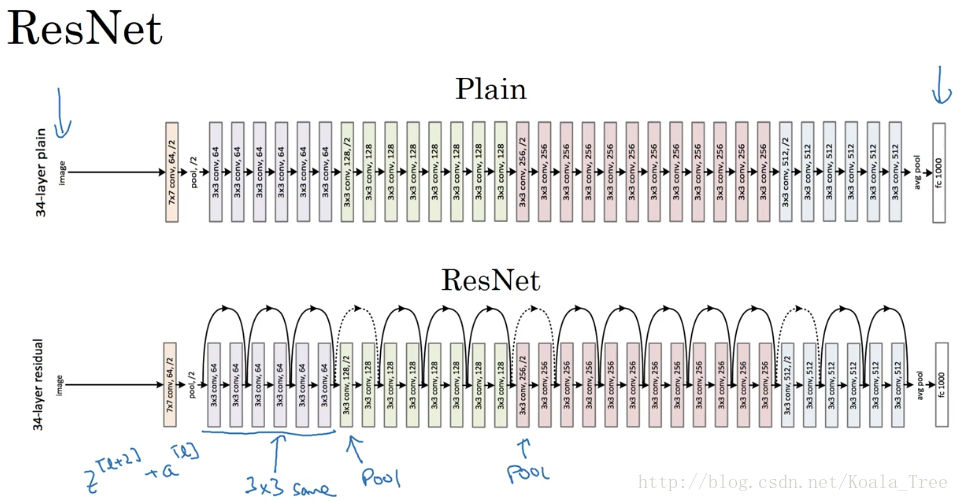
在兩個相同的卷積層之間增加“skip connection”。

4. 1x1卷積

1x1卷積：

在二維上的卷積相當於圖片的每個元素和一個卷積核數字相乘。

但是在三維上，與1×1