機器學習常用演算法（LDA,CNN,LR）原理簡述
1.LDA
LDA是一種三層貝葉斯模型，三層分別為：文件層、主題層和詞層。該模型基於如下假設：
1）整個文件集合中存在k個互相獨立的主題；
2）每一個主題是詞上的多項分佈；
3）每一個文件由k個主題隨機混合組成；
4）每一個文件是k個主題上的多項分佈；
5）每一個文件的主題概率分佈的先驗分佈是Dirichlet分佈；
6）每一個主題中詞的概率分佈的先驗分佈是Dirichlet分佈。
文件的生成過程如下：
1）對於文件集合M，從引數為β的Dirichlet分佈中取樣topic生成word的分佈引數φ；
2）對於每個M中的文件m，從引數為α的Dirichlet分佈中取樣doc對topic的分佈引數θ；
3）對於文件m中的第n個詞語W_mn，先按照θ分佈取樣文件m的一個隱含的主題Z_m，再按照φ分佈取樣主題Z_m的一個詞語W_mn。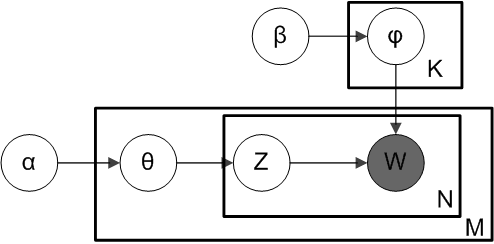
因此整個模型的聯合分佈，如下：
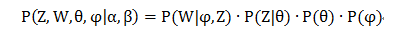
對聯合分佈求積分，去掉部分隱變數後：
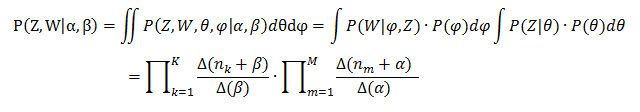
用間接計算轉移概率可以消除中間引數θ和φ，所以主題的轉移概率化為：
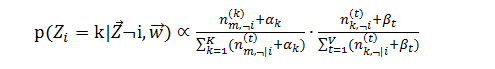
這樣我們就可以通過吉布斯取樣來進行每輪的迭代，迭代過程即：首先產生於一個均勻分佈的隨機數，然後根據上式計算每個轉移主題的概率，通過累積概率判斷隨機數落在哪個new topic下，更新引數矩陣，如此迭代直至收斂。
2.CNN
2.1 多層感知器基礎
單個感知器的結構示例如下：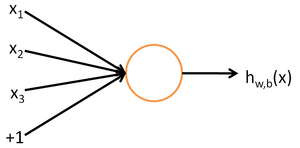
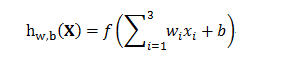
其中函式f為啟用函式，一般用sigmoid函式。
將多個單元組合起來並具有分層結構時，就形成了多層感知器模型(神經網路)。下圖是一個具有一個隱含層(3個節點)和一個單節點輸出層的神經網路。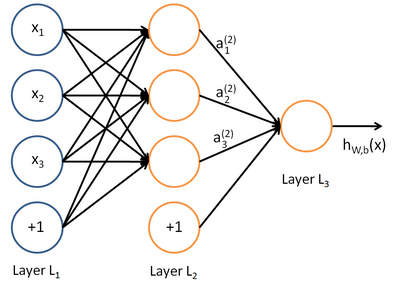
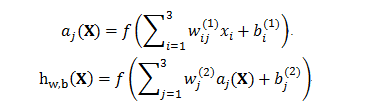
2.2 卷積神經網路
2.2.1 結構特徵
在影象處理中，往往把影象表示為畫素的向量，比如一個1000×1000的影象，可以表示為一個〖10〗^6的向量。在上述的神經網路中，如果隱含層數目與輸入層一樣，即也是〖10〗^6時，那麼輸入層到隱含層的引數資料為〖10〗^12，這樣就太多了，基本沒法訓練。因此需要減少網路的引數。
卷積網路就是為識別二維形狀而特殊設計的一個多層感知器，這種網路結構對平移、比例縮放、傾斜或者共他形式的變形具有高度不變性。這些良好的效能是網路在有監督方式下學會的，網路的結構主要有稀疏連線和權值共享兩個特點，包括如下形式的約束：
1）特徵提取。每一個神經元從上一層的區域性接受域得到輸入，因而迫使它提取區域性特徵。一旦一個特徵被提取出來，只要它相對於其他特徵的位置被近似地保留下來，它的精確位置就變得沒有那麼重要了。
2）特徵對映。網路的每一個計算層都是由多個特徵對映組成的，每個特徵對映都是平面形式的，平面中單獨的神經元在約束下共享相同的權值集。
3）子抽樣。每個卷積層後面跟著一個實現區域性平均和子抽樣的計算層，由此特徵對映的解析度降低。這種操作具有使特徵對映的輸出對平移和其他形式的變形的敏感度下降的作用。
在一個卷積網路的所有層中的所有權值都是通過有監督訓練來學習的，此外，網路還能自動的在學習過程中提取特徵。
一個卷積神經網路一般是由卷積層和子抽樣層交替組成。下圖是一個例子：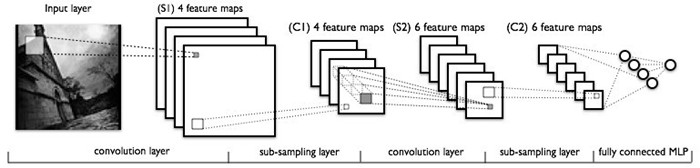
輸入的圖片經過卷積層，子抽樣層，卷積層，子抽樣層之後，再由一個全連線成得到輸出。
2.2.2 卷積層
卷積層是通過權值共享實現的。共享權值的單元構成一個特徵對映，如下圖所示。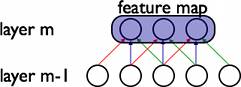
在圖中，有3個隱層節點，他們屬於同一個特徵對映。同種顏色的連結的權值是相同的，這裡仍然可以使用梯度下降的方法來學習這些權值，只需要對原始演算法做一些小的改動，共享權值的梯度是所有共享引數的梯度的總和。
2.2.3 子抽樣層
子抽樣層通過區域性感知實現。一般認為人對外界的認知是從區域性到全域性的，而影象的空間聯絡也是區域性的畫素聯絡較為緊密，而距離較遠的畫素相關性則較弱。因而，每個神經元其實沒有必要對全域性影象進行感知，只需要對區域性進行感知，然後在更高層將區域性的資訊綜合起來就得到了全域性的資訊。如下圖所示：左圖為全連線，右圖為區域性連線。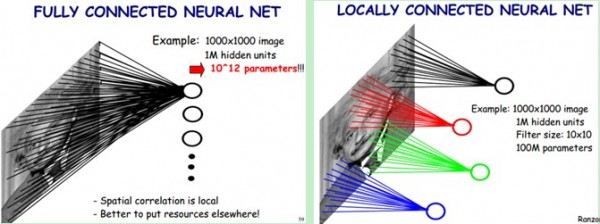
3.LR
線性迴歸模型，一般表達為h_θ (x)= θ^T X 形式，輸出域是整個實數域，可以用來進行二分類任務，但實際應用中對二分類問題人們一般都希望獲的一個[0,1]範圍的概率值，比如生病的概率是0.9或者0.1，sigmoid函式g(z)可以滿足這一需求，將線性迴歸的輸出轉換到[0,1]。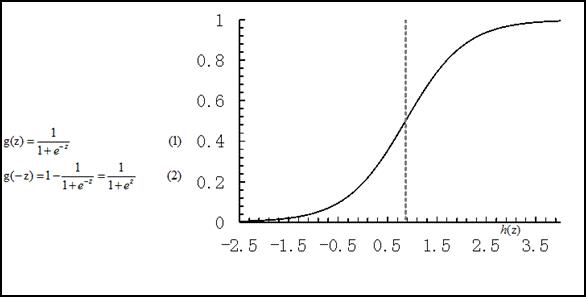
利用g(z)，可以獲取樣本x屬於類別1和類別0的概率p(y = 1 |x,θ)，p(y = 0|x,θ)，變成邏輯迴歸的形式：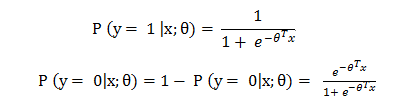
取分類閾值為0.5，相應的決策函式為：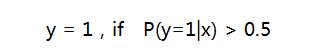
取不同的分類閾值可以得到不同的分類結果，如果對正例的判別準確性要求高，可以選擇閾值大一些，比如 0.6，對正例的召回要求高，則可以選擇閾值小一些，比如0.3。
轉換後的分類面（decision boundary）與原來的線性迴歸是等價的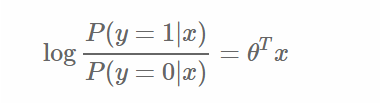
3.1 引數求解
模型的數學形式確定後，剩下就是如何去求解模型中的引數。統計學中常用的一種方法是最大似然估計，即找到一組引數，使得在這組引數下，我們的資料的似然值（概率）越大。在邏輯迴歸模型中，似然值可表示為：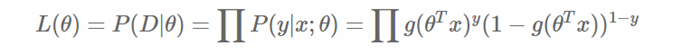
取對數可以得到對數似然值：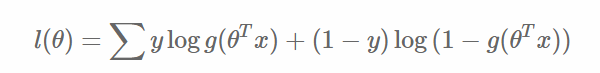
另一方面，在機器學習領域，我們更經常遇到的是損失函式的概念，其衡量的是模型預測的誤差，值越小說明模型預測越好。常用的損失函式有0-1損失，log損失，hinge損失等。其中log損失在單個樣本點的定義為：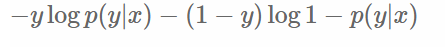
定義整個資料集上的平均log損失，我們可以得到：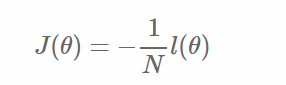
即在邏輯迴歸模型中，最大化似然函式和最小化log損失函式實際上是等價的。對於該優化問題，存在多種求解方法，這裡以梯度下降的為例說明。梯度下降(Gradient Descent)又叫最速梯度下降，是一種迭代求解的方法，通過在每一步選取使目標函式變化最快的一個方向調整引數的值來逼近最優值。基本步驟如下：
選擇下降方向（梯度方向，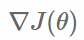
）
選擇步長，更新引數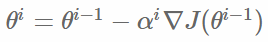
重複以上兩步直到滿足終止條件。
3.2 分類邊界
知道如何求解引數後，我們來看一下模型得到的最後結果是什麼樣的。很容易可以從sigmoid函式看出，取0.5作為分類閾值，當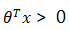 
時，y=1，否則 y=0。
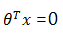是模型隱含的分類平面（在高維空間中，一般叫做超平面）。所以說邏輯迴歸本質上是一個線性模型，但這不意味著只有線性可分的資料能通過LR求解，實際上，可以通過特徵變換的方式把低維空間轉換到高維空間，而在低維空間不可分的資料，到高維空間中線性可分的機率會高一些。下面兩個圖的對比說明了線性分類曲線和非線性分類曲線（通過特徵對映）。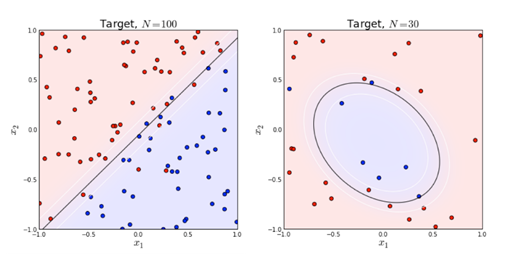
左圖是一個線性可分的資料集，右圖在原始空間中線性不可分，但是在特徵轉換 [x1,x2]=>[x1,x2,x21,x22,x1x2] 後的空間是線性可分的，對應的原始空間中分類邊界為一條類橢圓曲線
3.3 Word2Vec
Word2Vec有兩種網路模型，分別為CBOW模型（Continuous Bag-of-Words Model）和Sikp-gram模型（Continuous Skip-gram Model）。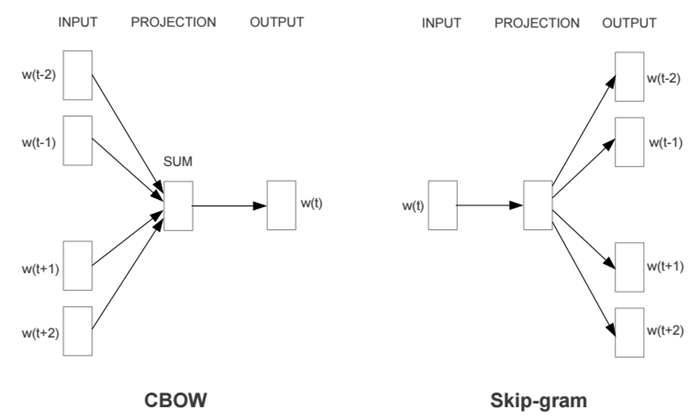
兩個模型都包含三層：輸入層、投影層和輸出層。其中，CBOW模型是在已知當前詞w(t)的上下文w(t-2)、w(t-1)、w(t+1)、w(t+2)的情況下來預測詞w(t)，Skip-gram模型則恰恰相反，它是在已知當前詞w(t)的情況下來預測當前詞的上下文w(t-2)、w(t-1)、w(t+1)、w(t+2)。例如，“今天/天氣/好/晴朗”，而當前詞為“天氣”。CBOW模型是預測“今天”、“好”、“晴朗”之間出現“天氣”的概率，而Skip-gram模型是預測“天氣”的周圍出現“今天”、“好”、“晴朗”三個詞的概率。
CBOW模型通過優化如下的目標函式來求解，目標函式為一個對數似然函式。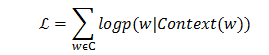
CBOW的輸入為包含Context(w)中2c個詞的詞向量v(w)，這2c個詞向量在投影層累加得到輸出層的輸出記為X_w。輸出層採用了Hierarchical Softmax的技術，組織成一棵根據訓練樣本集的所有詞的詞頻構建的Huffman樹，實際的詞為Huffman樹的葉子節點。通過長度為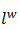 
的路徑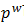 
可以找到詞w，路徑可以表示成由0和1組成的串，記為
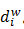。Huffman數的每個中間節點都類似於一個邏輯迴歸的判別式，每個中間節點的引數記為 
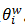。那麼，對於CBOW模型來說，有：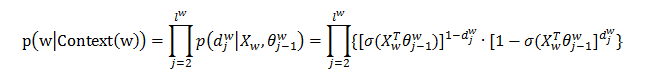
那麼，目標函式為：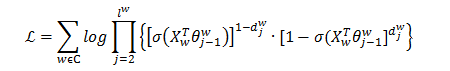
那麼通過隨機梯度下降法更新目標函式的引數θ和X，使得目標函式的值最大即可。
與CBOW模型類似，Skip-gram通過優化如下的目標函式來求解。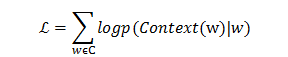
其中：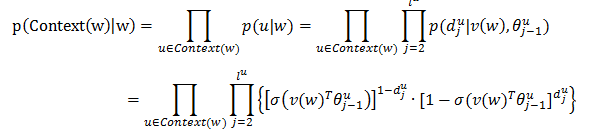
那麼，Skip-gram的目標函式為：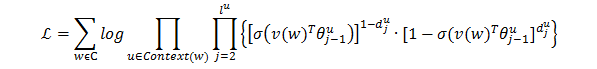
通過隨機梯度下降法更新目標函式的引數θ和v(w)，使得目標函式的值最大即可。