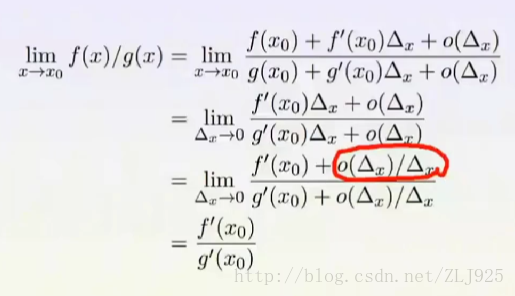前言，建議大家如果有打算把數學這塊兒搞明白，最好把考研的時候用的數三的三大本書（高等數學，概率論與數理統計、線性代數三本書）買過來，再研究下各個結論是如何證明的，學過的東西再拾起來很容易的。
本文主要內容：

極限
複習極限記號，無窮大無窮小階數
微分學
複習函式求導，泰勒級數逼近
牛頓法與梯度下降法
Jensen不等式
複習凸函式，Jensen不等式重點內容的證明

常用的數學記號：

極限：

極限：如何比較無窮小？

極限：無窮小階數
如果f(x) 為n階以上無窮小，那麼說明f(x)趨於0的速度比分母還快。

弧長公式:弧長=θ*r,θ是弧度r是半徑

微分學

微分學——多元函式：

以上兩圖等式左邊的x和y，應分別改為Xo、Yo

例子1：

例子2：

一元微分學的頂峰：泰勒級數
用多項式逼近的方式描述高階導數，我們就得到了泰勒級數。
泰勒／麥克勞林級數：多項式逼近

洛必達法則是在一定條件下通過分子分母分別求導再求極限來確定未定式值的方法。這種方法主要是在一定條件下通過分子分母分別求導再求極限來確定未定式的值．
在運用洛必達法則之前，首先要完成兩項任務：
一是分子分母的極限是否都等於零(或者無窮大)；
二是分子分母在限定的區域內是否分別可導；

如果這兩個條件都滿足，接著求導並判斷求導之後的極限是否存在：
如果存在，直接得到答案；
如果不存在，則說明此種未定式不可用洛必達法則來解決；

如果不確定，即結果仍然為未定式，再在驗證的基礎上繼續使用洛必達法則

牛頓法與梯度下降法：
牛頓法與梯度下降法本質也是逼近。

y=ax2+bx+c(a 不等於 0)
（1）函式開口向上,即a>0時,則沒有最大值,只有最小值,即函式的頂點,可用函式的頂點公式：(-b/2a,(4ac-b^2)/4a)來求.
（2）函式開口向上,即a<0時,則沒有最小值,只有最大值,求法同上.

牛頓法與梯度下降法：

例子：

小結：

凸函式與琴生不等式：
為什麼研究凸函式，凸優化？
對於凸優化來說，區域性極值與整體極值沒有區別。這個比較簡單，所以從這個開始研究。
當不知道該做什麼的時候，選擇最簡單的問題開始做起。這也是數學家慣用的伎倆。

凸函式定義：

凸函式判斷準則：

凸函式重要性質：琴生不等式（凸函式定義的推廣）

證明過程：從中間的不等式開始看。