【詳解】樹狀陣列
引入
如果給你n個數,然後進行q次詢問,每次詢問一個區間[x,y]的和,你會怎麼做?
第一種方法:最簡單的方法,用陣列存起來,每次列舉x-y,ans加起來就可以,時間複雜度O(qn),十分慢。
第二種方法:或許大多數人會使用字首和陣列:sum[i]=a[1]+a[2]+…+a[i],所以求[x,y]只需要輸出sum[y]-sum[x-1]即可,時間複雜度O(n),這是最快的方法之一了。
但是,如果加上一個條件:在q次詢問中,有可能會臨時使a[m]加上或減去一個數k(我們令這個為update(m,k)操作),也有可能會查詢一個區間的和,怎麼辦呢?
如果還是用字首和陣列,就不方便了,因為update(m,k)需要更新sum[m]到sum[n]的值,於是時間複雜度又變為了O(qn)。
那麼怎麼辦呢?於是有了樹狀陣列。
樹狀陣列
概念
樹狀陣列,時間複雜度log級別的資料結構,且實現複雜度極小,不論是上面提到的update操作還是求字首和。
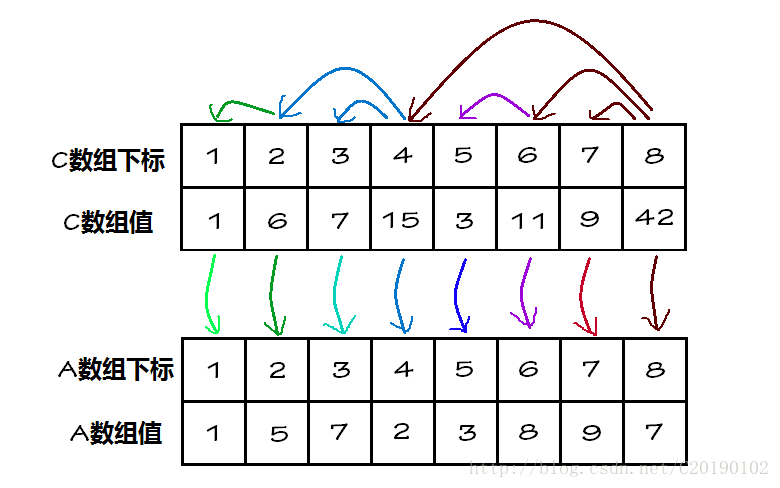
如圖,A陣列是原始n個數的陣列,C陣列就是是樹狀陣列(“樹狀”陣列,是指一個普通陣列,按樹狀儲存,而不是一種STL中的資料結構)。
實現
觀察一下有什麼規律。
- C[1] = A[1]
- C[2] = C[1] + A[2] = A[1] + A[2]
- C[3] = A[3]
- C[4] = C[2] + C[3] +A[4] = A[1] + A[2] + A[3] + A[4]
- C[5] = A[5]
- C[6] = C[5] + A[6] = A[5] + A[6]
- C[7] = A[7]
- C[8] = C[4] + C[6] + C[7] + A[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]
不難發現,好像和二進位制很有關係。
但是很難再想下去,事實上是這樣的:
定義lowbit(x)為x二進位制下末尾0的個數。
則含有C[i0]的C陣列中的位置有:
i0
i1 = i0 + lowbit(i0)
i2 = i1 + lowbit(i1)
i3 =
… …
ik = ik−1 + lowbit(ik−1)
(ik≤n)
如果沒法理解,寫一個迴圈就懂了:
for(int i=x;i<=n;i+=lowbit(i))- 1
計算lowbit
lowbit(x)=x&-x
為什麼?這裡複製了一篇證明(懶得打)
首先明白一個概念,計算機中-i=(i的取反+1),也就是i的補碼
而lowbit,就是求(樹狀陣列中)一個數二進位制的1的最低位,例如01100110,lowbit=00000010;再例如01100000,lowbit=00100000。
所以若一個數(先考慮四位)的二進位制為abcd,那麼其取反為(1-a)(1-b)(1-c)(1-d),那麼其補碼為(1-a)(1-b)(1-c)(2-d)。
如果d為1,什麼事都沒有-_-|||但我們知道如果d為0,天理不容2Σ( ° △ °|||)︴
於是就要進位。如果c也為0,那麼1-b又要加1,然後又有可能是1-a……直到碰見一個為補碼為0的bit,我們假設這個bit的位置為x
這個時候可以發現:是不是x之前的bit的補碼都與其自身不同?,x之後的補碼與其自身一樣都是0?
例如01101000,反碼為10010111,補碼為10011000,可以看到在原來數正數第五位前,補碼的進位因第五位使其不會受到影響,於是0&1=0,;
但在這個原來數“1”後,所有零的補碼都會因加1而進位,導致在這個“1”後所有數都變成0,再加上0&0=0,所以他們運算結果也都是零;
只有在這個數處,0+1=1,連鎖反應停止,所以這個數就被確定啦O(∩_∩)O
所以and以後只有x這個bit是一……
update操作
當要動態改變一個數時,用剛剛的迴圈枚舉出與它相關的位置,都增加(減少)即可:
void update(int k,int x)
{
for(int i=k;i<=n;i+=lowbit(i))
C[i]+=x;
}- 1
- 2
- 3
- 4
- 5
getsum操作
就是求字首和,同樣的,倒著進行剛剛的迴圈,累加路上的值即可:
int getsum(int x)
{
int ans=0;
for(int i=x;i;i-=lowbit(i))//i要大於0
ans+=C[i];
return ans;
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
關於程式碼風格
樹狀陣列的update和getsum基本是通用的,建議不要自己改函式名,lowbit可以寫函式,也可以巨集定義:#define lowbit(x) (x&-x)