kmeans演算法原理以及實踐操作
kmeans一般在資料分析前期使用，選取適當的k，將資料聚類後，然後研究不同聚類下資料的特點。
演算法原理：
(1) 隨機選取k箇中心點；
(2) 在第j次迭代中，對於每個樣本點，選取最近的中心點，歸為該類；
(3) 更新中心點為每類的均值；
(4) j<-j+1 ,重複(2)(3)迭代更新，直至誤差小到某個值或者到達一定的迭代步數，誤差不變.
空間複雜度o(N)
時間複雜度o(I*K*N)
其中N為樣本點個數，K為中心點個數，I為迭代次數
為什麼迭代後誤差逐漸減小：
SSE= 
對於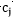
而言，求導後，當
時，SSE最小，對應第(3)步；
對於
而言，求導後，當
時，SSE最小，對應第(2)步。
因此kmeans迭代能使誤差逐漸減少直到不變
輪廓係數：
輪廓係數（Silhouette Coefficient）結合了聚類的凝聚度（Cohesion）和分離度（Separation），用於評估聚類的效果。該值處於-1~1之間，值越大，表示聚類效果越好。具體計算方法如下：
- 對於每個樣本點i，計算點i與其同一個簇內的所有其他元素距離的平均值，記作a(i)，用於量化簇內的凝聚度。
- 選取i外的一個簇b，計算i與b中所有點的平均距離，遍歷所有其他簇，找到最近的這個平均距離,記作b(i)，即為i的鄰居類，用於量化簇之間分離度。
- 對於樣本點i，輪廓係數s(i) = (b(i) – a(i))/max{a(i),b(i)}
- 計算所有i的輪廓係數，求出平均值即為當前聚類的整體輪廓係數，度量資料聚類的緊密程度
從上面的公式，不難發現若s(i)小於0，說明i與其簇內元素的平均距離小於最近的其他簇，表示聚類效果不好。如果a(i)趨於0，或者b(i)足夠大，即a(i)<<b(i)，那麼s(i)趨近與1，說明聚類效果比較好。
K值確定
法1：(輪廓係數)在實際應用中，由於Kmean一般作為資料預處理，或者用於輔助分聚類貼標籤。所以k一般不會設定很大。可以通過列舉，令k從2到一個固定值如10，在每個k值上重複執行數次kmeans(避免區域性最優解)，並計算當前k的平均輪廓係數，最後選取輪廓係數最大的值對應的k作為最終的叢集數目。
法2：(Calinski-Harabasz準則)
其中SSB是類間方差，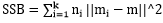
，m為所有點的中心點,mi為某類的中心點；
SSW是類內方差，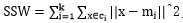
；
(N-k)/(k-1)是複雜度；
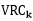比率越大，資料分離度越大.
前提：
Duda-Hart test 看資料集是否適合分為超過1類
初始點選擇方法：
思想，初始的聚類中心之間相互距離儘可能遠.
法1(kmeans++):
1、從輸入的資料點集合中隨機選擇一個點作為第一個聚類中心
2、對於資料集中的每一個點x，計算它與最近聚類中心(指已選擇的聚類中心)的距離D(x)
3、選擇一個新的資料點作為新的聚類中心，選擇的原則是：D(x)較大的點，被選取作為聚類中心的概率較大
4、重複2和3直到k個聚類中心被選出來
5、利用這k個初始的聚類中心來執行標準的k-means演算法
從上面的演算法描述上可以看到，演算法的關鍵是第3步，如何將D(x)反映到點被選擇的概率上，一種演算法如下：
1、先從我們的資料庫隨機挑個隨機點當“種子點”
2、對於每個點，我們都計算其和最近的一個“種子點”的距離D(x)並儲存在一個數組裡，然後把這些距離加起來得到Sum(D(x))。
3、然後，再取一個隨機值，用權重的方式來取計算下一個“種子點”。這個演算法的實現是，先取一個能落在Sum(D(x))中的隨機值Random，然後用Random -= D(x)，直到其<=0，此時的點就是下一個“種子點”。
4、重複2和3直到k個聚類中心被選出來
5、利用這k個初始的聚類中心來執行標準的k-means演算法
法2：選用層次聚類或Canopy演算法進行初始聚類，然後從k個類別中分別隨機選取k個點
，來作為kmeans的初始聚類中心點
優點：
1、 演算法快速、簡單;
2、 容易解釋
3、 聚類效果中上
4、 適用於高維
缺陷：
1、 對離群點敏感，對噪聲點和孤立點很敏感(通過k-centers演算法可以解決)
2、 K-means演算法中聚類個數k的初始化
3、初始聚類中心的選擇，不同的初始點選擇可能導致完全不同的聚類結果。
實踐操作：
R語言
1、####################判斷是否應該分為超過1類##########################
dudahart2(x,clustering,alpha=0.001)
2、###################判斷使用輪廓係數或Calinski-Harabasz準則選用k值，以及是否使用大規模樣本點處理方式##########################################
pamk(data,krange=2:10,criterion="asw", usepam=TRUE,
scaling=FALSE, alpha=0.001, diss=inherits(data, "dist"), critout=FALSE, ns=10, seed=NULL, ...)
3、############利用pamk求出來的k,用kmeans聚類####################
pamk.result <- pamk(data)
pamk.result$nc
kc <- kmeans(data, pamk.result$nc)
4、############畫出k與輪廓係數關係，求出拐點值########################
# 0-1 正規化資料
min.max.norm <- function(x){
(x-min(x))/(max(x)-min(x))
}
raw.data <- iris[,1:4]
norm.data <- data.frame(sl = min.max.norm(raw.data[,1]),
sw = min.max.norm(raw.data[,2]),
pl = min.max.norm(raw.data[,3]),
pw = min.max.norm(raw.data[,4]))
## k取2到8，評估K
K <- 2:8
round <- 30 # 每次迭代30次，避免區域性最優
rst <- sapply(K, function(i){
print(paste("K=",i))
mean(sapply(1:round,function(r){
print(paste("Round",r))
result <- kmeans(norm.data, i)
stats <- cluster.stats(dist(norm.data), result$cluster)
stats$avg.silwidth
}))
})
plot(K,rst,type='l',main='輪廓係數與K的關係', ylab='輪廓係數')
5、層次聚類得出k-means初始點
iris.hc <- hclust( dist(iris[,1:4]))
# plot( iris.hc, hang = -1)
plclust( iris.hc, labels = FALSE, hang = -1)
re <- rect.hclust(iris.hc, k = 3)
iris.id <- cutree(iris.hc, 3)######得出類別##########
6、################採用kmeans++選用k個初始點##################################
n<-length(x)
seed<-round(runif(1,1,n))
for ( i in 1:k){
if(i==1){ seed[i]<- round(runif(1,1,N)) }
dd<-0
tmp<-0
for(s in 1:n)
{
m<-length(seed)
for (j in 1:m) {
if(j==1){ tmp<-dist(x[s],seed[j]) }
else
{
tmptwo<-tmp
tmp<-dist(x[s],seed[j])
if(tmp>tmptwo)tmp<-tmptwo
}
}
dd[s]<-tmp
}
sumd<-sum(dd)
random<--round(runif(1,0, sumd))
for(ii in 1:n)
{
if(random<=0){break};
else{
random<-random-dd[ii]
}
}
seed[i+1]<-ii
}