瞎bb

noip全真模擬賽又掛了。。
出題人居然又賀了三道原題。。
T3.走向巔峰新年的葉子//原題連結
被出題人魔改之後的題面…


T1暴力T2爆蛋，，於是只好來做T3

思路

樹的多條直徑一定會相交 所以我們用最暴力的做法(去考提高的應該都會吧 先隨便選一個點 找到離這個點最遠的一些點 作為直徑的左端點們 在隨便選一個左端點找到與她最遠的一些點 也就是右端點們 然後再樹上亂搞即可)算出這段區間的左右兩個端點$p_0,p_1$

1. 如果$p_0\neq p_1$，所以就會有上面講的直徑的左端點們和右端點們，於是就在葉子結點和一堆端點之間做期望dp！然後發現只會$\theta (n^{}$
   2)\theta(n^2)的dp。。再見！！！！
2. 第一種情況$n^2$暴力但第二種情況總會好考慮一些。吧？如果$p_0=p_1$，類似於菊花圖，在$n$個葉子結點中選$m$個(最後只能剩下一個直徑的端點)簡單的$O(n)$暴力計數(求$a$個結點 還有$b(0 < b \leq a)$個結點未被染黑 再染黑一個的期望步數是$\frac{a}{b}$)！！！！！然而考後大佬又給出了反例。。。。
   
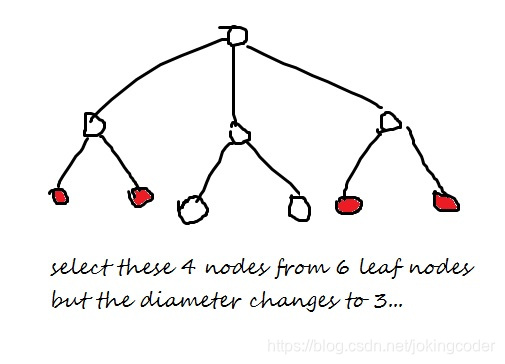
   wa的一聲就哭了。。這不是要炸的節奏嗎？？
   
   所以上面那個思路是假的

真·思路

反正出題人也搬了原題 所以我也去學(hè

1. 如果直徑的長度是偶數 那麼中點一定是在樹上的某個點上的 我們只需要把這個點拎到root上 於是幾個直徑的端點(深度為$\frac{D}{2}$)就被劃分到了幾個不同的集合 窩門只需要各個區間求期望就好了
2. 如果直徑的長度是奇數 那中點不是在樹邊上了嗎？？其實沒有關係我們假裝那有個點就好了 於是類似於第一種情況 但是發現集合只剩下兩個了

我們每次都列舉一個集合，算出其他集合全部被染黑需要的期望時間，再把這些期望時間加起來，就相當於全部的點被染黑了(集合數-1)次，所以窩門再把這個期望時間和$-$

系不繫簡單粗暴又好打ヽ(￣▽￣)ﾉ

Code

還有AC程式碼是從原來的zz程式碼魔改過來的 奇醜無比 所以大佬別打我

#include <cstdio>
#include <algorithm>
#define MOD 998244353
#define N 500005

using namespace std;
typedef long long LL;
struct Node {
	int to, nxt;
}e[N << 1];
int cnt, lst[N], d[N], du[N], st[N], maxi, leaves, tot, d1[N];
LL pre_inv[N];
LL dp[N];

inline void add(int u, int v) {
	e[++cnt].to = v;
	e[cnt].nxt = lst[u];
	lst[u] = cnt;
}

inline LL qui_pow(LL x, int y) {
	if (y == 1) return x;
	LL t = qui_pow(x, y / 2);
	if (y & 1) return t * t % MOD * x % MOD;
	else return t * t % MOD;
}

inline void dfs(int x, int fa, int dep) {
	d[x] = dep;
	if (d[x] > d[maxi]) maxi = x;
	for (int i = lst[x]; i; i = e[i].nxt) {
		if (e[i].to == fa) continue;
		dfs(e[i].to, x, dep + 1);
	}
}

inline int countt(int x, int fa, int len) {
	if (du[x] == 1 && d[x] == len) return 1;
	int sum = 0;
	for (int i = lst[x]; i; i = e[i].nxt) {
		if (e[i].to == fa) continue;
		sum += countt(e[i].to, x, len);
	}
	return sum;
}

int main() {
	int n, u, v, f = 0;
	scanf("%d", &n);
	for (int i = 1; i < n; ++i) {
		scanf("%d%d", &u, &v);
		du[u]++;
		du[v]++;
		add(u, v);
		add(v, u);
	}
	LL inv;
	for (int i = 1; i <= n; ++i) {
		inv = qui_pow(i, MOD - 2);
		pre_inv[i] = (pre_inv[i - 1] + inv) % MOD;
	}
	for (int i = 1; i <= n; ++i) {
		if (du[i] == 1) leaves++;
	}
	maxi = 0;
	dfs(1, 1, 0);
	int x = maxi;
	maxi = 0;
	dfs(x, x, 0);
	for (int i = 1; i <= n; ++i) {
		d1[i] = d[i];
	}
	x = maxi;
	maxi = 0;
	dfs(x, x, 0);
	int dia = d[maxi], mid, md, all = 0;
	if (dia & 1) {
		for (int i = 1; i <= n; ++i) {
			if (d[i] == (dia >> 1) && d1[i] == (dia >> 1) + 1) mid = i;
			if (d[i] == (dia >> 1) + 1 && d1[i] == (dia >> 1)) md = i;
		}
//		printf("%d %d\n", mid, md);
		dfs(mid, mid, 0);
		int num = countt(mid, md, (dia >> 1));
		if (num > 0) st[++tot] = num;
		all += num;
//		printf("%d\n", num);
		dfs(md, md, 0);
		num = countt(md, mid, (dia >> 1));
		if (num > 0) st[++tot] = num;
		all += num;
//		printf("%d\n", num);
	}
	else {
		for (int i = 1; i <= n; ++i) {
			if (d[i] == (dia >> 1) && d1[i] == (dia >> 1)) mid = i;
		}
		dfs(mid, mid, 0);
		for (int i = lst[mid]; i; i = e[i].nxt) {
			int num = countt(e[i].to, mid, (dia >> 1));
			if (num > 0) st[++tot] = num;
			all += num;
		}
	}
	LL ans = 0;
	for (int i = 1; i <= tot; ++i) {
		ans += pre_inv[all - st[i]];
		if (ans >= MOD) ans -= MOD;
	}
	ans -= 1LL * (tot - 1) * pre_inv[all] % MOD;
	if (ans < 0) ans += MOD;
	ans = ans * leaves % MOD;
	printf("%lld\n", ans);
	return 0;
}