Dijkstra 演算法小結
Dijkstra是圖論中用來求特定結點到其他所有結點的最短路徑長度,即單源最短路問題的演算法。
個人總結思路:
基本原理是按照最短路徑長度遞增的順序確定每一個結點的最短路徑長度,即先確定的結點的最短路徑長度不大於後確定的結點的最短路徑長度。根據結點數量進行一個大迴圈,每將一個新的結點加入已知路徑集合中,都檢查一遍所有與它相連的結點,更新從源點出發到達它們的距離向量(重要,根據結點是否在已知路徑集合中有兩種意義),選擇其中最近的結點作為新加入已知路徑集合的點並作為下次迴圈考查的結點,當所有結點考查完畢,則大迴圈結束。
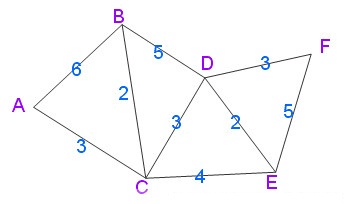

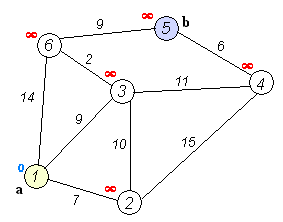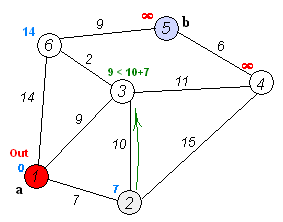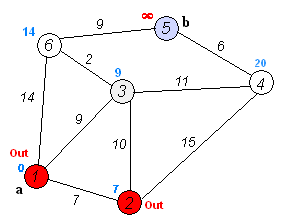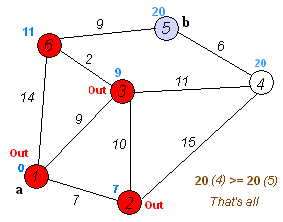
(動圖可在理解演算法之後看,或者用gif分解工具拆解後慢慢理解)
演算法流程:
(1)初始化,集合K中加入結點S,結點S到結點S本身的最短距離是0,到其他結點距離設為無窮。
(2)遍歷與集合K中結點直接相鄰的邊(U,V,C),其中U屬於集合K;V不屬於集合K。計算由源結點S出發按照已經得到的最短路到達U,再由U經過這些邊到達V時的路徑長度,選擇其中距離最短的結點作為下一個加入集合K的結點。
(3)若集合K中已經包含了所有的點,演算法結束;否則重複步驟(2)。
程式輸入輸出格式:
輸入:第一行輸入n和m,n是點數,m是無向邊數。接下來是m行,每行3個數a,b,c,表示a和b之間有一條邊,權重(長度)為c。最後一行是兩個數,起點S和終點T。n和m均為0時輸入結束。
輸出:S到T的最短距離。
#include<cstdio> #include<vector> using namespace std; struct E//鄰接連結串列中的連結串列元素結構體(U,V,C) { int next;//結點V int c;//該邊權值C }; vector<E> edge[101]; bool mark[101]; int Dis[101];//距離向量 int main() { int n,m; while(scanf("%d%d",&n,&m)!=EOF) { if(n==0&&m==0)break; for(int i=0;i<n;++i) { edge[i].clear(); Dis[i]=-1; mark[i]=false; } while(m--) { int a,b,c; scanf("%d%d%d",&a,&b,&c); E tmp; tmp.next=b; tmp.c=c; edge[a].push_back(tmp); tmp.next=a; edge[b].push_back(tmp); //將鄰接資訊加入鄰接連結串列,由於原圖為無向圖, //故每條邊資訊都要新增到其兩個頂點的兩條單鏈表中 } int S,T; scanf("%d%d",&S,&T); Dis[S]=0; mark[S]=true; int newP=S; for(int i=0;i<n;++i) { //迴圈n-1次,按照最短路徑遞增的順序確定其他n-1個點的最短路徑長度 for(int j=0;j<edge[newP].size();++j) { //遍歷與該新加入集合K中的結點直接相鄰的邊 if(mark[j]==true)continue; int t=edge[newP][j].next; int c=edge[newP][j].c; if(Dis[t]==-1||Dis[t]>Dis[newP]+c) { //若該結點尚不可達,或者該結點從新加入的結點經過一條邊到達時比以往距離更短 Dis[t]=Dis[newP]+c; } } int min=13212313;//最小值初始化為一個大整數,為找最小值做準備 for(int j=0;j<n;++j) { //遍歷所有結點,用打擂法確定要新加入集合K的點 //同時注意跳過集合K中已有的點和不可達的點 if(mark[j]==true)continue; if(Dis[j]==-1);continue; if(Dis[j]<min) { min=Dis[j]; newP=j; } } mark[newP]=true; } printf("%d\n",Dis[T]); } return 0; }
程式碼重點強調:
使用C++中STL的vector模擬鄰接連結串列,每個結點有一個vector陣列,其中儲存了該結點鄰接其它結點的(U,V,C)。vector是一個動態陣列,詳情可查手冊,當然這裡也可以用二維陣列來表示;
結點距離初始化設為-1,因為該演算法無法處理權值為負的圖,故可將-1視為無窮;
mark[i]用來表示結點i是否屬於集合K,即結點i是否已包含在得到的最短路中;
Dis[i]有兩種意義:當結點i屬於集合K時,它表示結點i已經被確定的最短路徑長度;當結點i還不屬於集合K時,它表示所有從源節點出發先按照某條最短路徑到達某已經在集合K中的結點,並由該結點經過一條邊到達結點i路徑中的最短距離
若要輸出最短路沿路經過的各個中間點,可維護一個記錄路徑中各結點前驅的陣列pred[i],表示到達i結點的最短路徑上前一個點,輸出時可倒序輸出或壓入棧中再正序輸出。
參考資料:
王道論壇 組編,《計算機考研——機試指南》,電子工業出版社
