1.小根堆
若根節點存在左子女則根節點的值小於左子女的值；若根節點存在右子女則根節點的值小於右子女的值。
2.大根堆
若根節點存在左子女則根節點的值大於左子女的值；若根節點存在右子女則根節點的值大於右子女的值。
3.結論
（1）堆是一棵完全二叉樹（如果公有h層，那麼1~h-1層均滿，在h層連續缺失若干個右葉子）。
（2）小根堆的根節點的值是最小值，大根堆的根節點的值是最大值。
（3）堆適合於採用順序儲存。
4.堆的插入演算法
將一個數據元素插入到堆中，使之依然成為一個堆。
演算法描述：先將結點插入到堆的尾部，再將該結點逐層向上調整，直到依然構成一個堆，調整方法是看每個子樹是否符合大（小）根堆的特點，不符合的話則調整葉子和根的位置。
5.堆的刪除演算法
堆在刪除元素時，只可以刪除根節點。
演算法描述：將根節點刪除後用堆尾結點進行填補，調整二叉樹，使之依然成為一個堆。
6.堆排序（大根堆，小根堆類似）
其基本思想為(大根堆)：
    1)將初始待排序關鍵字序列(R1,R2....Rn)構建成大頂堆，此堆為初始的無序區，構建的過程是每個非葉子結點都經過一次調整，調整順序為從底層至頂層(調整過程中含有遞迴)，這樣調整下來這個二叉樹整體上就是一個大根堆(或小根堆)了;

    2)將堆頂元素R[1]與最後一個元素R[n]交換，此時得到新的無序區(R1,R2,......Rn-1)和新的有序區(Rn),且滿足R[1,2...n-1]<=R[n];

    3)由於交換後新的堆頂R[1]可能違反堆的性質，因此需要對當前無序區(R1,R2,......Rn-1)調整為新堆，然後再次將R[1]與無序區最後一個元素交換，得到新的無序區(R1,R2....Rn-2)和新的有序區(Rn-1,Rn)。不斷重複此過程直到有序區的元素個數為n-1，則整個排序過程完成。
    操作過程如下：
     1)初始化堆：將R[1..n]構造為堆；

     2)將當前無序區的堆頂元素R[1]同該區間的最後一個記錄交換，然後將新的無序區調整為新的堆。

    因此對於堆排序，最重要的兩個操作就是構造初始堆和調整堆，其實構造初始堆事實上也是調整堆的過程，只不過構造初始堆是對所有的非葉節點都進行調整。
操作過程圖示：

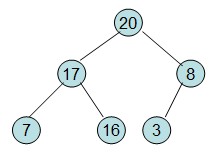
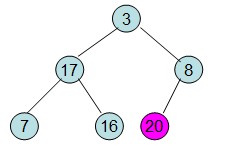
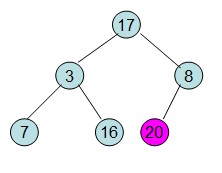
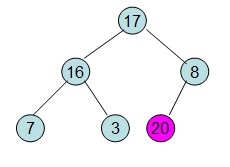
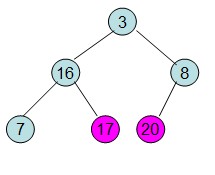
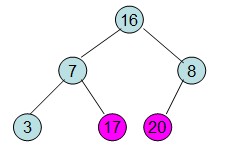
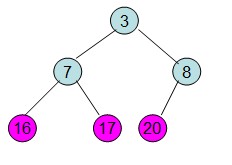
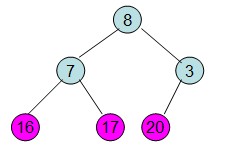
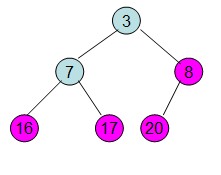
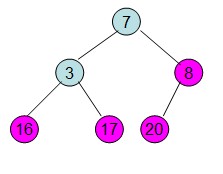
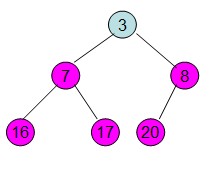
    從上述過程可知，堆排序其實也是一種選擇排序，是一種樹形選擇排序。只不過直接選擇排序中，為了從R[1...n]中選擇最大記錄，需比較n-1次，然後從R[1...n-2]中選擇最大記錄需比較n-2次。事實上這n-2次比較中有很多已經在前面的n-1次比較中已經做過，而樹形選擇排序恰好利用樹形的特點儲存了部分前面的比較結果，因此可以減少比較次數。對於n個關鍵字序列，最壞情況下每個節點需比較log2(n)次，因此其最壞情況下時間複雜度為nlog2(n)。堆排序為不穩定排序，不適合記錄較少的排序。
關於log2(n)的理解：根據堆排序的過程，每次將大根堆根節點的值跟最後一個葉子的值進行交換，那如果最後的葉子結點正好是最小的數，那麼這個葉子結點就會一層層的被放到子樹最終放到葉子結點的位子（不是前面的葉子結點的位置了），這樣的話這個葉子結點經過的層數就剛好為log2(n)。然而其他沒有交換的二叉樹的分支，因為以前都是大根堆，所以大根堆的性質還是沒有變化，這一點對理解程式至關重要。C語言程式如下：

/*堆排序(大根堆)*/ 
#include <stdio.h>

/*注意：這個函式只會在調整被交換的位置為大根堆，未交換的分支不會處理，
所以不能將一個非大根堆二叉樹的根結點傳遞過來讓這個函式將其處理為大根堆*/
void heap_ajust(int *a, int i, int size)  /*a為堆儲存陣列，size為堆的大小*/
{
    int lchild = 2*i;       //i的左孩子節點序號 
    int rchild = 2*i +1;     //i的右孩子節點序號 
    int max = i; /*存放三個頂點中最大的數的下標*/
	int temp;
    if(i <= size/2)          //如果i是葉節點就不用進行調整 
    {
        if(lchild<=size && a[lchild]>a[max])
        {
            max = lchild;
        }    
        if(rchild<=size && a[rchild]>a[max])
        {
            max = rchild;
        }
        if(max != i)
        {
            temp = a[i]; /*交換a[i]和a[max]的值*/
			a[i] = a[max];
			a[max] = temp;
            heap_ajust(a, max, size); /*被交換的位置以前是大根堆，現在可能不是大根堆
			                            所以需要重新調整使其成為大根堆結構*/ 
        }
    }        
}

void build_bheap(int *a, int size) /*建立大根堆*/ 
{
    int i;
    for(i=size/2; i >= 1; i--) /*非葉節點最大序號值為size/2*/
    {
        heap_ajust(a, i, size); /*每個非葉子結點都需要呼叫這個函式*/   
    }    
} 

void heap_sort(int *a, int size) /*堆排序*/ 
{
    int i;
	int temp;

    build_bheap(a, size);
    for(i=size; i >= 1; i--)
    {
        temp = a[1];
		a[1] = a[i];
		a[i] = temp; /*交換堆頂和最後一個元素，即每次將剩餘元素中的最大者放到最後面*/ 
        heap_ajust(a, 1, i-1); /*重新調整堆頂節點成為大頂堆，只有被交換的分支才有可能不是大根堆*/
    }
} 

int main(int argc, char *argv[])
{
    int a[]={0,16,20,3,11,17,8};
    int size = sizeof(a)/sizeof(int) -1;
	int i;

	printf("size = %d\n", size);
    heap_sort(a, size);
	printf("Sort over:"); 
    for(i=1;i <= size; i++)
        printf("%d ", a[i]);
    printf("\n");

    return 0;
}

程式執行截圖為：

參考博文地址：http://www.cnblogs.com/dolphin0520/archive/2011/10/06/2199741.html