數字訊號處理實驗(一):離散時間訊號和系統的時域分析
阿新 • • 發佈:2019-01-07
目錄
一、實驗目的:
熟悉Mat lab中產生訊號和繪製訊號的基本命令,掌握產生離散時間訊號的基本方法;掌握離散時間系統對輸入訊號的簡單運算處理,驗證離散時間系統有關特性。
二、實驗內容及要求:
1. 離散時間訊號的時域分析:
(1)修改程式P1.1,產生單位抽樣序列並繪圖。
(2)修改程式P1.1,產生單位步長序列並繪圖。
(3)修改程式P1.4,產生長度為50、頻率為0.08、振幅為2.5、相移為90度的一個正弦序列並繪圖,該序列的週期是多少?
2. 離散時間系統的時域分析:
(1)修改程式P2.3,其中a=4, b=-6, 並繪圖,該離散時間系統是線性嗎?
(2)修改程式P2.4,其中D=15, 並繪圖,該離散時間系統是時不變嗎?
(3)修改程式P2.5,產生如下因果線性時不變系統的衝激響應的前45個樣本並繪圖:
(4)執行程式P2.7,對序列和求卷積生成,並用FIR濾波器對輸入濾波,求得;和有差別嗎?為什麼要使用對補零後得到的作為輸入來產生?
三、實驗結果及問題回答:
1. 離散時間訊號的時域分析:
(1)實驗結果:
clf;
n=-10:20;
u=[zeros(1,11) zeros(1,10) 1 zeros(1,9)];%產生向右移動了11個單位的衝激訊號
stem(n,u);
xlabel('時間序號 n');
ylabel('振幅');
title('單位樣本序列')
axis([-10 20 0 1.2])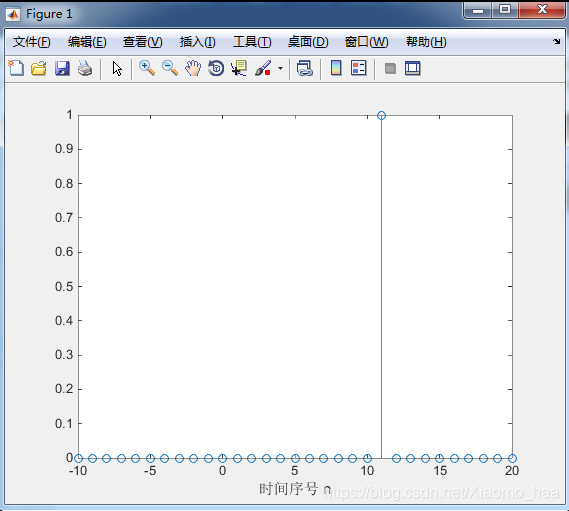
2)實驗結果:
clf; n=-10:20; u=[zeros(1,3) ones(1,28)];%產生向左移動了7個單位的階躍訊號 stem(n,u); xlabel('時間序號 n'); yalbel('振幅'); title('單位樣本序列') axis([-10 20 0 1.2])
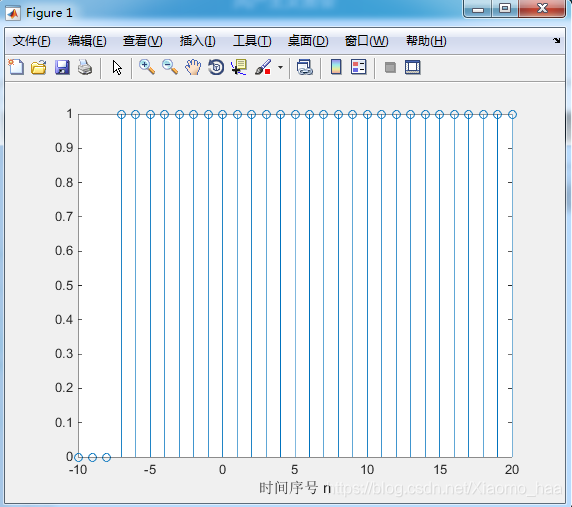
(3)實驗結果:
clf;
n=0:50;
f=0.08;%定義訊號的頻率
phase=pi/2;%定義訊號的相位
A=2.5;%定義訊號的幅度
arg=2*pi*f*n-phase;
x=A*cos(arg);%生成訊號
stem(n,x)
axis([0 40 -3 3])
grid on

該序列的週期是12.5;
2. 離散時間系統的時域分析:
(1)實驗結果:
clf;
n=0:40;
a=4;
b=-6;
x1=cos(2*pi*0.2*n);%生成訊號x1
x2=cos(2*pi*0.8*n);%生成訊號x2
x=a*x1+b*x2;%線形組合
num=[2.2403 2.4908 2.2403];%差分方程輸入訊號的係數
den=[1 -0.4 0.75];%差分方程輸出訊號的係數
ic=[0 0];
y1=filter(num,den,x1,ic);%對x1進行濾波
y2=filter(num,den,x2,ic);%對x2進行濾波
y=filter(num,den,x,ic);%對x進行濾波
yt=a*y1+b*y2;%線形組合
d=y-yt;%求出兩個訊號的差值
subplot(311)
stem(n,y);
ylabel('振幅');
title('加權輸入:y');
subplot(312)
stem(n,yt);
ylabel('振幅');
title('加權輸出:yt');
subplot(313);
stem(n,d);
xlabel('時間序號n');
ylabel('振幅');
title('差訊號:d');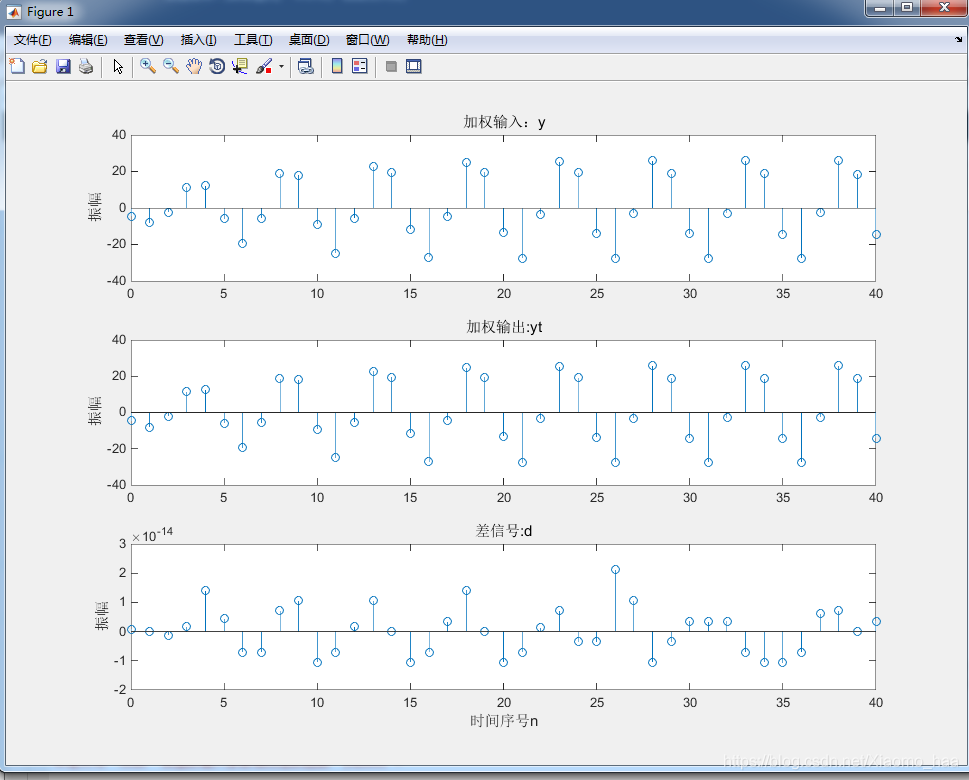
雖然最後得到的差值不為0,但是差值的數值都比較小,所以我麼可以認為差值都是0,所以這個系統是線性系統。
(2)實驗結果:
clf;
n=0:40;
D=15;
a=3.0;
b=-2;
x=a*cos(2*pi*0.2*n)+b*cos(2*pi*0.8*n);%生成原始訊號x
xd=[zeros(1,D) x];
num=[2.2403 2.4908 2.2403];%定義函式的分子向量
den=[1 -0.4 0.75];%定義函式的分母向量
ic=[0 0];
y=filter(num,den,x,ic);%對x進行濾波
yd=filter(num,den,xd,ic);%對xd進行濾波
d=y-yd(1+D:41+D);%求出兩個訊號差值
subplot(311)
stem(n,y);
ylabel('振幅')
title('輸出')
subplot(312)
stem(n,yd(1:41));
ylabel('振幅')
title('由於延時輸入的輸出')
grid on;
subplot(313)
stem(n,d);
xlabel('時間序號n')
yalbel('振幅')
title('差值訊號')
grid on
由圖可以看出,差值為0,即對原來的系統輸入延時之後,輸出沒有發生變化,所以該系統是時不變系統。
(3)實驗結果:
clf;
N=45;
num=[0.9 -0.45 0.35 0.002];%定義函式的分子向量
den=[1 0.71 -0.46 -0.62];%定義函式的分母向量
y=impz(num,den,N);%求函式的衝激響應
stem(y);
xlable('上時間序號n');
ylabel('振幅');
title('衝激響應');
grid on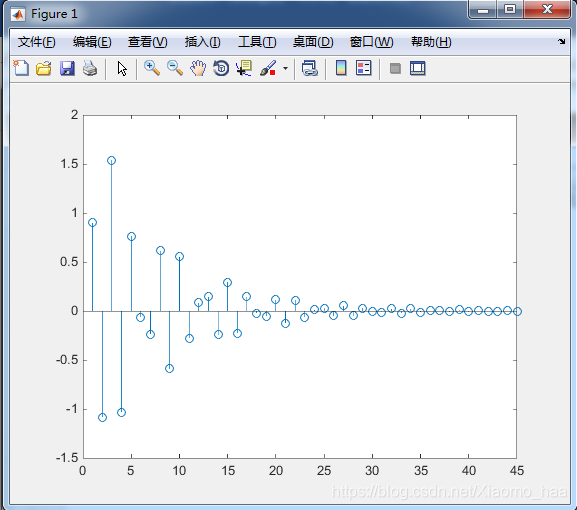
(4)實驗結果:
clf;
h=[3 2 1 -2 1 0 -4 0 3];%定義序列h
x=[1 -2 3 -4 3 2 1];%定義序列x
y=conv(h,x);%求序列h和x的卷積
n=0:14;
subplot(211)
stem(n,y);
xlabel('時間序號n');
ylabel('振幅');
title('用卷積得到的輸出yn');
grid on
x1=[x zeros(1,8)];%生成訊號x1
y1=filter(h,1,x1);%對序列x1進行濾波
subplot(212)
stem(n,y1);
xlabel('時間序號n');
ylabel('振幅');
title('由濾波生成的輸出y1n');
grid on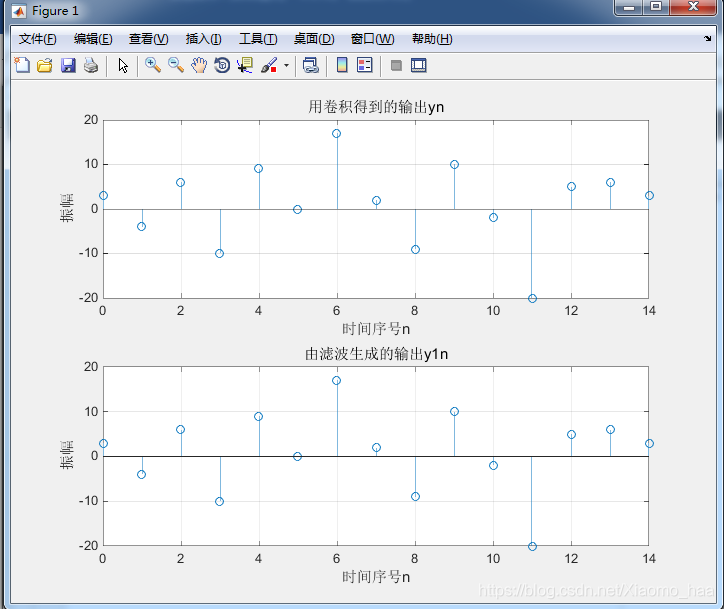
y(n)和y1(n)沒有差別。因為濾波函式生成的的訊號長度和輸入訊號的長度一致,而卷積運算中輸出訊號的長度是輸入訊號的長度和衝激響應的訊號的長度之和減去1,為了使二者一樣,就要對x(n)補零之後再作為輸入來產生y1(n)。
