Stanford機器學習---第十二講.推薦系統
阿新 • • 發佈：2019-01-07
本節簡單介紹一下上述演算法的矩陣表示方法，知道這個可以幫助我們理解該演算法線性代數層面上的矩陣或向量表達，從而在實際應用中快速程式設計實現演算法。
一、演算法的矩陣表示
如下圖，我們可以把使用者的評分，即訓練資料的ground truth，放在一個大的Y矩陣裡儲存下來
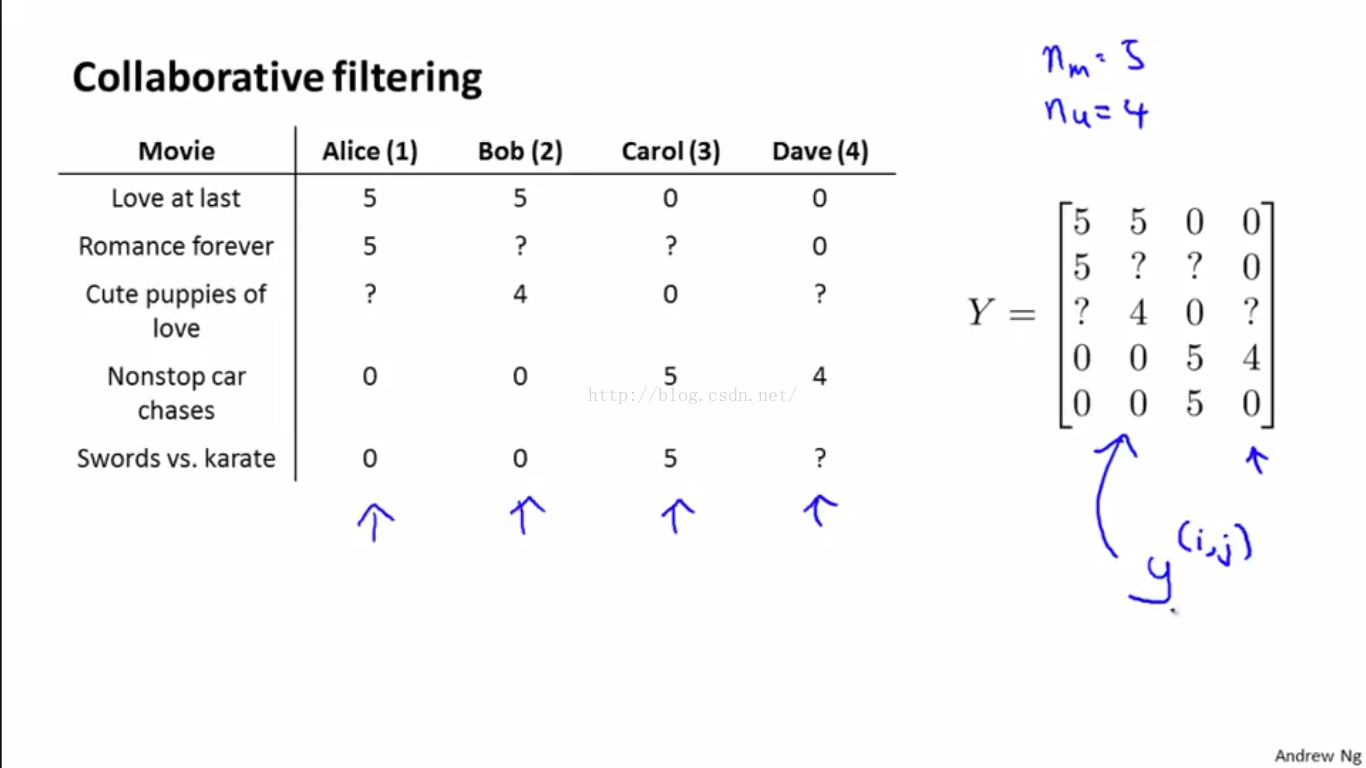
而預測結果用矩陣表示則如下：
將右側矩陣轉化成矩陣乘積的形式，如下：
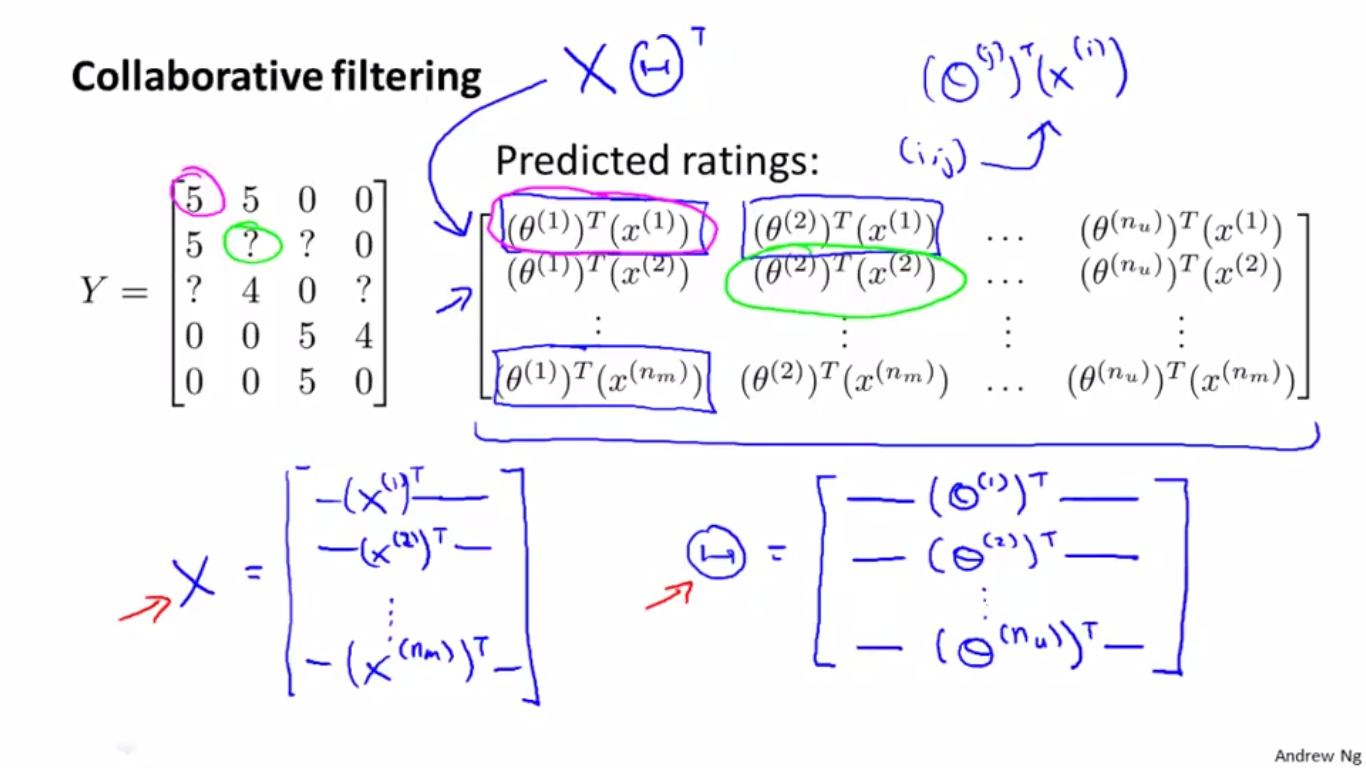寫成這種矩陣乘積的形式以後，就便於用程式語言實現演算法了。
二、電影相關性
對模型以及資料矩陣化或者向量化表達以後，我們再探討計算電影相關性的問題，就方便多了。
思想很簡單：
我們上面已經介紹過用向量 x 來描述電影的內容、屬性等，那麼 x 就可以作為電影的特徵向量。兩個向量差的模值、範數等，都可以用來描述兩部電影的相似度、相關性。so easy～
三、均值向量規範化
這是一個實現演算法的小的技術細節問題，下面我們來簡單闡述一下。
1、Problem Motivation
先來說說提出“均值向量規範化”這個技術細節的動機。如下圖所示：
當第5個使用者 Eve 對所有電影都沒有評價時，r(i, 5) 全部是0。所以當j=5時目標函式的第一項不存在，即為0。優化問題就變成了使上圖公式的最後一項最小，得到的解便是%7D "\theta^{(5)}")
的所有項均為0，則與任意 x 向量相乘的結果也均為0。這不是我們想要的，這樣的學習和預測結果都是毫無意義的。
2、用均值向量規範化來解決上述問題
具體如下圖：
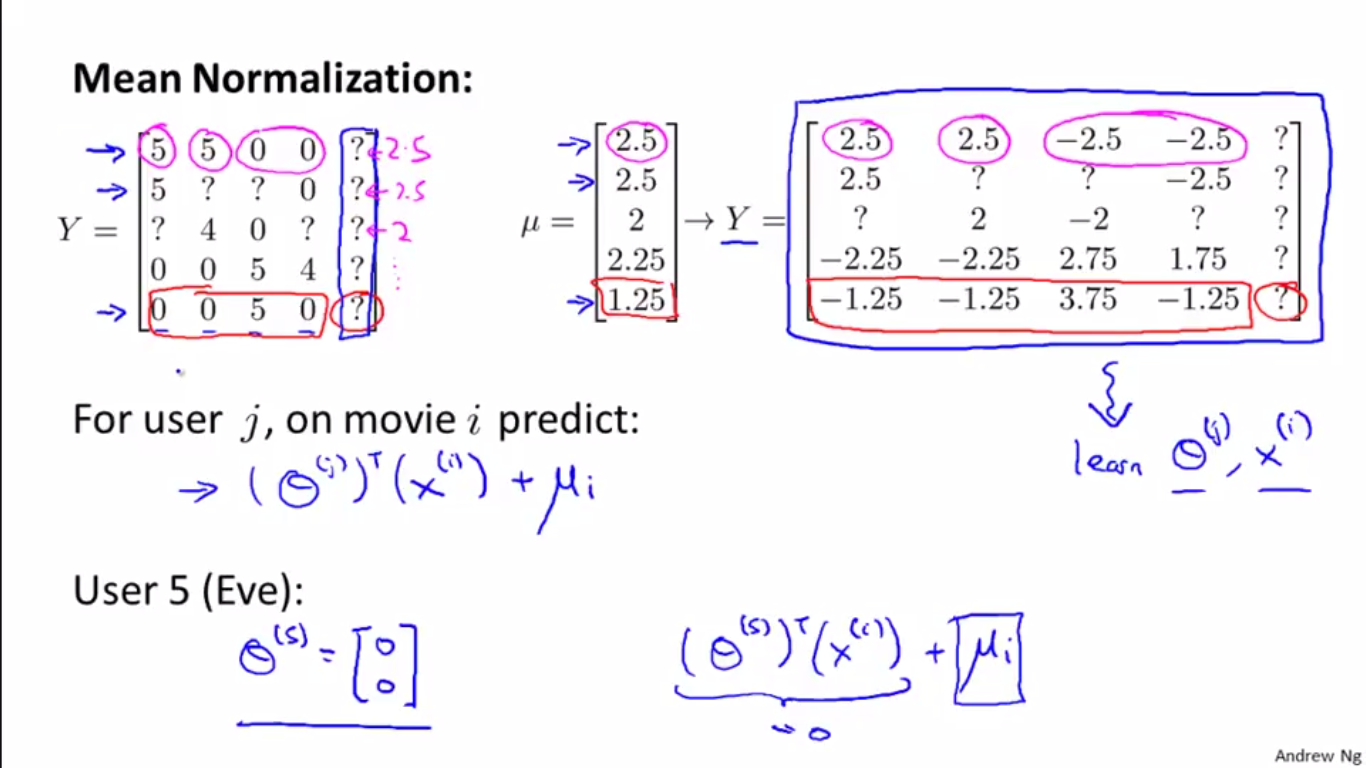
（1）計算均值向量：計算每部電影的平均得分（沒打分的問號處不計算在內），得到五部電影的平均得分向量。
（2）均值向量規範化：然後用分數矩陣Y減去該向量，得到上圖右側的新矩陣Y。
（3）訓練：將新的Y矩陣作為訓練資料，學習 x 和 theta。
（4）預測：與之前不同的是，這時預測需要重新加上均值向量：
例如，學習得到的使用者 Eve 的特徵向量，元素仍然全部為0，但是因為要加上均值向量計算評分，所以預測結果自然不會是0了。
分析說明：
一、演算法的矩陣表示
如下圖，我們可以把使用者的評分，即訓練資料的ground truth，放在一個大的Y矩陣裡儲存下來
而預測結果用矩陣表示則如下：
將右側矩陣轉化成矩陣乘積的形式，如下：
寫成這種矩陣乘積的形式以後，就便於用程式語言實現演算法了。二、電影相關性
對模型以及資料矩陣化或者向量化表達以後，我們再探討計算電影相關性的問題，就方便多了。
思想很簡單：
我們上面已經介紹過用向量 x 來描述電影的內容、屬性等，那麼 x 就可以作為電影的特徵向量。兩個向量差的模值、範數等，都可以用來描述兩部電影的相似度、相關性。so easy～
三、均值向量規範化
這是一個實現演算法的小的技術細節問題，下面我們來簡單闡述一下。
1、Problem Motivation
先來說說提出“均值向量規範化”這個技術細節的動機。如下圖所示：
當第5個使用者 Eve 對所有電影都沒有評價時，r(i, 5) 全部是0。所以當j=5時目標函式的第一項不存在，即為0。優化問題就變成了使上圖公式的最後一項最小，得到的解便是
2、用均值向量規範化來解決上述問題
具體如下圖：
（1）計算均值向量：計算每部電影的平均得分（沒打分的問號處不計算在內），得到五部電影的平均得分向量。
（2）均值向量規範化：然後用分數矩陣Y減去該向量，得到上圖右側的新矩陣Y。
（3）訓練：將新的Y矩陣作為訓練資料，學習 x 和 theta。
（4）預測：與之前不同的是，這時預測需要重新加上均值向量：
例如，學習得到的使用者 Eve 的特徵向量，元素仍然全部為0，但是因為要加上均值向量計算評分，所以預測結果自然不會是0了。
分析說明：