Stanford機器學習---第八講. 支援向量機SVM
本欄目(Machine learning)包括單引數的線性迴歸、多引數的線性迴歸、Octave Tutorial、Logistic Regression、Regularization、神經網路、機器學習系統設計、SVM(Support Vector Machines 支援向量機)、聚類、降維、異常檢測、大規模機器學習等章節。所有內容均來自Standford公開課machine learning中Andrew老師的講解。(https://class.coursera.org/ml/class/index)
第八講. 支援向量機進行機器學習——Support Vector Machine
===============================
(一)、SVM 的 Cost Function
(二)、SVM —— Large Margin Classifier
(三)、數學角度解析為什麼SVM 能形成 Large Margin Classifier(選看)
(四)、SVM Kernel 1 —— Gaussian Kernel
(五)、SVM 中 Gaussian Kernel 的使用
(六)、SVM的使用與選擇
本章內容為支援向量機Support Vector Machine(SVM)的導論性講解,在一般機器學習模型的理解上,引入SVM的概念。原先很多人,也包括我自己覺得SVM是個很神奇的概念,讀完本文你會覺得,其實只是擁有不同的目標函式, 不同的模型而已,Machine Learning的本質還沒有變,呵呵~
完成本文花了我很長時間,為了搞懂後面還有程式方便和參考網站大家實驗,希望對大家有所幫助。
=====================================
(一)、SVM 的 Cost Function
前面的幾章中我們分別就linear regression、logistic regression以及神經網路的cost function進行了講解。這裡我們通過logistic regression的cost function引入SVM。
首先回憶一下logistic regression的模型:
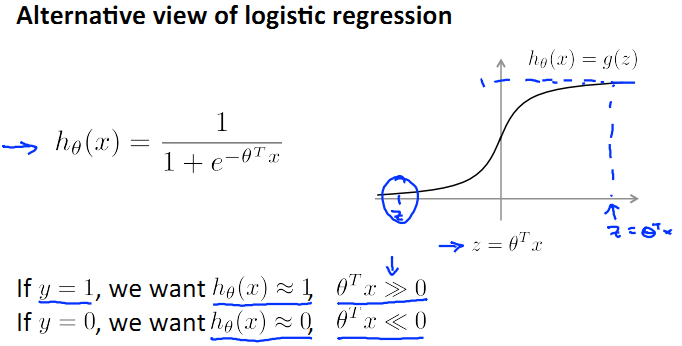
還是原先的假設,suppose我們只有兩個類,y=0和y=1。那麼根據上圖h(x)的圖形我們可以看出,
當y=1時,希望h(x)≈1,即z>>0;
當y=0時,希望h(x)≈0,即z<<0;
那麼邏輯迴歸的cost function公式如下:
cost function我們之前已經講過了,這裡不予贅述。現在呢,我們來看看下面的兩幅圖,這兩幅圖中灰色的curve是logistic regression的cost function分別取y=1和y=0的情況,
y=1時,隨著z↑,h(x)逐漸逼近1,cost逐漸減小。
y=0時,隨著z↓,h(x)逐漸逼近0,cost逐漸減小。
這正是圖中灰色曲線所示的曲線。
ok,現在我們來看看SVM中cost function的定義。請看下圖中玫瑰色的曲線,這就是我們希望得到的cost function曲線,和logistic regression的cost function非常相近,但是分為兩部分,下面呢,我們將對這個cost function進行詳細講解。
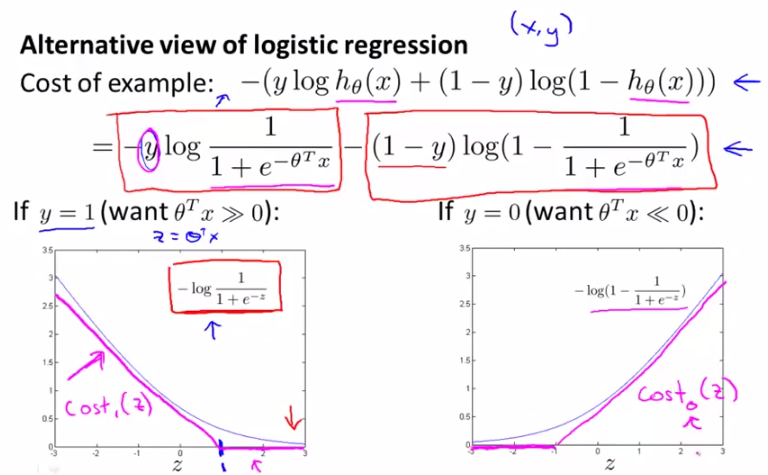
logistic regression的cost function:
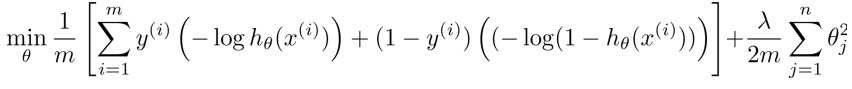
現在呢,我們給出SVM的目標函式(cost function)定義:
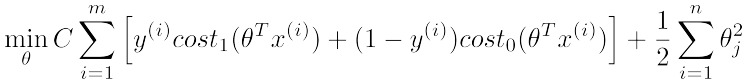
該式中,cost0和cost1分別對應y=0和y=1時的目標函式定義,最後一項regularization項和logistic regression中的類似。感覺係數少了什麼?是的,其實它們的最後一項本來是一樣的,但是可以通過線性變換化簡得到SVM的歸一化項。
=====================================
(二)、SVM —— Large Margin Classifier
本節給出一個簡單的結論——SVM是一個large margin classifier。什麼是margin呢?下面我們做詳細講解,其理論證明將在下一節中給出。
在引入margin之前,我們回顧一下上一節中的SVM cost function curve,如下圖所示分別是y取1和0時的情況。先給出一個結論,常數C取一個很大的值比較好(比如100000),這是為什麼呢?
我們來看哈,C很大,就要求[]中的那部分很小(令[]中的那部分表示為W),不如令其為0,這時來分析裡面的式子:
※需求1:
y=1時,W只有前一項,令W=0,就要求Cost1(θTx)=0,由右圖可知,這要求θTx>=1;
y=0時,W只有後一項,令W=0,就要求Cost0(θTx)=0,由右圖可知,這要求θTx<=-1;
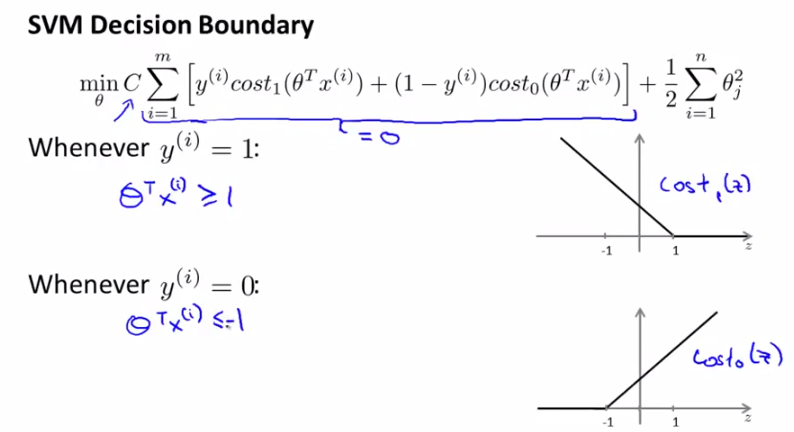
由以上說明可知,對C的取值應該在分類是否犯錯和margin的大小上做一個平衡。那麼C取較大的值會帶來什麼效果呢?就是我們開頭說的結論——SVM是一個large margin classifier。那麼什麼是margin?在第三章中我們已經講過了decision boundary,它是能夠將所有資料點進行很好地分類的h(x)邊界。如下圖所示,我們可以把綠線、粉線、藍線或者黑線中的任意一條線當做decision boundary,但是哪一條最好呢?這裡我們可以看出,綠色、粉色、藍色這三類boundary離資料非常近,i.e.我們再加進去幾個資料點,很有可能這個boundary就能很好的進行分類了,而黑色的decision boundary距離兩個類都相對較遠,我們希望獲得的就是這樣的一個decision boundary。margin呢,就是將該boundary進行平移所得到的兩條藍線的距離,如圖中所指。

相對比:
C小,decision boundary則呈現為黑線;若C很大,就呈現粉線;
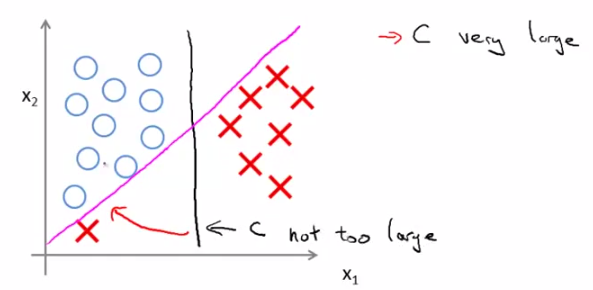
這個結論大家可以記住,也可以進行數學上的分析,下一節中我們將從數學角度分析,為什麼SVM選用大valeu的C會形成一個large margin classifier。
再給出一個數學上對geometry margin的說明:

任意一個點x到分類平面的距離γ的表示如上圖所示,其中y是{+1,-1}表示分類結果,x0是分類面上距x最短的點,分類平面的方程為wx+b=0,將x0帶入該方程就有上面的結果了。對於一個數據集x,margin就是這個資料及所有點的margin中離hyperplane最近的距離,SVM的目的就是找到最大margin的hyperplane。
練習:

=====================================
(三)、數學角度解析為什麼SVM 能形成 Large Margin Classifier(選看)
這一節主要為了證明上一節中的結論,為什麼SVM是Large Margin Classification,能形成很好的decision boundary,如果僅僅處於應用角度考慮的朋友可以略過此節。首先我們來看兩個向量內積的表現形式。假設向量u,v均為二維向量,我們知道u,v的內積uTv=u1v1+u2v2。表現在座標上呢,就如下圖左邊所示:
首先將v投影至u向量,記其長度為p(有正負,與u同向為正,反相為負,標量),則兩向量的內積uTv = ||u|| · ||v|| · cosθ = ||u|| · p = u1v1+u2v2。
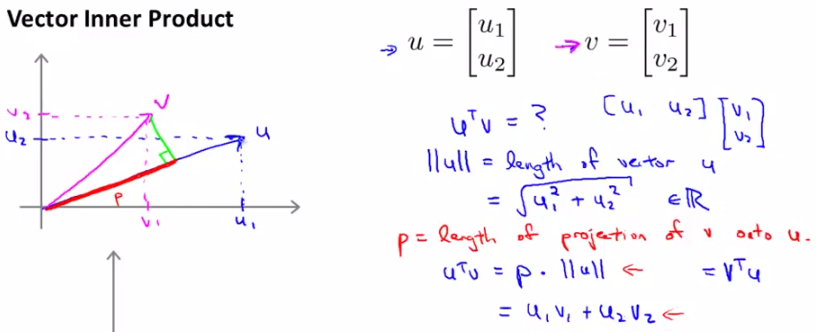
這樣一來,我們來看SVM的cost function:
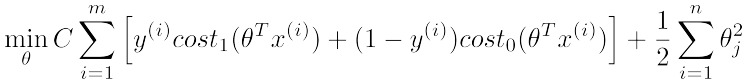
由於將C設的很大,cost function只剩下後面的那項。採取簡化形式,意在說明問題即可,設θ0=0,只剩下θ1和θ2,
則cost function J(θ)=1/2×||θ||^2
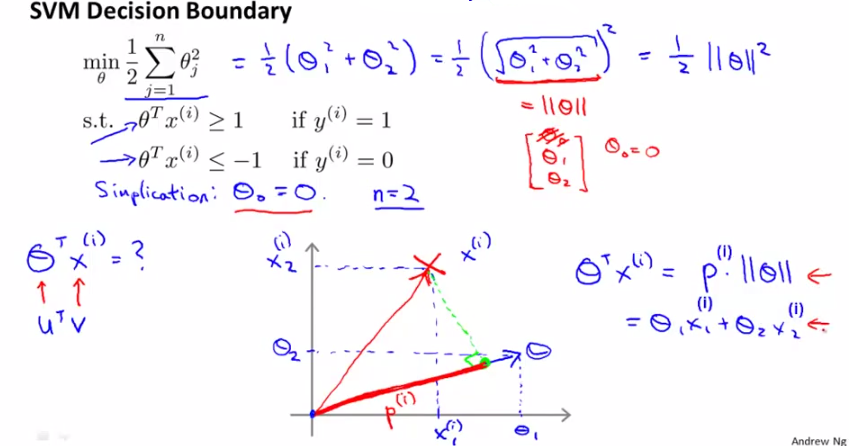
而根據上面的推導,有θTx=p·||θ||,其中p是x在θ上的投影,則
※需求2:
y=1時,W只有前一項,令W=0,就要求Cost1(θTx)=0,由右圖可知,這要求p·||θ||>=1;
y=0時,W只有後一項,令W=0,就要求Cost0(θTx)=0,由右圖可知,這要求p·||θ||<=-1;
如下圖所示:
我們集中精力看為什麼SVM的decision boundary有large margin(這裡稍微有點兒複雜,好好看哈):
對於一個給定資料集,依舊用X表示正樣本,O表示負樣本,綠色的線表示decision boundary,藍色的線表示θ向量的方向,玫瑰色表示資料在θ上的投影。
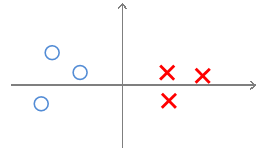
我們已知boundary的角度和θ向量呈的是90°角(自己畫一下就知道了)。
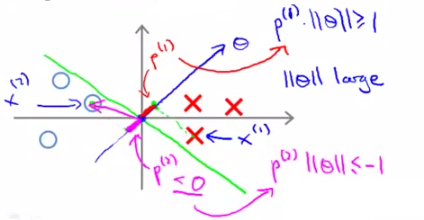
先看這個圖,對於這樣一個decision boundary(沒有large margin),θ與其呈90°角如圖所示,這樣我們可以畫出資料集X和O在θ上的投影,如圖所示,非常小;如果想滿足[需求2]中說的
對正樣本p·||θ||>=1,
對負樣本p·||θ||<=-1,
就需要令||θ||很大,這就和cost function的願望(min 1/2×||θ||^2)相違背了,因此SVM的不出來這個圖中所示的decision boundary結果。
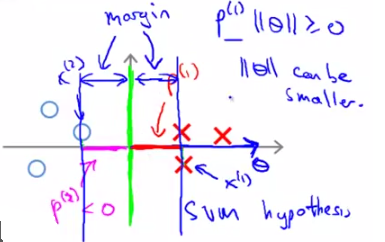
那麼再來看下面這個圖,
它選取了上一節中我們定義的“比較好的”decision boundary,兩邊的margin都比較大。看一下兩邊資料到θ的投影,都比較大,這樣就可以使||θ||相對較小,滿足SVM的cost function。因此按照SVM的cost function進行求解(optimization)得出的decision boundary一定是有large margin的。說明白了吧?!
練習:

分析:由圖中我們可以看出,decision boundary的最優解是y=x1,這時所有資料集中的資料到θ上的投影最小值為2,換言之,想滿足
對正樣本p·||θ||>=1,
對負樣本p·||θ||<=-1,
只需要
對正樣本2·||θ||>=1,
對負樣本(-2)·||θ||<=-1,
因此需要||θ||>=1/2,本著令cost function最小的原則,我們可知||θ||=1/2.=====================================
(四)、SVM Kernel 1 —— Gaussian Kernel
對於一個非線性Decision boundary,我們之前利用多項式擬合的方法進行預測:
- f1, f2, ... fn為提取出來的features。
- 定義預測方程hθ(x)為多項式的sigmod函式值:hθ(x)=g(θ0f0+θ1f1+…+θnfn),其中fn為x的冪次項組合(如下圖)
- 當θ0f0+θ1f1+…+θnfn>=0時hθ(x)=1;else hθ(x)=0;
那麼,除了將fn定義為x的冪次項組合,還有沒有其他方法表示 f 呢?本節就引入了Kernel,核的概念。即用核函式表示f。
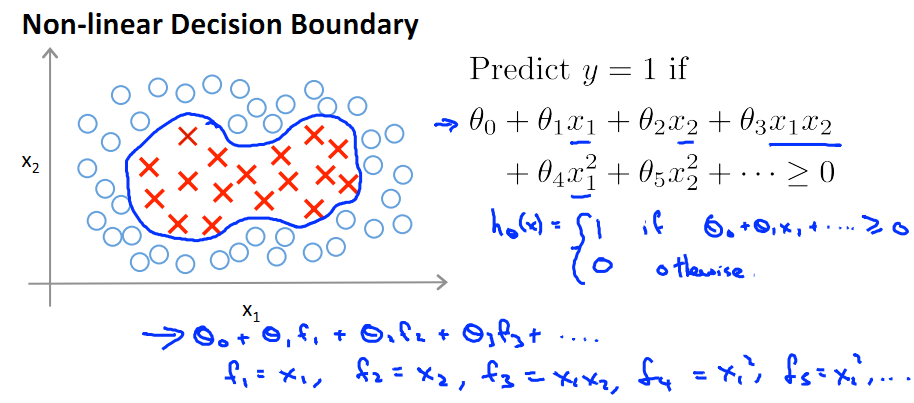
對於上圖的非線性擬合,我們通過計算輸入原始向量與landmark之間的相似度來計算核值f:

發現相似度計算公式很像正態分佈(高斯分佈)對不對?是的!這就是高斯核函式。由下圖可以看出,
x和l越相似,f越接近於1;
x與l相差越遠,f越接近於0;
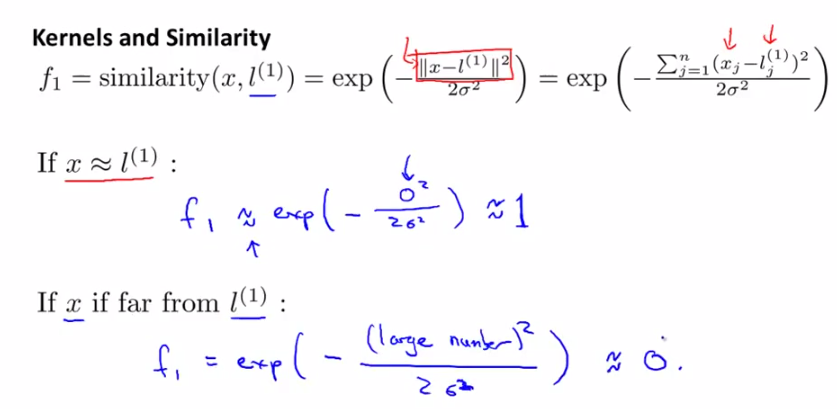
下圖中的橫縱座標為x的兩個維度值,高為f(new feature)。制高點為x=l的情況,此時f=1。
隨著x與l的遠離,f逐漸下降,趨近於0.
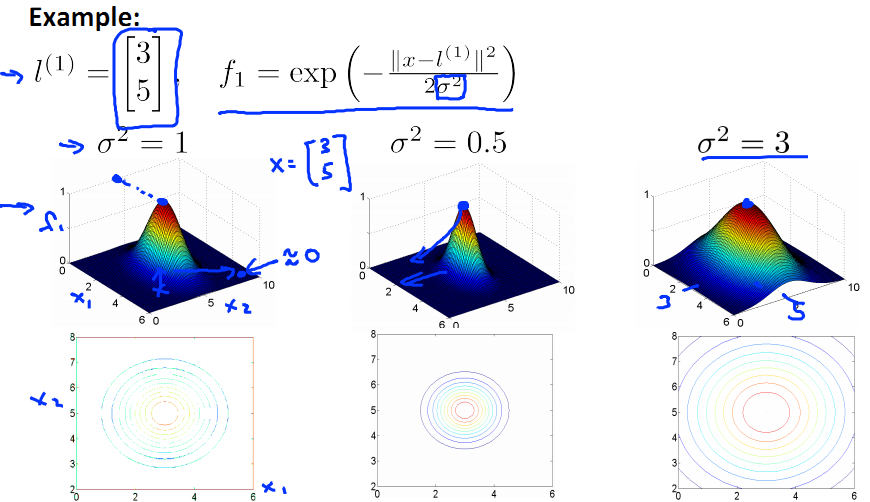
下面我們來看SVM核分類預測的結果:
引入核函式後,代數上的區別在於f變了,原來f是x1/x1^2/...,即xi冪次項乘積
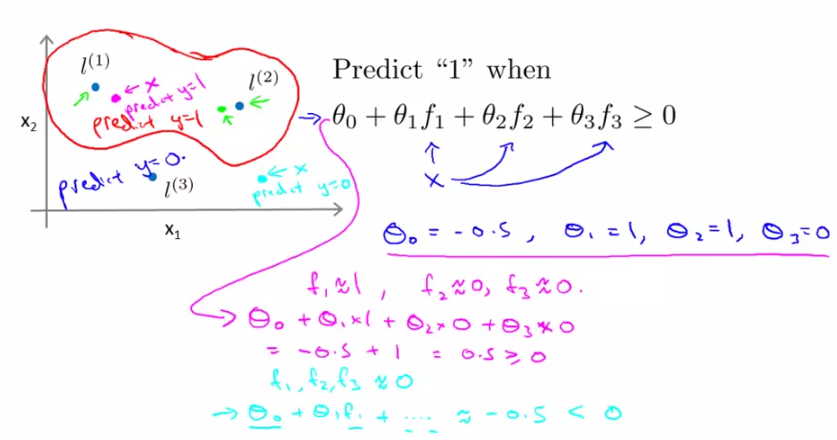
引入核函式後,幾何上來說可以更直觀的表示是否應該歸為該類了(如下圖)
- 比如我們想將座標上的所有資料點分為兩類(如下圖中)紅色圈內希望預測為y=1;圈外希望預測為y=0。通過訓練資料集呢,我們得到了一組θ值(θ0,θ1,θ2,θ3)=(-0.5,1,1,0)以及三個點(L1,L2,L3),(具體怎麼訓練而成的大家先不要過分糾結,後面會講)
- 對於每個test資料集中的點,我們首先計算它到(L1,L2,L3)各自的相似度,也就是核函式的值(f1,f2,f3),然後帶入多項式θ0f0+θ1f1+…+θnfn計算,當它>=0時,預測結果為類內點(正樣本,y=1),else預測為負樣本,y=0
=====================================
(五)、SVM 中 Gaussian Kernel 的使用
§5.1. landmark的選取和引數向量θ的求解
上一節中我們遺留了兩個問題,一個是一些L點的選取,一個是向量θ計算。這一節我們就來講講這兩個問題。
首先來看L的選取。上一節中一提到Gaussian kernel fi 的計算:
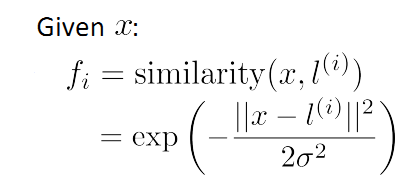
這裡呢,我們選擇m個訓練資料,並取這m個訓練資料為m個landmark(L)點(不考慮證樣本還是負樣本),如下圖所示:
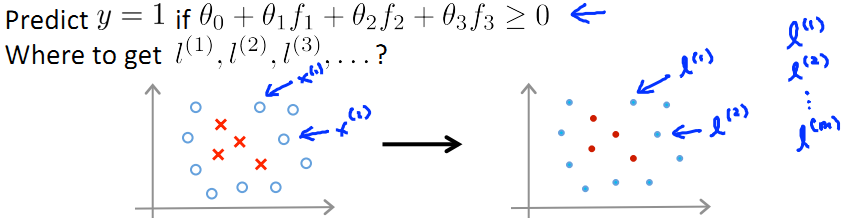

PS:那麼在這m個訓練資料中,每一個訓練資料x(i)所得的特徵向量(核函式)f中,總有一維向量的值為1(因為這裡x(i)=l(i))
於是,每個特徵向量f有m+1維(m維訓練資料[f1,f2,...,fm]附加一維f0=1)
在SVM的訓練中,將Gaussian Kernel帶入cost function,通過最小化該函式就可與得到引數θ,並根據該引數θ進行預測:
若θTf>=0,predicty=1;
else predict y=0;
如下圖所示,這裡與之前講過的cost function的區別在於用kernel f 代替了x。

§5.2. landmark的選取和引數向量θ的求解
好了,至此Landmark點和θ的求取都解決了,還有一個問題,就是cost function中兩個引數的確定:C和σ2。
對於C,由於C=1/λ,所以
C大,λ小,overfit,產生low bias,high variance
C小,λ大,underfit,產生high bias,low variance
詳細原因請參考第六章中關於bias和variance的講解。
對於方差σ2,和正態分佈中的定義一樣,
σ2大,x-f 影象較為扁平;
σ2小,x-f 影象較為窄尖;

關於C和σ2的選取,我們來做個練習:
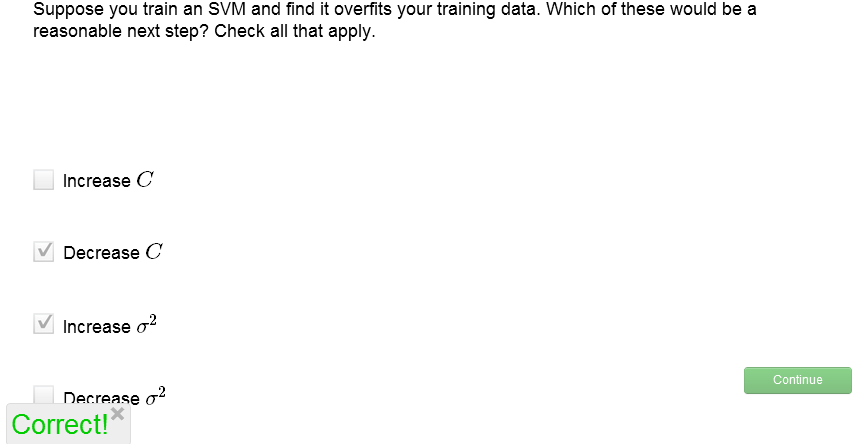
解析,過擬合說明應該適當加強cost function中的正則項所起的作用,因此應增大λ,即減小C;同時,過擬合是的只有一小部分範圍內的x享有較大f,或者說x的覆蓋面太窄了,所以應當增大σ2。
=====================================
(六)、SVM 的 使用與選擇
本節中主要介紹SVM在matlab中用libsvm中的應用,給大家一個用SVM進行實踐的平臺。
前面幾節中我們已知用SVM進行機器學習的過程就是一個optimize引數θ的過程,這裡呢,我們首先介紹一個Chih-Chung Chang 和 Chih-Jen Lin做的 matlab/C/Ruby/Python/Java...中通用的機器學習tool,libsvm,其基本講解和測試我以前講過(在這裡),算是入門篇,並不詳細,這裡呢,我們將結合本章課程近一步學習,並用matlab實現。
首先大家來看看,想要進行SVM學習,有哪兩類:
一種是No kernel(linear kernel),hθ(x)=g(θ0x0+θ1x1+…+θnxn),predict y=1 if θTx>=0;
另一種是使用kernel f(比如Gaussian Kernel),hθ(x)=g(θ0f0+θ1f1+…+θnfn),這裡需要選擇方差引數σ2
如下圖所示:

需要注意的是,不管用那種方法,都需要在ML之前進行Normalization歸一化!
當然,除了Gaussian kernel,我們還有很多其他的kernel可以用,比如polynomial kernel等,如下圖所示,但andrew表示他本人不會經常去用(或者幾乎不用)以下"more esoteric"中的核,一個原因是其他的核不一定起作用。我們講一下polynomial kernel:
polynomial 核形如 K(x,l)= (xTl+c)d,也用來表示兩個object的相似度

首先給大家引入一個資料集,在該資料集中,我們可以進行初步的libsvm訓練和預測,如這篇文章中所說,這個也是最基本的no kernel(linear kernel)。
然後呢,給大家一個reference,這是libsvm中traing基本的語法:
Usage: model = svmtrain(training_label_vector, training_instance_matrix, 'libsvm_options');
libsvm_options:
-s svm_type : set type of SVM (default 0)
0 -- C-SVC
1 -- nu-SVC
2 -- one-class SVM
3 -- epsilon-SVR
4 -- nu-SVR
-t kernel_type : set type of kernel function (default 2)
0 -- linear: u'*v
1 -- polynomial: (gamma*u'*v + coef0)^degree
2 -- radial basis function: exp(-gamma*|u-v|^2)
3 -- sigmoid: tanh(gamma*u'*v + coef0)
4 -- precomputed kernel (kernel values in training_instance_matrix)
-d degree : set degree in kernel function (default 3)
-g gamma : set gamma in kernel function (default 1/num_features)
-r coef0 : set coef0 in kernel function (default 0)
-c cost : set the parameter C of C-SVC, epsilon-SVR, and nu-SVR (default 1)
-n nu : set the parameter nu of nu-SVC, one-class SVM, and nu-SVR (default 0.5)
-p epsilon : set the epsilon in loss function of epsilon-SVR (default 0.1)
-m cachesize : set cache memory size in MB (default 100)
-e epsilon : set tolerance of termination criterion (default 0.001)
-h shrinking : whether to use the shrinking heuristics, 0 or 1 (default 1)
-b probability_estimates : whether to train a SVC or SVR model for probability estimates, 0 or 1 (default 0)
-wi weight : set the parameter C of class i to weight*C, for C-SVC (default 1)
-v n : n-fold cross validation mode
-q : quiet mode (no outputs)下面給大家一個例子:
function [ output_args ] = Nonlinear_SVM( input_args )
%NONLINEAR_SVM Summary of this function goes here
% Detailed explanation goes here
%generate data1
r=sqrt(rand(100,1));%generate 100 random radius
t=2*pi*rand(100,1);%generate 100 random angles, in range [0,2*pi]
data1=[r.*cos(t),r.*sin(t)];%points
%generate data2
r2=sqrt(3*rand(100,1)+1);%generate 100 random radius
t2=2*pi*rand(100,1);%generate 100 random angles, in range [0,2*pi]
data2=[r2.*cos(t2),r2.*sin(t2)];%points
%plot datas
plot(data1(:,1),data1(:,2),'r.')
hold on
plot(data2(:,1),data2(:,2),'b.')
ezpolar(@(x)1);%在極座標下畫ρ=1,θ∈[0,2π]的影象,即x^2+y^2=1
ezpolar(@(x)2);
axis equal %make x and y axis with equal scalar
hold off
%build a vector for classification
data=[data1;data2]; %merge the two dataset into one
datalabel=ones(200,1); %label for the data
datalabel(1:100)=-1;
%train with Non-linear SVM classifier use Gaussian Kernel
model=svmtrain(datalabel,data,'-c 100 -g 4');
end該例中我們分別生成了100個正樣本和100個負樣本,如下圖所示,因為kernel type default=2(即Gaussian kernel),通過svmtrain(datalabel,data,'-c 100 -g 4')我們設定了第五節中獎的引數——C(c)和 2σ2(g)分別為100和4。
執行結果:
>> Nonlinear_SVM
*
optimization finished, #iter = 149
nu = 0.015538
obj = -155.369263, rho = 0.634344
nSV = 33, nBSV = 0
Total nSV = 33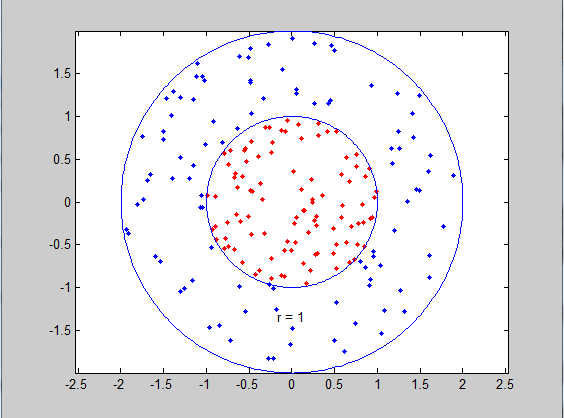
最後,我們比較一下logistic regresion和 SVM:
用n表示feature個數,m表示training exampl個數。
①當n>=m,如n=10000,m=10~1000時,建議用logistic regression, 或者linear kernel的SVM
②如果n小,m不大不小,如n=1~1000,m=10~10000,建議用Gaussian Kernel的SVM
③如果n很小,m很大,如n=1~1000,m>50000,建議增加更多的feature並使用logistic regression, 或者linear kernel的SVM
原因,①模型簡單即可解決,③如果還用Gaussian kernel會導致很慢,所以還選擇logistic regression或者linear kernel
神經網路可以解決以上任何問題,但是速度是一個很大的問題。
詳見下圖:

test:

我們可以把所有資料分為testset和training set兩部分進行訓練,example:
load heart_scale
[N D] = size(heart_scale_inst);
% Determine the train and test index,select top 200 as training data
% else as test data
trainIndex = zeros(N,1); trainIndex(1:200) = 1;
testIndex = zeros(N,1); testIndex(201:N) = 1;
trainData = heart_scale_inst(trainIndex==1,:);
trainLabel = heart_scale_label(trainIndex==1,:);
testData = heart_scale_inst(testIndex==1,:);
testLabel = heart_scale_label(testIndex==1,:);
% Train the SVM
model = svmtrain(trainLabel, trainData, '-c 1 -g 0.07 -b 1');
% Use the SVM model to classify the data
[predict_label, accuracy, prob_values] = svmpredict(testLabel, testData, model, '-b 1'); % run the SVM model on the test data執行結果:
optimization finished, #iter = 87
nu = 0.426369
obj = -56.026822, rho = -0.051128
nSV = 77, nBSV = 62
Total nSV = 77
*
optimization finished, #iter = 99
nu = 0.486493
obj = -64.811759, rho = 0.328505
nSV = 87, nBSV = 68
Total nSV = 87
*
optimization finished, #iter = 101
nu = 0.490332
obj = -64.930603, rho = 0.424679
nSV = 87, nBSV = 67
Total nSV = 87
*
optimization finished, #iter = 121
nu = 0.483649
obj = -64.046644, rho = 0.423762
nSV = 87, nBSV = 65
Total nSV = 87
*
optimization finished, #iter = 93
nu = 0.470980
obj = -63.270339, rho = 0.458209
nSV = 83, nBSV = 67
Total nSV = 83
*
optimization finished, #iter = 137
nu = 0.457422
obj = -76.730867, rho = 0.435233
nSV = 104, nBSV = 81
Total nSV = 104
Accuracy = 81.4286% (57/70) (classification)
>> 這裡只是一部分我做過的實驗,希望有朋友能夠有更完善的程式或者更好的資料推薦~謝謝!==============================================
小結
相關推薦
Stanford機器學習 第八講 支援向量機SVM
set type of SVM (default 0) 0 -- C-SVC 1 -- nu-SVC 2 -- one-class SVM 3 -- epsilon-SVR 4 -- nu-SVR-t kernel_type : set type of kernel functi
Stanford機器學習---第八講. 支援向量機SVM
本欄目(Machine learning)包括單引數的線性迴歸、多引數的線性迴歸、Octave Tutorial、Logistic Regression、Regularization、神經網路、機器學習系統設計、SVM(Support Vector Machines 支援向量
機器學習 第六章 支援向量機
6.1 間隔與支援向量 在樣本空間中,劃分超平面可通過如下線性方程來描述: 6.2 對偶問題 我們希望求解式(6.6)來得到大間隔劃分超平面所對應的模型: 對式(6.6)使用拉格朗日乘子法可得到其“對偶問
機器學習(三)——支援向量機SVM
SVM探討 目錄 SVM探討 SVM演算法 根據處理問題的複雜度,SVM 可由簡到繁分為三種: 線性可分支援向量機:硬間隔最大化。 線性支援向量機:資料分佈近似線性可分,可通過軟間隔最大化(懲罰因子,鬆弛變數)來線性分隔樣本點。 非線性支援向量機:通過核函式提升
Stanford機器學習---第七講 機器學習系統設計
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
Stanford機器學習---第九講 聚類
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
Andrew Ng 機器學習筆記 11 :支援向量機(Support Vector Machine)
構建支援向量機 1.替換邏輯迴歸函式 2.去除多餘的常數項 1/m 3.正則化項係數的處理 大間距分類器 SVM決
機器學習實戰筆記5—支援向量機
注:此係列文章裡的部分演算法和深度學習筆記系列裡的內容有重合的地方,深度學習筆記裡是看教學視訊做的筆記,此處文章是看《機器學習實戰》這本書所做的筆記,雖然演算法相同,但示例程式碼有所不同,多敲一遍沒有壞處,哈哈。(裡面用到的資料集、程式碼可以到網上搜索,很容易找到。)。Python版本3.6
機器學習與深度學習系列連載: 第一部分 機器學習(九)支援向量機2(Support Vector Machine)
另一種視角定義SVM:hinge Loss +kennel trick SVM 可以理解為就是hingle Loss和kernel 的組合 1. hinge Loss 還是讓我們回到二分類的問題,為了方便起見,我們y=1 看做是一類,y=-1 看做是另一類
【機器學習筆記17】支援向量機
【參考資料】 【1】《統計學習方法》 基本概念 當訓練資料線性可分時,通過硬間隔最大化,學習一個線性的分類器,即線性可分支援向量機,又稱硬間隔支援向量機; 當訓練資料近似線性可分時,通過軟間隔(增加一個鬆弛因子)後學習一個線性的分類器,即軟間隔支援向量機;
機器學習之旅:支援向量機通俗導論(理解SVM的三層境界)
支援向量機通俗導論(理解SVM的三層境界)作者:July、pluskid ;致謝:白石、JerryLead出處:結構之法演算法之道blog。前言 動筆寫這個支援向量機(support vector machine)是費了不少勁和困難的,原因很簡單,一者這個東西本身就並
自學機器學習之sklearn實現支援向量機
對於支援向量機,我看了好久也沒能看的很明白,裡面的理論有點多。所以呢,只能用sklearn來跑跑svm模型了。。 下面是程式碼:(svm支援多類別分類,所以這次還使用iris的資料) from sklearn import svm from skle
【機器學習演算法推導】支援向量機
線性可分 在二維平面中,正樣本和負樣本可以由一條直線完全隔開。假設存在直線 y =
【機器學習實戰-python3】支援向量機(Support Vecrtor Machines SVM)
工具:PythonCharm 書中的程式碼是python2的,而我用的python3,結合實踐過程,這裡會標註實踐時遇到的問題和針對python3的修改。 實踐程式碼和訓練測試資料可以參考這裡 https://github.com/stonycat/ML
機器學習筆記09:支援向量機(二)-核函式(Kernels)
核函式是 SVM 的最重要的部分,我們可以通過設定不同的核函式來創造出非常複雜的、非線性的支援向量機。 1.核(Kernel) 首先來看看什麼是核函式。如圖所示,假設有一個樣本 x 有兩個特徵 x1,x2,我們可以根據與地標(landmarks) l(1),
機器學習(7)——支援向量機(二):線性可分支援向量機到非線性支援向量機
線性可分支援向量機 回顧 前面總結了線性可分支援向量機,知道了支援向量機的最終目的就是通過“間隔最大化” 得到最優分類器,能夠使最難區分的樣本點得到最大的分類確信度,而這些難區分的樣本就是支援向量。 還是如下圖所示,超平面H1 和 H2 支撐著中間的決
《機器學習_07_01_svm_硬間隔支援向量機與SMO》
### 一.簡介 支援向量機(svm)的想法與前面介紹的感知機模型類似,找一個超平面將正負樣本分開,但svm的想法要更深入了一步,它要求正負樣本中離超平面最近的點的距離要儘可能的大,所以svm模型建模可以分為兩個子問題: (1)分的對:怎麼能讓超平面將正負樣本分的開; (2)分的好:怎麼能讓距離超平
《機器學習_07_02_svm_軟間隔支援向量機》
### 一.簡介 上一節介紹了硬間隔支援向量機,它可以在嚴格線性可分的資料集上工作的很好,但對於非嚴格線性可分的情況往往就表現很差了,比如: ```python import numpy as np import matplotlib.pyplot as plt import copy import ra
機器學習(十一) 支持向量機 SVM(上)
gin 模型 結構 線性可分 adding 統計學習 lis 可能 方法 一、什麽是支撐向量機SVM (Support Vector Machine) SVM(Support Vector Machine)指的是支持向量機,是常見的一種判別方法。在機器學習領域,是一個有監
【深度學習基礎-06】支援向量機SVM(下)-線性不可分
1 SVM的優點
