6 MATLAB引數估計與假設-正態總體引數的檢驗
正態總體引數的檢驗
更多MATLAB資料分析視訊請點選,或者在網易雲課堂上搜索《MATLAB資料分析與統計》 http://study.163.com/course/courseMain.htm?courseId=1003615016
1 總體標準差已知時的單個正態總體均值的U檢驗
例:
某切割機正常工作時,切割的金屬棒的長度服從正態分佈N(100,4)。從該切割機切割的一批金屬棒中隨機抽取15根,測得長度為:
97 102 105 112 99 103 102 94 100 95 105 98 102 100 103
假設總體的方差不變,試檢驗該切割機工作是否正常,即檢驗總體均值是否等於100?,取顯著性水平a=0.05。
分析:
這是總體標準差已知時的單個正態總體均值的檢驗,根據題目要求可寫出如下假設:
H0:u=u0=100, H1=u /=u0(u不等於u0)
H0稱為原假設,H1稱為被擇假設(或對立假設)
MATLAB統計工具箱中的ztest函式用來做總體標準差已知時的單個正態總體均值的檢驗
呼叫格式ztest
[h,p,muci,zval]=ztest(x,mu0,Sigma,Alpha,Tail)
x:是輸入的觀測向量
mu0:假設的均值
Sigma:總體標準差
Alpha:顯著性水平,預設0.05
Tail:尾部型別變數,‘both’雙側檢驗(預設),u不等於uo;‘right’右側檢驗,u>u0; ‘left’左側檢驗,u<u0;
返回值:
h:假設的結果(0,1),h=0時,接受假設H0;h=1,拒絕假設H0
p:檢驗的p值,p>Alpha時,接受原假設H0;p<=Alpha時,拒絕原假設H0.
muci:總體均值u的置信水平為1-Alpha的置信區間
zval:檢驗統計量的觀測值
%定義樣本觀測值向量
x=[97 102 105 112 99 103 102 94 100 95 105 98 102 100 103];
mu0=100; %原假設中的mu0
sigma=2; %總體標準差
Alpha=0.05; %顯著性水平
%呼叫ztest函式做總體均值的雙側檢驗(預設),
%返回變數h,檢驗的p值,均值的置信區間muci,檢驗統計量的觀測值zval
[h,p,muci,zval]=ztest(x,mu0,sigma,Alpha)
h =
1
p =
0.0282
muci =
100.1212 102.1455
zval =
2.1947
由ztest函式返回值可以看到,h=1,且p=0.0282<0.05,所以在顯著性水平=0.05下拒絕的原假設H0:u=u0=100,因此認為該切割機不能正常工作,同時還返回了總體均值的置信水平為95%(1-0.05)的置信區間為[100.1212 102.1455]。
現在我們已經知道u不等於u0(100),那麼接下來還需要做如下的檢驗
H0:u<=u0=100; H1:u>u0
這裡就需要設定一下尾部型別變量了,Tail用來指定備擇假設H1的形式,它可能取的字串‘both’,‘right’和'left',對應的備擇假設分別為H1:u/=u0(不等於),(雙側檢驗)、
H1:u>u0,(右尾檢驗)和H1:u<u0(左尾檢驗)
%定義樣本觀測值向量
x=[97 102 105 112 99 103 102 94 100 95 105 98 102 100 103];
mu0=100; %原假設中的mu0
sigma=2; %總體標準差
Alpha=0.05; %顯著性水平
tail='right';
%呼叫ztest函式做總體均值的雙側檢驗(預設),
%返回變數h,檢驗的p值,均值的置信區間muci,檢驗統計量的觀測值zval
[h,p,muci,zval]=ztest(x,mu0,sigma,Alpha,tail)
h =
1
p =
0.0141
muci =
100.2839 Inf
zval =
2.1947
返回值中,h=1且p=0.0141<0.05,在顯著性水平下=0.05下拒絕了原假設H0:u<=u0=100;
如果:
H0:u>uo=100; H1=u<u0
那麼tail應為‘left’;
返回值將會 h=0,p>0.05,接受原假設H0,即認為u>100;
2 總體標準差未知時的單個正態總體均值的t檢驗
例:
化肥廠用自動包裝機包裝化肥,某日測得9包化肥的質量如下:
49.4 50.5 50.7 51.7 49.8 47.9 49.2 51.4 48.9
設每包化肥的質量服從正態分佈,是否可以認為每包化肥的平均質量為50?取顯著性水平a=0.05。
分析:這是總體標準差未知時的單個正態總體均值的檢驗,根據題目要求可以寫出如下假設:
H0:u=u0=50, H1:u/=u0(u不等於u0)
MATLAB統計工具箱中提供了ttest函式用來做總體標準差未知時的正態總體均值的檢驗,呼叫格式和ztest類似,返回值有點不同
[h,p,muci,stats]=ttest(x,mu0,Alpha,Tail)
輸入引數中沒有標準差,其它都一樣
返回值stats是一個結構體變數,包括t檢驗統計量的觀測值,自由度,和樣本的標準差;其它都一樣
%定義樣本觀測值向量
x=[49.9 50.5 50.7 51.7 49.8 47.9 49.2 51.4 48.9];
mu0=50; %原假設中的均值u0=50
Alpha=0.05; %顯著性水平alpha
%呼叫ttest函式做總體均值的雙側檢驗
%返回變數h,檢驗值p,均值的置信空間muci,結構體變數stats
[h,p,muci,stats]=ttest(x,mu0,Alpha)
h =
0
p =
1.0000
muci =
49.0625 50.9375
stats =
tstat: -1.7478e-14
df: 8
sd: 1.2196
由於返回值h=0,p=1>0.05,所以在顯著性水平=0.05下接受原假設H0:u=u0=50,認為每包化肥的平均質量為50,並且總體均值u的置信水平為95%的置信區間為[49.0625 50.9375]
3 總體標準差未知時的兩個正態總體均值的比較 t 檢驗
(1)兩獨立樣本的 t 檢驗
例:
甲、乙兩臺機床加工同一種產品,從這兩臺機床加工的產品中隨機抽取若干件,測得產品直徑為:
甲機床:20.1,20.0,19.3,20.6,20.2,19.9,20.0,19.9,19.1,19.9
乙機床:18.6, 19.1,20.0,20.0,20.0,19.7,19.9,19.6,20.2
設甲、乙兩機床加工的產品的直徑分佈服從正態分佈N(u1,a1^2)和N(u2,a2^2),試比較甲、乙兩臺機床加工的產品的直徑均值是否有顯著性差異,取顯著性水平a=0.05
分析:這是總體標準差未知,並且兩樣本是相互獨立的,對這兩樣本均值做比較檢驗,根據題目要求,可寫出如下假設
H0:u1=u2 H1:u1/=u2(u1不等於u2)
MATLAB統計工具箱中的ttest2函式可以用來做總體標準差未知時的兩個正態總體均值的比較檢驗;
呼叫格式:
[h,p,muci,stats]=ttest(x,y,Alpha,Tail,vartype)
x,y為輸入的兩個樣本觀測值
Alpha為顯著性水平
tail為尾部型別
cartype:為方差型別,用來指定兩總體方差是否相等,‘equal’表示等方差,‘unequal’表示異方差
返回值與ttest函式一致,muci是指均值差的置信空間
%定義甲機床的樣本觀測值向量
x=[20.1,20.0,19.3,20.6,20.2,19.9,20.0,19.9,19.1,19.9];
%定義乙機床的樣本觀測值向量
y=[18.6, 19.1,20.0,20.0,20.0,19.7,19.9,19.6,20.2];
Alpha=0.05; %顯著性水平
tail='both'; %尾部型別為雙側
vartype='equal'; %方差型別為等方差
%呼叫ttest2函式作兩個正態總體均值的比較檢驗
%返回變數h,檢驗的p值,均值差的置信區間,結構體變數stats
[h,p,muci,stats]=ttest2(x,y,Alpha,tail,vartype)
h =
0
p =
0.3191
muci =
-0.2346 0.6791
stats =
tstat: 1.0263
df: 17
sd: 0.4713
返回的檢驗值p>0.05,所以在顯著性水平=0.05下,接受原假設H0:u1=u2,認為甲、乙兩臺機床加工的產品的直徑沒有顯著差異。此時,u1-u2的置信水平為95%的置信區間為[-0.2346 0.6791]
(2)配對樣本的 t 檢驗
(兩樣本不是獨立的)
例:
兩組(各10名)有資質的評酒員分別對12種不同的酒進行品評,每個評酒員在品嚐後進行評分,然後對每組的每個樣品計算其平均分,評分結果如下
樣品1 樣本2 樣品3 樣品4 樣品5 樣品6 樣品7 樣品8 樣品9 樣品10 樣品11 樣品12
第一組 80.3 68.6 72.2 71.5 72.3 70.1 74.6 73.0 58.7 78.6 85.6 78.0
第二組 74.0 71.2 66.3 65.3 66.0 61.6 68.8 72.6 65.7 72.6 77.1 71.5
設兩組評酒員的評分分佈服從正態分佈N(u1,a1^2)和N(u2,a2^2),試比較兩組評酒員的評分是否有顯著差異,取顯著性水平a=0.05
分析:由於每個紅酒樣本都對應兩個評分,顯然樣本等長,並且兩樣本不獨立,這是配對樣本的比較問題,根據題目要求可寫出如下的假設:
H0:u1=u2, H1:u1/=u2(u1不等於u2)
由於兩個樣本不獨立,通常的做法是將兩個樣本對應資料最差,把兩個正態總體均值的比較檢驗轉化為單個正態總體均值的檢驗,然後就可用ttest函式進行檢驗
上面的假設改寫為如下假設
H0:u=u1-u2=0, H1:u/=0(u不等於0)
然後呼叫ttest函作配對樣本的比較 t 檢驗
呼叫格式
[h,p,muci,stats]=ttest(x,y,Alpha,Tail)
x,y為輸入的觀測樣本觀測值向量,其它引數與ttest一致
%樣本1
x=[80.3,68.6,72.2,71.5,72.3,70.1,74.6,73.0,58.7,78.6,85.6,78.0];
%樣本2
y=[74.0,71.2,66.3,65.3,66.0,61.6,68.8,72.6,65.7,72.6,77.1,71.5];
Alpha=0.05; %顯著性水平
tail='both'; %尾部型別為雙側
%呼叫ttest函式作配對樣本的比較t檢驗
%返回變數h,檢驗的p值,均值差的置信區間muci,結構體變數stats
[h,p,muci,stats]=ttest(x,y,Alpha,tail)
h =
1
p =
0.0105
muci =
1.2050 7.2617
stats =
tstat: 3.0768
df: 11
sd: 4.7662
返回值p=0.0105<0.05,所以在顯著性水平a=0.05下拒絕原假設H0:u=u1-u2=0,認為兩組評酒員的評分有顯著差異。此時兩總體均值差的置信水平為95%的置信區間為
[ 1.2050 7.2617],該區間不包含0,說明第一組評酒員的評分明顯高於第二組評酒員的評分。
4 總體均值未知時的單個正態總體方差的卡方檢驗
例:
化肥廠用自動包裝機包裝化肥,某日測得9包化肥的質量如下:
49.4 50.5 50.7 51.7 49.8 47.9 49.2 51.4 48.9
設每包化肥的質量服從正態分佈,是否可以認為每包化肥的質量的方差等於1.5?取顯著性水平a=0.05。
分析:這是總體均值未知時的單個正態總體方差的檢驗,根據題目要求可以寫出如下假設:
H0:a^2=a0^2=1.5, H1:a^2/=a0^2(a^2不等於a0^2)
MATLAB統計工具箱中的vartest函式可用來做總體均值未知時的單個正態總體方差的檢驗
呼叫格式:
[h,p,varci,stats]=vattest(x,v,alpha,tail)
輸出引數
x:樣本觀測值向量
v:原假設中的方差
alpha:顯著性水平
tail:尾部型別
輸出引數
varci為方差的置信區間,其他都一樣
%定義樣本觀測值向量
x=[49.9,50.5,50.7,51.7,49.8,47.9,49.2,51.4,48.9];
var0=1.5; %原假設中的方差
Alpha=0.05; %顯著性水平
tail='both'; %尾部型別為雙側
%呼叫vartest函式作單個正態總體方差的雙側檢驗
%返回值變數h,檢驗值p,方差的置信區間varci,結構體變數stats
[h,p,varci,stats]=vartest(x,var0,Alpha,tail)
h =
0
p =
0.8800
varci =
0.6787 5.4594
stats =
chisqstat: 7.9333 %卡方檢驗統計量的觀測值
df: 8 %卡方檢驗統計量的自由度
返回值p=0.88>0.05,所以在顯著性水平a=0.05下接受原假設H0:a^2=a0^2=1.5,認為每包化肥的質量的方差等於1.5,此時總體方差a^2的置信水平為95%的置信區間為[0.6787 5.4594]
5 總體均值未知時的兩個正態總體方差的比較F檢驗
甲、乙兩臺機床加工同一種產品,從這兩臺機床加工的產品中隨機抽取若干件,測得產品直徑為:
甲機床:20.1,20.0,19.3,20.6,20.2,19.9,20.0,19.9,19.1,19.9
乙機床:18.6, 19.1,20.0,20.0,20.0,19.7,19.9,19.6,20.2
設甲、乙兩機床加工的產品的直徑分佈服從正態分佈N(u1,a1^2)和N(u2,a2^2),試比較甲、乙兩臺機床加工的產品的直徑方差是否有顯著性差異,取顯著性水平a=0.05
分析:這是總體均值未知時的兩個正態總體方差的比較檢驗,根據題目要求可寫出如下假設:
H0:a1^2=a2^2, H1:a1^2/=a2^2(a1^2不等於a2^2)
MATLAB統計工具箱中的vartest2函式可以用來做總體均值未知時的兩個正態總體方差的比較檢驗
呼叫格式:
[h,p,varci,stats]=vattest2(x,y,alpha,tail)
輸入引數:
x,y為樣本觀測值向量
alpha:顯著性水平
tail:尾部型別
返回值與vartest函式一致,置信區間varci是a1^2/a2^2的置信區間
%定義甲機床的樣本觀測值向量
x=[20.1,20.0,19.3,20.6,20.2,19.9,20.0,19.9,19.1,19.9];
%定義乙機床的樣本觀測值向量
y=[18.6, 19.1,20.0,20.0,20.0,19.7,19.9,19.6,20.2];
Alpha=0.05; %顯著性水平
tail='both'; %尾部型別為雙側
[h,p,varci,stats]=vartest2(x,y,Alpha,tail)
h =
0
p =
0.5798
varci =
0.1567 2.8001
stats =
fstat: 0.6826 %F檢驗統計量的觀測值
df1: 9 %F檢驗統計量的分子自由度
df2: 8 %F檢驗統計量的分母自由度
返回的檢驗的p值p=0.5789>0.05,所以在顯著性水平a=0.05下接受原假設H0:a1^2=a2^2,認為甲乙兩臺機床加工產品的直徑的方差相等。此時a1^2/a2^2的置信水平為95%的置信區間為[ 0.1567 2.8001]
6 檢驗功效與樣本容量的計算
(1)假設檢驗的兩類錯誤
假設檢驗可能會犯兩類錯誤:第一類錯誤是本來原假設H0正確,卻由於抽樣的原因拒絕了H0,這類錯誤又稱之為“拒真”錯誤,犯第一類錯誤的概率記為a;第二類錯誤是本來H0不正確,卻由於抽樣的原因接受了H0,這類錯誤又稱為“取偽”錯誤,犯第二類錯誤的概率記為b,假設檢驗需要控制犯兩類錯誤的概率均在一個較低的水平,而實際上在樣本容量固定的前提下,降低a的同時會增加b,,降低b的同時a也會增加,為了平衡這一矛盾,提出了顯著性檢驗的概念,也就是在控制犯第一類錯誤的概率不超過某一水平(即顯著性水平)的前提下去制約b。
(2)檢驗功效與樣本容量的關係
原假設不成立的條件下,拒絕原假設的概率(即1-b)稱為檢驗的功效,它反映了一個顯著性檢驗能夠區分原假設和備擇假設的能力,通常情況下,應使得檢驗功效達到一個較高的水平(例如90%以上)。
當給定樣本容量時可以求得檢驗功效,樣本容量越大,檢驗功效越高,即區分原假設與備擇假設的能力越強;反之,給定檢驗功效,也可求出樣本容量
(3) 呼叫sampsizepwr函式求樣本容量和檢驗功效
MATLAB統計工具箱中提供了sampsizepwr函式,用來求樣本容量和檢驗功效,其呼叫格式如下:
<1> n=sampsizepwr(testtype,p0,p1)
對於不同型別的雙側檢驗,在顯著性水平0.05下,求使得檢驗功效不低於90%的最小的樣本容量n。輸入引數p0和p1分別用來指定原假設和備擇假設中的引數值,testtype用來指定檢驗型別,是字串變數,其取值如下表
testtype引數取值 說明 備註
‘z’ 標準差已知時 p0是形如[u0,a0]的向量,其元素分別為原假設對應的總體均值
正態總體均值的檢驗 和標準差。p1是備擇假設對應的總體均值
‘t’ 標準差未知正態總體 p0是形如[u0,a0]的向量,其元素分別為原假設對應的總體均值
均值的檢驗 和樣本標準差,p1是備擇假設對應的總體均值
‘var’ 正態總體的方差檢驗 p0和p1分別是原假設和備擇假設對應的總體方差
‘p’ 二項分佈的比例(成功概率)檢驗 p0和p1分別是原假設和備擇假設對應的引數值
當引數p1為向量時,輸出引數n是與p1等長的向量
<2>n=sampsizepwr(testtype,p0,p1,power)
求樣本容量,用power引數指定引數功效,其值介於0-1之間
<3>power=sampsizepwr(testtype,p0,p1,[ ],n)
給定樣本容量n,求檢驗功效power
<4>p1=sampsizepwr(testtype,p0,[ ],power,n)
給定樣本容量n和檢驗功效power,求備擇假設中的引數p1.
<5> [......]=sampsizepwr(.....,n,param1,val1,param2,val2,......)
用可選的成對出現的引數名和引數值控制計算結果,可用的引數名與引數值如下
引數名 引數值及說明
‘alpha’ 檢驗的顯著性水平,取值0--1之間,預設值0.05
‘tail’ 尾部型別變數,用來指定備擇假設的形式,
可取值‘both’,‘right’,‘left’
例:設需要對某一正態總體的均值進行如下檢驗:
H0:u=100, H1:u>104
已知總體標準差a=6.58,取顯著性水平=0.05,同時要求檢驗功效達到90%以上,求所需要的樣本容量
呼叫sampsizepwr函式求解
mu0=100; %原假設對應的總體均值
sigma0=6.58; %原假設對應的標準差
mu1=104; %備擇假設對應的總體均值
pow=0.9; %檢驗功效
%呼叫sampsizepwr函式求樣本容量
n=sampsizepwr('z',[mu0,sigma0],mu1,pow,[],'tail','right')
n =
24
要檢驗功效達到90%以上,需要的樣本容量至少為24,如果指定不同的樣本容量,還可求得相應的檢驗功效
n=1:60; %指定不同的樣本容量,1,2,....60
mu0=100; %原假設對應的總體均值
sigma0=6.58; %原假設對應的標準差
mu1=104; %備擇假設對應的總體均值
%呼叫sampsizepwr函式求不同樣本容量對應的檢驗功效
pow=sampsizepwr('z',[mu0,sigma0],mu1,[],n,'tail','right');
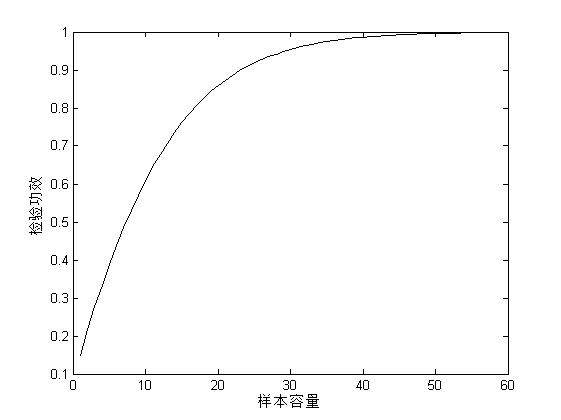
plot(n,pow,'k'); %繪製檢驗功效與樣本容量關係曲線
xlabel('樣本容量');
ylabel('檢驗功效');
由圖可知,隨著樣本容量的增大, 檢驗功效逐漸趨向於1.
更多MATLAB資料分析視訊請點選,或者在網易雲課堂上搜索《MATLAB資料分析與統計》 http://study.163.com/course/courseMain.htm?courseId=1003615016