關於遞迴，必須瞭解其關鍵的思想，重複相同的動作，但處理的卻是不同的資料，在幾乎所有我所見過的遞迴函式中，都是這樣. 幾乎都是讓資料之間進行交換，然後以相同的“機器”去加工.
故此引入著名的Tower of Hanoi：

#include<stdio.h>
void hanoi(int n, char A, char B, char C)
{

    if (n == 1)
    {
        printf("Move disk %d from %c to %c\n", n, A, C);
    }
    else
    {
        hanoi(n - 1
 
, A, C, B);
        printf("Move disk %d from %c to %c\n", n, A, C);
        hanoi(n - 1, B, A, C);
    }
}

void main()
{
    int n;
    printf("請輸入數字n以解決n階漢諾塔問題：\n");
    scanf("%d", &n);
    hanoi(n, 'A', 'B', 'C');
    fflush(stdin);
    getchar();
}

觀察程式碼，
第一個遞迴語句，交換後兩個目標（塔）
第二個遞迴語句，交換前兩個目標（塔）

通過一步步的執行，我們也同樣會發現，第一個遞迴語句呼叫並返回初始時，正是把n-1個（最大的盤子的上邊所有的）盤子移到了別的柱子上.
此時，我們就要從漢諾塔的具體情況來分析了，其所要做的，就是把n-1通過B移到C（當然可以c到b），然後把第n移到B，然後把之前的n個通過A移到B，而其遞迴的插入點，就是從0到n的移動，記住，當移動上面的任何多少層塔時，其下面的任何多少層塔都是可以無視的，總比其上打，且其上的任何多少層塔的移動，都是靠一個柱子移到另一個柱子.


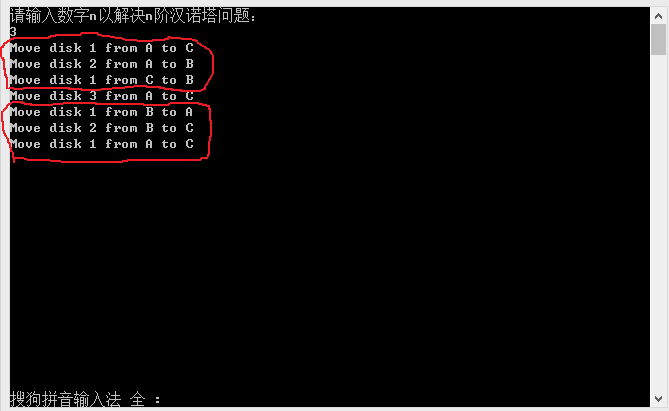
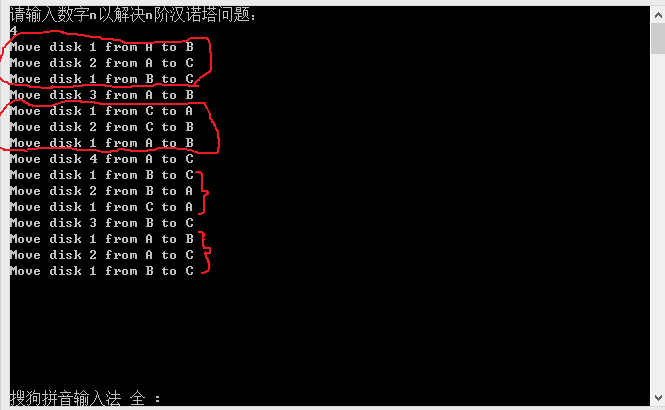
 其實，總的來說，遞迴演算法可以說是從結果出發的，以發現其規律性.