機器學習之Bagging 與 隨機森林演算法
在整合學習裡面,有兩種流派,一個是 boosting 流派,它的特點是對於各個學習器之間有著相互依賴的關係 (比如說在某一次演算法結束後,分類錯誤的樣本會增大比例,以引起下一次的訓練時候的關注度),另一種是bagging 流派,它的特點是各個學習器之間沒有任何的依賴關係,可以並行擬合。
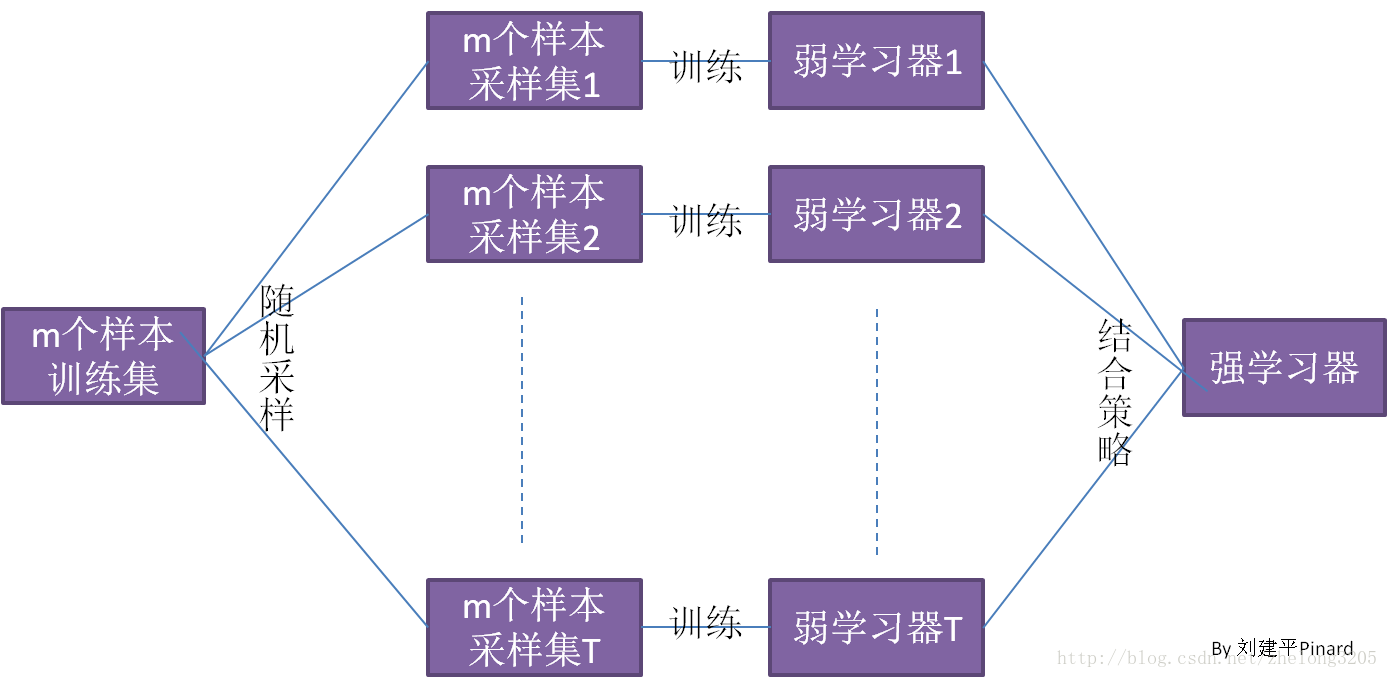
Bagging 原理
從圖中,我們可以看出, bagging 學習演算法 沒有 adaboost 演算法那樣的聯絡,它的關鍵之處在於“隨機取樣“。
什麼是隨機取樣呢 ?
就是我們固定從訓練集中採集固定個數的樣本,但是這種採集是一種有放回的採集,對於每一次採集,我們都將這一次採集到的樣本放回,也就是說我們可能採集到重複的樣本,對於這個演算法我們一般會隨機採集與樣本訓練樣本數目相同的樣本,這樣得到的取樣集和訓練集合樣本數目相同,但是內容不同,對於資料集m個樣本的進行T次隨機取樣,得到訓練T個訓練器的訓練集。 注意 (Bagging 是有放回隨機取樣)
有概率論知識可以得到,每一次取樣每一個樣本被採集到的概率為 1 / m,不被採集到的概率為 1 - 1 / m 則 m 次都沒有被採集到的概率為 1/e = 36.8。我們稱之為袋外資料用來當做測試集,來檢驗模型的泛化能力。
與 Adaboost 演算法一樣 一般Bagging演算法的基礎學習器是神經網路或者決策樹。
對於這個演算法如果是預測離散值則採用投票法,對於連續值則採用求平均的方法。
Bagging 演算法流程
相對於Boosting系列的Adaboost和GBDT,bagging演算法要簡單的多。
- 輸入資料集
- 輸入迭代次數 T
- 隨機取樣 T 次 每次取 m 個樣本
- 對於每一次樣本訓練一個基礎學習器
- 得到最終學習器
隨機森林演算法 (RF)
隨機森林演算法是一種改進版的 bagging 演算法,首先隨機森林使用決策樹(一般是 CART,也有C4.5)當做基學習器。在決策樹的基礎上隨機森林對決策樹的建立經行了改進。
它的改進之處在於 :
對於一般的決策樹而言,我們會在它所有n個樣本特徵中選擇一個最優化特徵來作為這個節點的特徵劃分,但是隨機森林是通過隨機選擇節點上的一些特徵,這個數字小於n,假設為 n sub,然後在這些隨機選擇的 n 個樣本特徵中,選擇一個最優特徵作為決策樹的劃分,(這便是隨機森林的隨機之處)這樣進一步增加了模型的泛化能力,減小了過擬合的風險
在實際的操作中,如果 nsub 過於小則會導致訓練效果不好,偏差較大,如果nsub 太大的話則可能產生過擬合的風險,所以一般我們採用交叉驗證的方法確定一個合適的nsub。