轉載連結

一、前向星

1、

我們首先來看一下什麼是前向星.

前向星是一種特殊的 邊集 陣列 ,我們把邊集陣列中的每一條邊按照起點從小到大排序,  如果起點相同就按照終點從小到大排序,

並記錄下以某個點為起點的所有邊在陣列中的起始位置和儲存長度,那麼前向星就構造好了.

用 len[i]     來記錄所有以i為起點的邊的個數

用 head[i]  記錄以i為邊集在陣列中的第一個儲存位置.

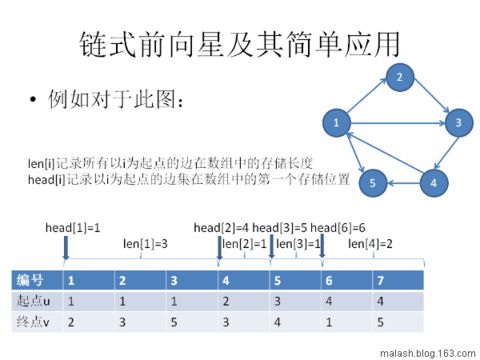
我們輸入邊的順序為:

1 2

2 3

3 4

1 3

4 1

1 5

4 5

那麼排完序後就得到:

編號:     1      2      3      4      5      6      7

起點u:    1      1      1      2      3      4      4

終點v:    2      3      5      3      4      1      5

得到:

head[1] = 1    len[1] = 3

head[2] = 4    len[2] = 1

head[3] = 5    len[3] = 1

head[4] = 6    len[4] = 2

2、前向星的 CODE

構建邊的結構

struct NODE
{
    int from;      //起點  
    int to;        //終點  
    bool operator < (const NODE & a) const
    {
        return (from == a.from&&to<a.to) || from<a.from;
    }
};
 

 初始化：

void Init()
{
    for (int i = 0; i<m; ++i)            //讀入資料  
        cin >> edge[i].from >> edge[i].to;
    sort(edge, edge + m);              //排序  
    memset(head, -1, sizeof(head));
    head[edge[0].from] = 0;
    for (int i = 1; i<m; ++i)
        if (edge[i].from != edge[i - 1].from) head[edge[i].from] = i;
}
 

對圖的遍歷：

void solve()      //遍歷整個圖  
{
    for (int i = 0; i < n; ++i)
    {
        for (int k = head[i]; edge[k].from == i&&k<m; ++k)
        {
            cout << edge[k].from << " " << edge[k].to << endl;
        }
    }
}

3、

利用前向星，我們用 O(1) 的時間找到 以 i 為起點的第一條邊 ，以 O(len[ i]) 的時間找到以 i 為起點的所有邊

前向星適合用來優化稀疏圖的深度優先搜尋、廣搜、單源最短路徑（SPFA)

但對所有邊按起點排序，以快排計算，至少需要  O(nlog(n)) 的複雜度

所有就引出   鏈式前向星

二、鏈式前向星

如果用鏈式前向星,就可以避免排序.

前向性的構造主要耗時在頻繁的交換，如果將連結串列也引入前向星，則不用快排就可以實現同樣的效果

我們建立邊結構體為:

struct Edge

{

     int next;

     int to;

     int w;

};

其中   edge[i].to——表示第 i 條邊的終點,

          edge[i].next ——表示與第 i 條邊同起點的下一條邊的儲存位置,

          edge[i].w——邊權值.

          head[]——用來表示以i為起點的第一條邊儲存的位置,實際上你會發現這裡的第一條邊儲存的位置其實

          在以i為起點的所有邊的最後輸入的那個編號.

           head[]陣列一般初始化為-1,對於加邊的add函式是這樣的:

void add(int u,int v,int w)  
{    
    edge[cnt].to = v;  
    edge[cnt].next = head[u];
    edge[cnt].w = w;  
    head[u] = cnt++;  
}  

初始化cnt = 0,這樣,現在我們還是按照上面的圖和輸入來模擬一下:

edge[0].to = 2;     edge[0].next = -1;      head[1] = 0;

edge[1].to = 3;     edge[1].next = -1;      head[2] = 1;

edge[2].to = 4;     edge[2],next = -1;      head[3] = 2;

edge[3].to = 3;     edge[3].next = 0;       head[1] = 3;

edge[4].to = 1;     edge[4].next = -1;      head[4] = 4;

edge[5].to = 5;     edge[5].next = 3;       head[1] = 5;

edge[6].to = 5;     edge[6].next = 4;       head[4] = 6;

很明顯,head[i]儲存的是以i為起點的所有邊中編號最大的那個,而把這個當作頂點i的第一條起始邊的位置.

這樣在遍歷時是倒著遍歷的,也就是說與輸入順序是相反的,不過這樣不影響結果的正確性.

比如以上圖為例,以節點1為起點的邊有3條,它們的編號分別是0,3,5   而head[1] = 5

我們在遍歷以u節點為起始位置的所有邊的時候是這樣的:

for(int i=head[u];~i;i=edge[i].next)
 // 當 i等於 -1 的時候停止， -1 取反為 0

那麼就是說先遍歷編號為5的邊,也就是head[1],然後就是edge[5].next,也就是編號3的邊,然後繼續edge[3].next,也

就是編號0的邊,可以看出是逆序的.