工程實踐中，多數情況下，大矩陣一般都為稀疏矩陣，所以如何處理稀疏矩陣在實際中就非常重要。本文以python裡中的實現為例，首先來探討一下稀疏矩陣是如何儲存表示的。

1.sparse模組初探

python中scipy模組中，有一個模組叫sparse模組，就是專門為了解決稀疏矩陣而生。本文的大部分內容，其實就是基於sparse模組而來的。
第一步自然就是匯入sparse模組

>>> from scipy import sparse

然後help一把，先來看個大概

>>> help(sparse)

直接找到我們最關心的部分：

    Usage information
    =================

    There are seven
 
 available sparse matrix types:

        1. csc_matrix: Compressed Sparse Column format
        2. csr_matrix: Compressed Sparse Row format
        3. bsr_matrix: Block Sparse Row format
        4. lil_matrix: List of Lists format
        5. dok_matrix: Dictionary of Keys format
        6. coo_matrix: COOrdinate format
 
 (aka IJV, triplet format)
        7. dia_matrix: DIAgonal format

    To construct a matrix efficiently, use either dok_matrix or lil_matrix.
    The lil_matrix class supports basic slicing and fancy
    indexing with a similar syntax to NumPy arrays.  As illustrated below,
    the COO format may also be used to
 
 efficiently construct matrices.

    To perform manipulations such as multiplication or inversion, first
    convert the matrix to either CSC or CSR format. The lil_matrix format is
    row-based, so conversion to CSR is efficient, whereas conversion to CSC
    is less so.

    All conversions among the CSR, CSC, and COO formats are efficient,
    linear-time operations.

通過這段描述，我們對sparse模組就有了個大致的瞭解。sparse模組裡面有7種儲存稀疏矩陣的方式。接下來，我們對這7種方式來做個一一介紹。

2.coo_matrix

coo_matrix是最簡單的儲存方式。採用三個陣列row、col和data儲存非零元素的資訊。這三個陣列的長度相同，row儲存元素的行，col儲存元素的列，data儲存元素的值。一般來說，coo_matrix主要用來建立矩陣，因為coo_matrix無法對矩陣的元素進行增刪改等操作，一旦矩陣建立成功以後，會轉化為其他形式的矩陣。

>>> row = [2,2,3,2]
>>> col = [3,4,2,3]
>>> c = sparse.coo_matrix((data,(row,col)),shape=(5,6))
>>> print c.toarray()
[[0 0 0 0 0 0]
 [0 0 0 0 0 0]
 [0 0 0 5 2 0]
 [0 0 3 0 0 0]
 [0 0 0 0 0 0]]

稍微需要注意的一點是，用coo_matrix建立矩陣的時候，相同的行列座標可以出現多次。矩陣被真正建立完成以後，相應的座標值會加起來得到最終的結果。

3.dok_matrix與lil_matrix

dok_matrix和lil_matrix適用的場景是逐漸新增矩陣的元素。doc_matrix的策略是採用字典來記錄矩陣中不為0的元素。自然，字典的key存的是記錄元素的位置資訊的元祖，value是記錄元素的具體值。

>>> import numpy as np
>>> from scipy.sparse import dok_matrix
>>> S = dok_matrix((5, 5), dtype=np.float32)
>>> for i in range(5):
...     for j in range(5):
...             S[i, j] = i + j
...
>>> print S.toarray()
[[ 0.  1.  2.  3.  4.]
 [ 1.  2.  3.  4.  5.]
 [ 2.  3.  4.  5.  6.]
 [ 3.  4.  5.  6.  7.]
 [ 4.  5.  6.  7.  8.]]

lil_matrix則是使用兩個列表儲存非0元素。data儲存每行中的非零元素,rows儲存非零元素所在的列。這種格式也很適合逐個新增元素，並且能快速獲取行相關的資料。

>>> from scipy.sparse import lil_matrix
>>> l = lil_matrix((6,5))
>>> l[2,3] = 1
>>> l[3,4] = 2
>>> l[3,2] = 3
>>> print l.toarray()
[[ 0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.]
 [ 0.  0.  0.  1.  0.]
 [ 0.  0.  3.  0.  2.]
 [ 0.  0.  0.  0.  0.]
 [ 0.  0.  0.  0.  0.]]
>>> print l.data
[[] [] [1.0] [3.0, 2.0] [] []]
>>> print l.rows
[[] [] [3] [2, 4] [] []]

由上面的分析很容易可以看出，上面兩種構建稀疏矩陣的方式，一般也是用來通過逐漸新增非零元素的方式來構建矩陣，然後轉換成其他可以快速計算的矩陣儲存方式。

4.dia_matrix

這是一種對角線的儲存方式。其中，列代表對角線，行代表行。如果對角線上的元素全為0，則省略。
如果原始矩陣是個對角性很好的矩陣那壓縮率會非常高。
找了網路上的一張圖，大家就很容易能看明白其中的原理。

5.csr_matrix與csc_matrix

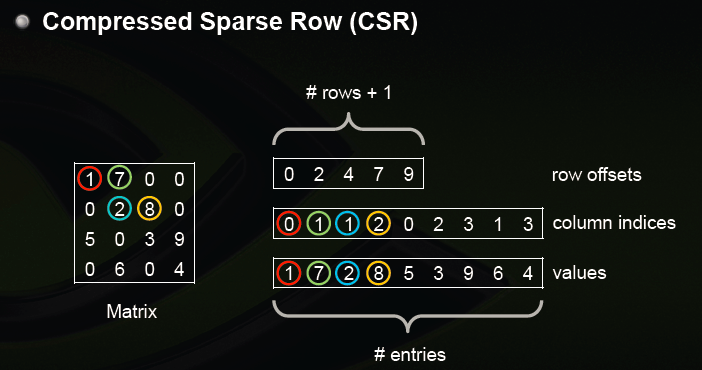
csr_matrix，全名為Compressed Sparse Row，是按行對矩陣進行壓縮的。CSR需要三類資料：數值，列號，以及行偏移量。CSR是一種編碼的方式，其中，數值與列號的含義，與coo裡是一致的。行偏移表示某一行的第一個元素在values裡面的起始偏移位置。
同樣在網路上找了一張圖，能比較好反映其中的原理。

看看在python裡怎麼使用：

>>> from scipy.sparse import csr_matrix
>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 2],
       [0, 0, 3],
       [4, 5, 6]])

怎麼樣，是不是也不是很難理解。
我們再看看文件中是怎麼說的

 Notes
 |  -----
 |
 |  Sparse matrices can be used in arithmetic operations: they support
 |  addition, subtraction, multiplication, division, and matrix power.
 |
 |  Advantages of the CSR format
 |    - efficient arithmetic operations CSR + CSR, CSR * CSR, etc.
 |    - efficient row slicing
 |    - fast matrix vector products
 |
 |  Disadvantages of the CSR format
 |    - slow column slicing operations (consider CSC)
 |    - changes to the sparsity structure are expensive (consider LIL or DOK)

不難看出，csr_matrix比較適合用來做真正的矩陣運算。
至於csc_matrix，跟csr_matrix類似，只不過是基於列的方式壓縮的，不再單獨介紹。

6.bsr_matrix