線性代數一(基本概念)
一、線性代數基本知識:
1、線性:
數乘運算與加法運算 呈現 線性。
2、
二、向量:
1、向量的表示方法:
 其中的 i、j、k是座標軸方向的單位向量。
其中的 i、j、k是座標軸方向的單位向量。
2、向量的模:
用座標計算的方法:
3、向量的運算:
(1)向量的加法減法:
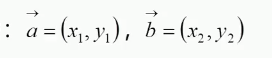
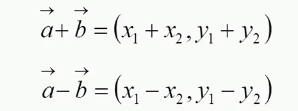
(2)向量的數乘:
 拉格朗日乘數法的 基礎 公式。
拉格朗日乘數法的 基礎 公式。
(3)向量的數量積(點積、內積):
![]()
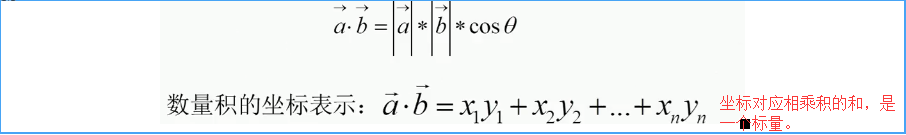
(4)向量的的向量積(外積、叉積):


(5)正交向量:

三、矩陣基本知識:
- 理解:矩陣是一個向量組,由許多 行向量 和 縱向量 組成。
- 矩陣方程求解 用增廣矩陣初等變換化為 E 。齊次/非齊次方程組 的解用 初等變化 化為 行最簡階梯型。
- 初步認為由多元一次方程組的係數組成(區別於矩陣初等變換求解矩陣方程)。矩陣是一種線性變換,可以將一些向量轉化為另一種向量。
2、矩陣的直觀感受:

3、矩陣與向量:
理解:A(m*n)每一行 或者 每一列 都屬於 向量。

四、矩陣的分類:
1、相等矩陣:
①矩陣的形狀相同(行數的列數)
②對應元素相同。
2、同形矩陣:
矩陣的形狀相同。
3、方陣:
只有方陣才具有對角線。
矩陣A中 m = n,稱之為方陣。
![]()

4、負矩陣、上三角矩陣、下三角矩陣:

5、對角矩陣:是方陣
![]()
1、對角矩陣的展示:可以用 上尖角 符號表示,如下:

2、對角矩陣的跡: trA

7、單位矩陣:常常用 E或I 來表示。它是一個方陣。
特性:A * E = A (A的列 = E 的行數)任何 矩陣 * 單位矩陣都是它本身。

8、零矩陣:
記號用 0 來表示。

9、對稱矩陣:方陣
![]()
注意:對稱矩陣一定是方陣(只有方陣才有對角線)。

五、矩陣的運算:
1、矩陣的加減:
前提:兩個矩陣必須是同形矩陣。
矩陣加減具有交換律,矩陣矩陣相乘沒有交換律。
計算結果:元素級運算。

2、矩陣的數乘:
計算結果:元素級運算。這裡要區別與行列式的數乘。
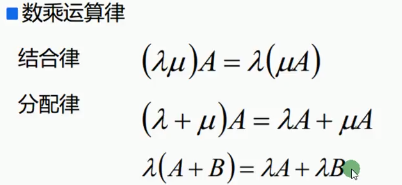
3、矩陣與向量的乘法:
前提:矩陣的列數等於向量的行數。
計算方式:左行 * 右列 對應元素乘積的和。

4、矩陣與矩陣的乘法:
得到的新矩陣由 左行右列 決定 行與列。即:(m*n)* (n*s) >>>> (m*s)

- 注意:矩陣與矩陣的乘法中沒有交換律: AB != BA(A B 互逆除外 )
- 當A逆矩陣存在時時:AC = AD >>>>> C = D 原因:並不是消去律,而是兩邊同時 乘上 A的逆矩陣化簡。

5、矩陣的轉置:
理解:對角線翻轉。

轉置的性質:

六、行列式基本知識:
1、行列式的特性:
理解:矩陣的一種運算方式。
①行列式一定是個方陣。
![]()
2、行列式的計算方法:
定義:所有不同行不同列的元素組合乘積的和。
(1)通過行列式的定義去計算:對角法則。

①逆序數的概念:t
![]()
![]()

(2)利用行列式的性質將行列式轉化為上三角行列式:
轉化時:從下到下,從左向右。
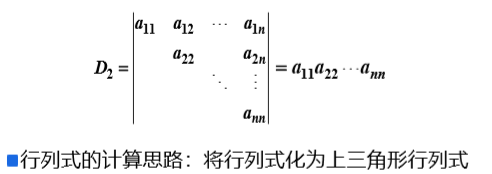
①行列式的性質 :
性質一:
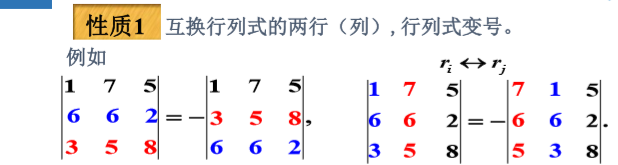
性質二:行列式的數乘(一定要區別於矩陣的數乘)

性質三:行列式如果某一行或某一列與另一行或者另一列存在倍數或者相同,行列式的數值為零。
性質四:行列式之間的加法:
前提:①兩個行列式形狀相同。
②兩個行列式僅有一行或一列的元素不相同。
結果:相同元素覆蓋照抄,不同的行的元素對應相加。
性質五:

(3)根據某行或者某列的代數餘子式展開:
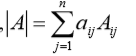
3、行列式餘子式和代數餘子式:

4、伴隨矩陣:

表示式結論: A 是一個 n階 方陣。E 單位矩陣。該結果是一個對角矩陣,對角線的元素都是 | A | 的 值。
A 是一個 n階 方陣。E 單位矩陣。該結果是一個對角矩陣,對角線的元素都是 | A | 的 值。
5、方陣的逆:只有方陣才有逆。
1、可逆矩陣的定義:
- 理解:可逆方陣 <<< >>> 可以初等變換為 E 即: AB = BA = E
- 可逆方陣 <<< >>> | A | != 0

2、方陣可逆的充要條件: 兩個條件等價。
①

② 矩陣行列式的值 | A | != 0 。
3、可逆方陣的性質:


4、n階方陣逆矩陣的計算:
第一種方法:
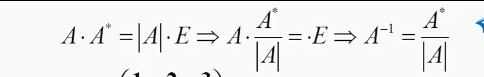
②第二種方法:
利用A 與 E 的增廣矩陣 的初等變換 >>>>>>>>>>>>>>>>>>>>>.. 求解出 A的逆矩陣。
七、矩陣的初等變換:
- 注意:矩陣換行與行列式換行不同(行列式的換行值的符號會發生變化)
- 矩陣的 初等列變換 與 初等行變換 統稱為初等變換。
- 可以通過 初等行變換 轉化為 E 的方陣為可逆方陣,否則為奇異矩陣。
矩陣初等變換的理解:線性方程組加減消元。

1、增廣矩陣:
記做: B = (A,b)

2、初等變換的性質:

2、矩陣初等變換的分類:
(1、普通的行階梯矩陣:


(2、行最簡形矩陣:
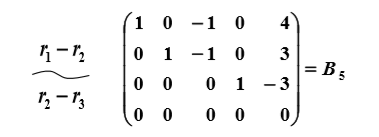



(3、標準形矩陣:
特性:



3、初等變換的定理:
其中: PA = B 是初等變化的 代數 表達形式。P是某個可逆方陣。

方陣可逆的充要條件:

4、初等變換的應用:
(1)利用初等行變換求解逆矩陣:
例:求解A 的逆矩陣:
思路:將A 與 E 建立 增廣矩陣 B , B= (A,E) >>>>> 通過初等行變換 >>>>>> (E,P) P 就是A的 可逆矩陣:P * A = E。
(2)利用初等行變換求解方程組的解:
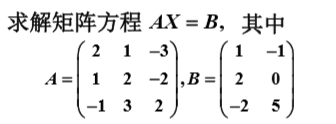
思路:類似上述求解逆矩陣的方法: ![]()
解法:增廣矩陣:

