n個元素的所有子集(遞迴+非遞迴 +不去重)
阿新 • • 發佈:2019-01-08
一、非遞迴方法
思路分析:n個元素的子集共有2^n個,其中包括空集。
(1)假設有3個元素{a, b, c},那麼此時有 2^3 個子集,即8個子集。
(2)因為有8個子集,而且包括空集,注意7對應的二進位制形式為111,並且二進位制數剛好3位;所以(000 ~ 111)可分別對應一個子集,若該位為1,則表示該元素出現在子集中,若該位為0,則表示該元素不出現在子集中;
(3)注意:001中的1在低位,對應的是a,即陣列中的首個元素。
(4)舉例
111表示子集abc;
110表示子集bc;
101表示子集ac;
100表示子集c;
011表示子集ab
010表示子集b;
001表示子集a;
000則表示空集;
具體實現如下:
#include <iostream>
using namespace std;
typedef unsigned long DWORD; // DWORD 即double world,雙位元組。
// 求arr的子集,arr共有n個元素的所有子集,時間複雜度為2^n
void print_allSubSet(int arr[],int n)
{
DWORD i,j,total,mask;
if (n > 30)
{
printf("%d is too big\n",n);
return ;
}
total= (1 列印如下:
二、遞迴方法
思路分析:同上
此處,我們新增一個標記陣列tag,用於記錄子集中對應的元素是否出現。每輸出一個子集,結束當前步驟,並進入下一步,直至遞迴完畢。
具體實現如下:
#include <iostream>
using namespace std;
// 遞迴
void allSubSet(int arr[], int tag[], int n)
{
if(n == 3)
{
cout<< "{ ";
for(int i = 0; i < 3; i++)
if(tag[i] == 1)
cout << arr[i] << ' ';
cout<< "}" << endl;
return;
}
tag[n] = 0;
allSubSet(arr, tag, n+1);
tag[n] = 1;
allSubSet(arr, tag, n+1);
}
int main(int argc, const char * argv[]) {
int a[3]={1,2,3};
int tag[3];
allSubSet(a,tag,0);
return 0;
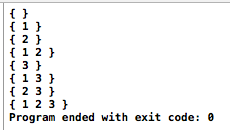
}輸出如下: