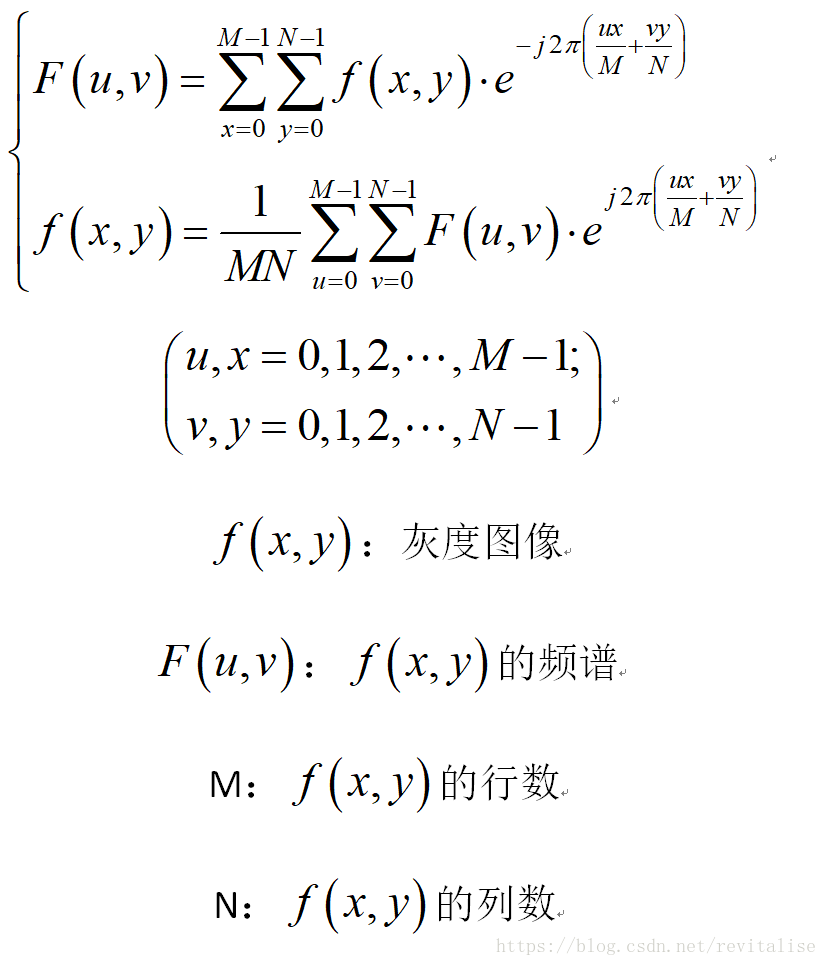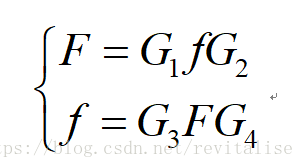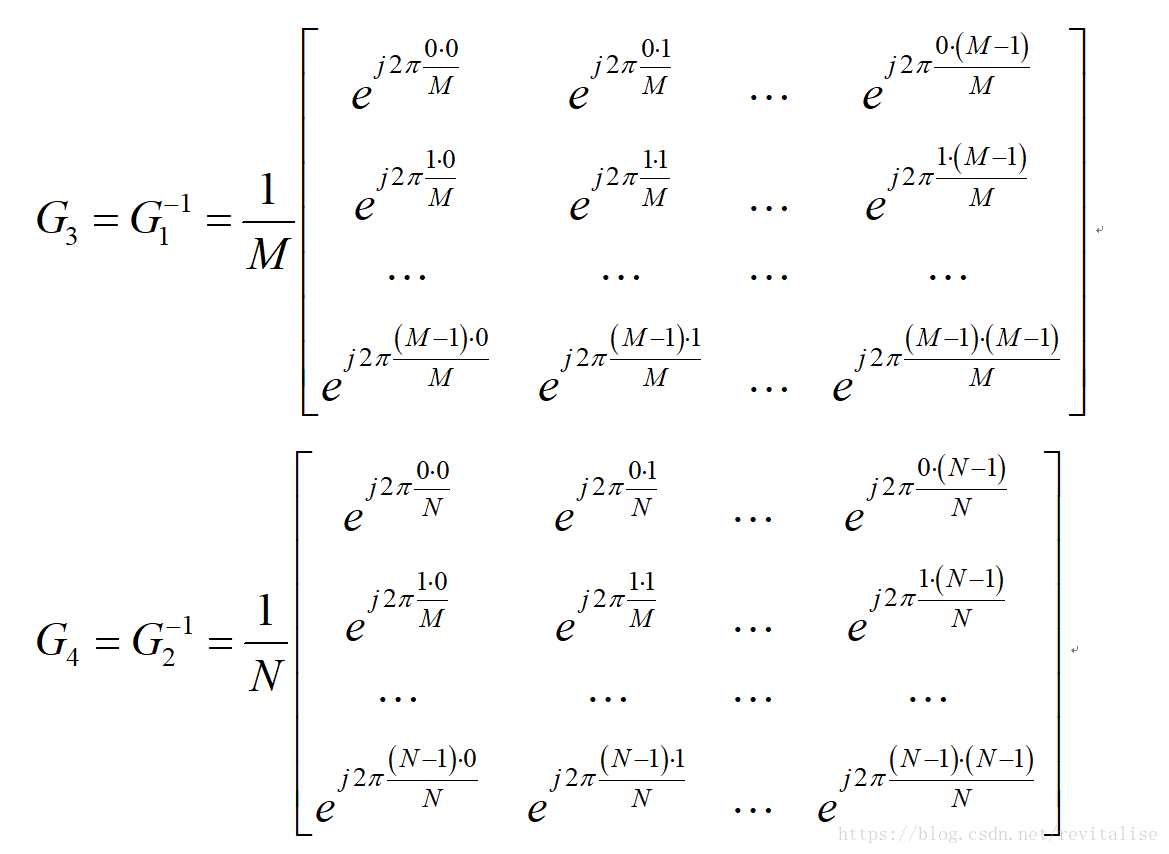二維離散傅立葉變換 matlab
阿新 • • 發佈:2019-01-08
從數學意義上看,傅立葉變換試講一個影象轉換為一系列周期函式來處理的。從物理效果上看,傅立葉變換從空間域轉換到頻率域。換句話說傅立葉變換是將影象的灰度分佈函式轉換為影象的頻率分佈函式。實際上對影象進行二維傅立葉變換得到頻譜圖,就是影象梯度的分佈圖,傅立葉頻譜圖上看到的明暗不一的亮點就是某一點與領域差異的強弱,即梯度的大小(該點的頻率大小)。
一.原理
1、代數形式的傅立葉變換:
2、矩陣形式的二維離散傅立葉變換:
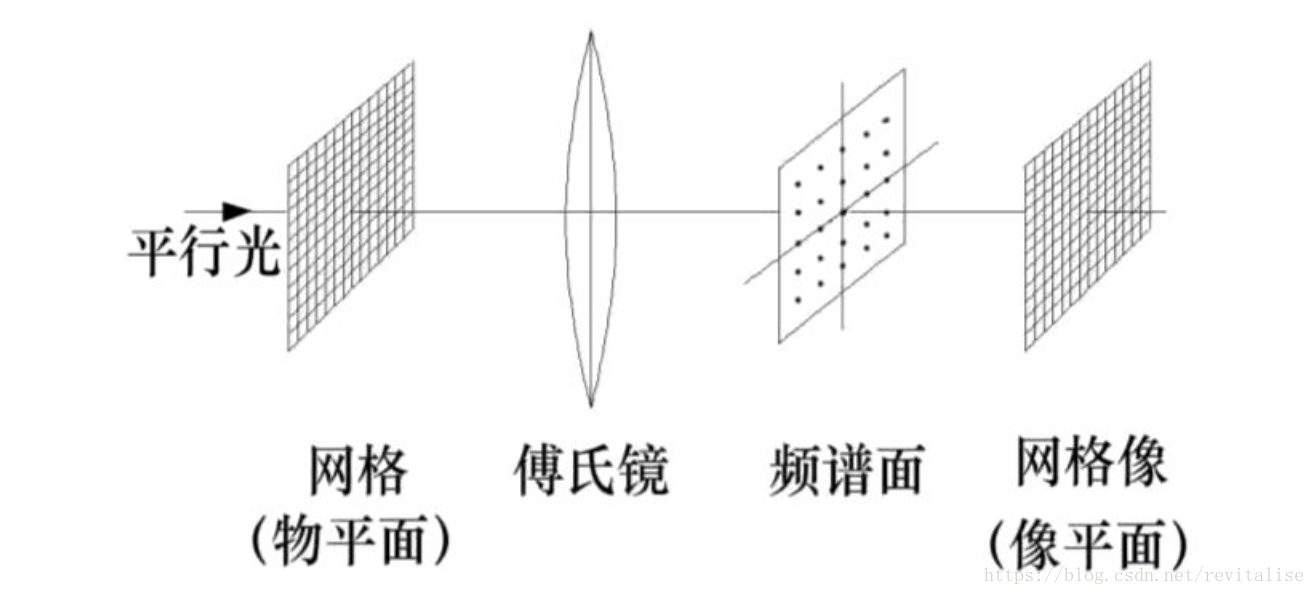
傅立葉變換不管是在影象處理中還是在科研中都有著很多的用處。例如在阿貝波特空間濾波實驗中,就使用了透鏡將影象從空間域轉換到頻率域進行濾波從而實現一系列的變換效果。
二、傅立葉變換的應用
通過傅立葉變換將影象從事於轉換到頻域,然後進行相應的處理,例如濾波和增強等,然後再通過傅立葉反變換將影象從頻域轉換到時域,就可以實現影象的處理。 在這裡 介紹一種濾波器:
用低通濾波處理影象:
可以看到濾波器的截止頻率越低,影象越模糊;截止頻率越高,濾波的效果越好。
程式:
i=imread('F:\matlab\MATLAB上機操作\圖形\data\cameraman.tif'); i=im2double(i); j=fftshift(fft2(i)); [x,y]=meshgrid(-128:127,-128:127);%產生離散資料 z=sqrt(x.^2+y^2); d1=10;d2=60;%濾波器截止頻率 n=6;%濾波器的階數 h1=1./(1+(z/d1).^(2*n)); h2=1./(1+(z/d2).^(2*n)); k1=j.*h1; k2=j.*h2; l1=ifft2(ifftshift(k1)); l2=ifft2(ifftshift(k2)); figure subplot(131);imshow(i);title('orignal') subplot(132);imshow(real(l1));title('10Hz') subplot(133);imshow(real(l2));title('60Hz')