影象傅立葉變換

二維離散傅立葉變換是將影象從空間域轉至頻域，在影象增強、影象去噪、影象邊緣檢測、影象特徵提取、影象壓縮等等應用中都起著極其重要的作用。理論基礎是任意函式都可以表示成正弦函式的線性組合的形式。公式如下

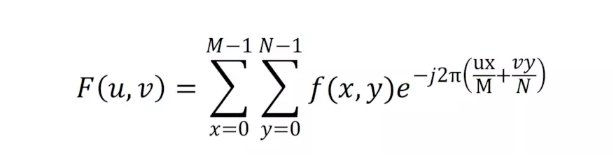
逆變換公式如下

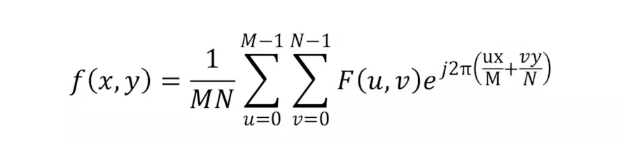
令 R(u,v) 和 I(u,c) 分別表示 F(u,v) 的實部和虛部。
幅度譜為

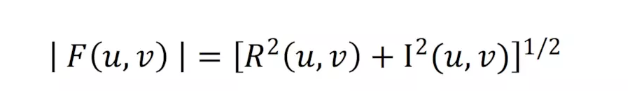
相位譜為

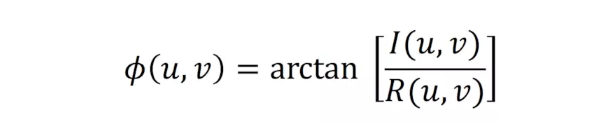
指數表示

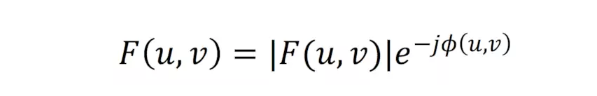
功率譜為

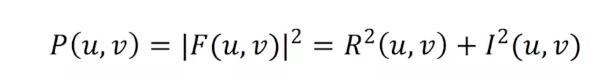
示例演示

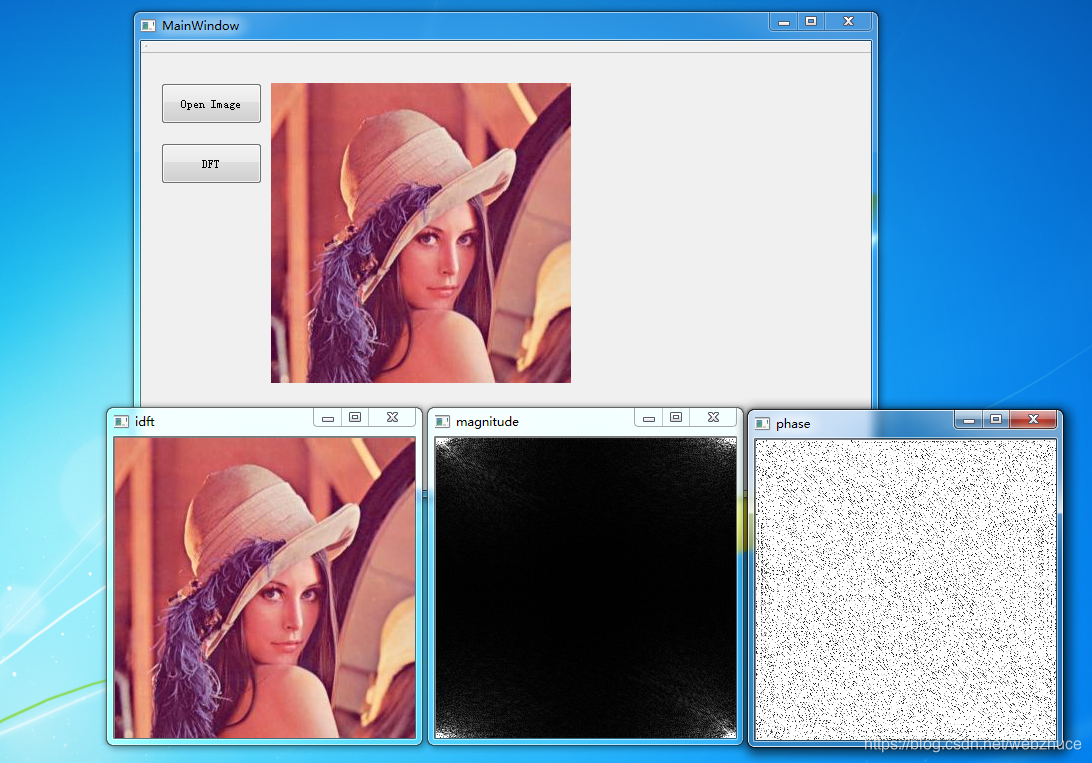
首先我們演示下，從一幅影象得到其的幅度譜和相位譜，然後再根據幅度譜和相位譜還原影象。程式碼如下。

void MainWindow::dftTransform(cv::Mat &image)
{
    image.convertTo(image, CV_32F);
    std::vector<cv::Mat> channels;
    split(image, channels);  //分離影象的RGB通道，
    cv::Mat image_B = channels[0]; //OpenCV:BGR
    //expand input image to optimal size
    int m1 = cv::getOptimalDFTSize(image_B.rows);  //選取最適合做fft的寬和高
    int n1 = cv::getOptimalDFTSize(image_B.cols);
    cv::Mat padded;
    //填充0
    cv::copyMakeBorder(image_B, padded, 0, m1 - image_B.rows, 0, n1 - image_B.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));
    cv::Mat planes[] = { cv::Mat_<float>(padded), cv::Mat::zeros(padded.size(), CV_32F) };
    cv::Mat complexI;
    cv::merge(planes, 2, complexI);  //planes[0], planes[1]是實部和虛部

    cv::dft(complexI, complexI, cv::DFT_SCALE | cv::DFT_COMPLEX_OUTPUT);
    cv::split(complexI, planes);

    //定義幅度譜和相位譜
    cv::Mat ph, mag, idft;
    cv::phase(planes[0], planes[1], ph);
    cv::magnitude(planes[0], planes[1], mag);  //由實部planes[0]和虛部planes[1]得到幅度譜mag和相位譜ph

    cv::imshow("phase", ph);
    cv::imshow("magnitude", mag);
    /*
    如果需要對實部planes[0]和虛部planes[1]，或者幅度譜mag和相位譜ph進行操作，在這裡進行更改
    */


    cv::polarToCart(mag, ph, planes[0], planes[1]);  //由幅度譜mag和相位譜ph恢復實部planes[0]和虛部planes[1]
    cv::merge(planes, 2, idft);
    cv::dft(idft, idft, cv::DFT_INVERSE | cv::DFT_REAL_OUTPUT);
    image_B = idft(cv::Rect(0, 0, image.cols & -2, image.rows & -2));
    image_B.copyTo(channels[0]);
    merge(channels, image);
    image.convertTo(image, CV_8U);
    cv::imshow("idft", image);
}
 

執行結果