決策樹（decision tree） 是一種基本的分類與迴歸方法。決策樹模型呈樹形結構， 在分類問題中， 表示基於特徵對例項進行分類的過程。 它可以認為是if-then規則的集合， 也可以認為是定義在特徵空間與類空間上的條件概率分佈。 其主要優點是模型具有可讀性， 分類速度快。 學習時， 利用訓練資料， 根據損失函式最小化的原則建立決策樹模型。 預測時， 對新的資料， 利用決策樹模型進行分類。 決策樹學習通常包括3個步驟： 特徵選擇、 決策樹的生成和決策樹的修剪。 這些決策樹學習的思想主要來源於由Quinlan在1986年提出的ID3演算法和1993年提出的C4.5演算法， 以及由Breiman等人在1984年提出的CART演算法。

1. 決策樹模型與學習

分類決策樹模型是一種描述對例項進行分類的樹形結構。 決策樹由結點（node） 和有向邊（directed edge） 組成。 結點有兩種型別： 內部結點（internalnode） 和葉結點（leaf node） 。 內部結點表示一個特徵或屬性， 葉結點表示一個類。用決策樹分類， 從根結點開始， 對例項的某一特徵進行測試， 根據測試結果， 將例項分配到其子結點； 這時， 每一個子結點對應著該特徵的一個取值。 如此遞迴地對例項進行測試並分配， 直至達到葉結點。 最後將例項分到葉結點的類中。圖5.1是一個決策樹的示意圖。 圖中圓和方框分別表示內部結點和葉結點。

決策樹和歸納演算法

決策樹技術發現數據模式和規則的核心是歸納演算法。歸納是從特殊到一般的過程。
歸納推理從若干個事實中表徵出的特徵、 特性和屬性中，通過比較、 總結、 概括而得出一個規律性的結論。
歸納推理試圖從物件的一部分或整體的特定的觀察中獲得一個完備且正確的描述。 即從特殊事實到普遍性規律的結論。
歸納對於認識的發展和完善具有重要的意義。 人類知識的增長主要來源於歸納學習。
歸納學習由於依賴於檢驗資料， 因此又稱為檢驗學習。
歸納學習存在一個基本的假設：
       任一假設如果能夠在足夠大的訓練樣本集中很好的逼近目標函式， 則它也能在未見樣本中很好地逼近目標函式。該假定是歸納學習的有效性的前提條件。
歸納過程就是在描述空間中進行搜尋的過程。
歸納可分為自頂向下， 自底向上和雙向搜尋三種方式：
       自底向上法一次處理一個輸入物件。 將描述逐步一般化。直到最終的一般化描述。
       自頂向下法對可能的一般性描述集進行搜尋， 試圖找到一些滿足一定要求的最優的描述。
決策樹演算法
與決策樹相關的重要演算法包括：
CLS, ID3， C4.5， CART
演算法的發展過程
Hunt,Marin和Stone 於1966年研製的CLS學習系統， 用於學習單個概念。
1979年, J.R. Quinlan 給出ID3演算法， 並在1983年和1986年對ID3 進行了總結和簡化， 使其成為決策樹學習演算法的典型。
Schlimmer 和Fisher 於1986年對ID3進行改造， 在每個可能的決策樹節點建立緩衝區， 使決策樹可以遞增式生成， 得到ID4演算法。
1988年， Utgoff 在ID4基礎上提出了ID5學習演算法， 進一步提高了效率。
1993年， Quinlan 進一步發展了ID3演算法， 改進成C4.5演算法。
另一類決策樹演算法為CART， 與C4.5不同的是， CART的決策樹由二元邏輯問題生成， 每個樹節點只有兩個分枝， 分別包括學習例項的正例與反例。
如圖：

根據這些資訊，可以構建如右圖所示決策樹。

決策樹的基本組成部分： 決策結點、 分支和葉子。決策樹中最上面的結點稱為根結點。是整個決策樹的開始。 每個分支是一個新的決策結點， 或者是樹的葉子。每個決策結點代表一個問題或者決策，通常對應待分類物件的屬性。每個葉結點代表一種可能的分類結果。在沿著決策樹從上到下的遍歷過程中， 在每個結點都有一個測試。 對每個結點上問題的不同測試輸出導致不同的分枝， 最後會達到一個葉子結點。 這一過程就是利用決策樹進行分類的過程，利用若干個變數來判斷屬性的類別。
決策樹與條件概率分佈
決策樹表示給定特徵條件下類的條件概率分佈。
條件概率分佈定義在特徵空間的一個劃分(partition)上。將特徵空間劃分為互不相交的單元(cell)或區域(region),並在每個單元定義一個類的概率分佈就構成了一個條件概率分佈。
決策樹的一條路徑對應於劃分中的一個單元。
決策樹所表示的條件概率分佈由各個單元給定條件下類的條件概率分佈組成。

決策樹學習本質上是從訓練資料集中歸納出一組分類規則， 與訓練資料集不相矛盾的決策樹。
能對訓練資料進行正確分類的決策樹可能有多個， 也可能 一個也沒有.我們需要的是一個與訓練資料矛盾較小的決策樹， 同時具有很好的泛化能力。
決策樹學習是由訓練資料集估計條件概率模型.基於特徵空間劃分的類的條件概率模型有無窮多個。
我們選擇的條件概率模型應該不僅對訓練資料有很好的擬合， 而且對未知資料有很好的預測。

2. 特徵選擇

決策樹的CLS演算法

CLS（Concept Learning System） 演算法
CLS演算法是早期的決策樹學習演算法。 它是許多決策樹學習演算法的基礎
CLS基本思想
從一棵空決策樹開始， 選擇某一屬性（分類屬性） 作為測試屬性。 該測試屬性對應決策樹中的決策結點。 根據該屬性的值的不同， 可將訓練樣本分成相應的子集：
       如果該子集為空， 或該子集中的樣本屬於同一個類， 則該子集為葉結點，
       否則該子集對應於決策樹的內部結點， 即測試結點， 需要選擇一個新的分類屬性對該子集進行劃分， 直到所有的子集都為空或者屬於同一類。

演算法步驟：

生成一顆空決策樹和一張訓練樣本屬性集;
若訓練樣本集T 中所有的樣本都屬於同一類,則生成結點T , 並終止學習演算法;否則
根據某種策略從訓練樣本屬性表中選擇屬性A 作為測試屬性, 生成測試結點A
若A的取值為v1,v2,…,vm, 則根據A 的取值的不同,將T 劃分成 m個子集T1,T2,…,Tm;
從訓練樣本屬性表中刪除屬性A;
轉步驟2, 對每個子集遞迴呼叫CLS;

CLS的演算法相對簡單，其實就是構建一棵樹，每行資料就是一條路徑。

CLS演算法問題：
根據某種策略從訓練樣本屬性表中選擇屬性A作為測試屬性。 沒有規定採用何種測試屬性。 實踐表明，測試屬性集的組成以及測試屬性的先後對決策樹的學習具有舉足輕重的影響。

資訊增益
Shannon在1948年提出的資訊理論理論：
熵(entropy)： 資訊量大小的度量， 即表示隨機變數不確定性的度量。
熵的通俗解釋： 事件的資訊量可如下度量：

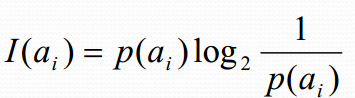
其中表示事件發生的概率。
假設有n個互不相容的事件a1,a2,a3,….,an,它們中有且僅有一個發生， 則其平均的資訊量(熵)可如下度量：

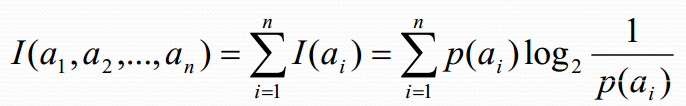
熵的理論解釋
設X是一個取有限個值的離散隨機變數， 其概率分佈為：

則隨機變數X的熵定義為：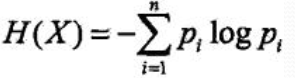
對數以2為底或以e為底(自然對數)， 這時熵的單位分別稱作位元(bit)或納特(nat),熵只依賴於X的分佈， 與X的取值無關：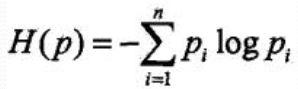

熵越大， 隨機變數的不確定性越大：
當X為1,0分佈時：
熵：

設有隨機變數(X,Y),其聯合概率分佈為：
條件熵H(Y|X)： 表示在己知隨機變數X的條件下隨機變數Y的不確定性， 定義為X給定條件下Y的條件概率分佈的熵
對X的數學期望：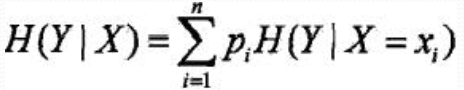
當熵和條件熵中的概率由資料估計（特別是極大似然估計）得到時， 所對應的熵與條件熵分別稱為經驗熵（empirical
entropy)和經驗條件熵（empirical conditional entropy )
資訊增益定義:特徵A對訓練資料集D的資訊增益，g(D,A), 定義為集合D的經驗熵H(D)與特徵A給定條件下D的經驗條件熵H(D|A)之差， 即
(Information gain)表示得知特徵X的資訊而使得類Y的資訊的不確定性減少的程度。
—般地， 熵H(Y)與條件熵H(Y|X)之差稱為互資訊（mutual information)。
決策樹學習中的資訊增益等價於訓練資料集中類與特徵的互資訊
資訊增益的演算法
設訓練資料集為D
|D|表示其樣本容量， 即樣本個數
設有K個類Ck, k = 1,2， …K，
|Ck |為屬於類Ck的樣本個數
特徵A有n個不同的 取值{a1,a2…an}根據特徵A的取值將D劃分為n個子集D1.。 。 Dn
|Di|為 Di的樣本個數
記子集Di中屬於類Ck的樣本集合為Dik
|Dik|為Dik的樣本個數
輸入： 訓練資料集D和特徵A；
輸出： 特徵A對訓練資料集D的資訊增益g(D,A)
1、 計算資料集D的經驗熵H(D)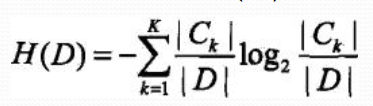
2、 計算特徵A對資料集D的經驗條件熵H(D|A)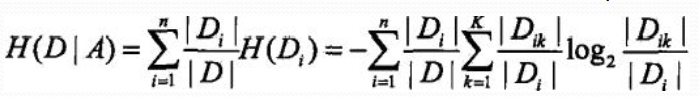
3、 計算資訊增益

3. 決策樹的生成

ID3演算法

ID3演算法是一種經典的決策樹學習演算法， 由Quinlan於1979年提出。
ID3演算法主要針對屬性選擇問題。 是決策樹學習方法中最具影響和最為典型的演算法。
該方法使用資訊增益度選擇測試屬性。
當獲取資訊時， 將不確定的內容轉為確定的內容， 因此資訊伴著不確定性。
從直覺上講， 小概率事件比大概率事件包含的資訊量大。 如果某件事情是“百年一見” 則肯定比“習以為常” 的事件包含的資訊量大。
 如何度量資訊量的大小？
答： 資訊增益
在決策樹分類中， 假設S是訓練樣本集合， |S|是訓練樣
本數， 樣本劃分為n個不同的類C1,C2,….Cn， 這些類的
大小分別標記為|C1|， |C2|， …..,|Cn|。 則任意樣本S屬
於類Ci的概率為：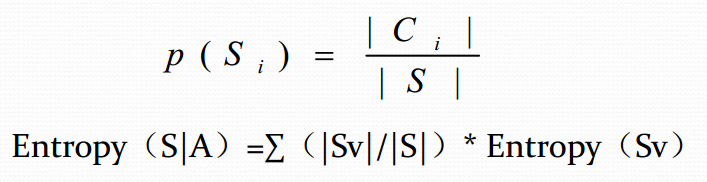

∑是屬性A的所有可能的值v, Sv是屬性A有v值的S子集
|Sv|是Sv 中元素的個數； |S|是S中元素的個數。
下面舉例計算資訊增益：

第1步：

第二步：

第三步：

第四步：

第五步：

直接上程式碼：

import math
data_list = [
[64, '青', '高', '否', '良', '不買'],
[64, '青', '高', '否', '優', '不買'],
[128, '中', '高', '否', '良', '買'],
[60, '老', '中', '否', '良', '買'],
[64, '老', '低', '是', '良', '買'],
[64, '老', '低', '是', '優', '不買'],
[64, '中', '低', '是', '優', '買'],
[128, '青', '中', '否', '良', '不買'],
[64, '青', '低', '是', '良', '買'],
[132, '老', '中', '是', '良', '買'],
[64, '青', '中', '是', '優', '買'],
[32, '中', '中', '否', '優', '買'],
[32, '中', '高', '是', '良', '買'],
[63, '老', '中', '否', '優', '不買'],
[1, '老', '中', '否', '優', '買']
]

# 選取某列的相同特徵的資料
def get_same_column_value(column_index,value,data_list):
	new_data_list = []
	for i in data_list:
		if i[column_index] == value :
			new_data_list.append(i)
	return new_data_list
# 計算總計數
def get_total_count(data_list):
	count = 0
	for i in data_list:
		count += i[0]
	return count

# 計算熵公式
def get_entropy(p1,p2):
    if p1 == 1 and p2 == 0 or p1 == 0 and p2 == 1:
		return 0.0
	return -(p1*math.log(p1, 2)+p2*math.log(p2, 2))

# 第1步計算決策屬性的熵
c5_1,c5_2 = get_total_count(get_same_column_value(5, '買',data_list)),get_total_count(get_same_column_value(5, '不買',data_list))
p5_1,p5_2 = c5_1/(c5_1 + c5_2), c5_2/(c5_1 + c5_2)
Hd_5 = get_entropy(p5_1,p5_2)
print(Hd_5)
# 第2步計算條件屬性的熵，以年齡為例
# 計算年齡中青年的熵
c0_1_1,c0_1_2 = get_total_count(get_same_column_value(1, '青',get_same_column_value(5, '買',data_list))
),get_total_count(get_same_column_value(1, '青',get_same_column_value(5, '不買',data_list)))
p0_1_1,p0_1_2 = c0_1_1/(c0_1_1 + c0_1_2), c0_1_2/(c0_1_1 + c0_1_2)
Hd_0_1 = get_entropy(p0_1_1,p0_1_2)
print(Hd_0_1)
# 計算年齡中中年的熵
c0_2_1,c0_2_2 = get_total_count(get_same_column_value(1, '中',get_same_column_value(5, '買',data_list))
),get_total_count(get_same_column_value(1, '中',get_same_column_value(5, '不買',data_list)))
p0_2_1,p0_2_2 = c0_2_1/(c0_2_1 + c0_2_2), c0_1_2/(c0_2_1 + c0_2_2)
Hd_0_2 = get_entropy(p0_2_1,p0_2_2)
print(Hd_0_2)
# 計算年齡中老年的熵
c0_3_1,c0_3_2 = get_total_count(get_same_column_value(1, '老',get_same_column_value(5, '買',data_list))
),get_total_count(get_same_column_value(1, '老',get_same_column_value(5, '不買',data_list)))
p0_3_1,p0_3_2 = c0_3_1/(c0_3_1 + c0_3_2), c0_3_2/(c0_3_1 + c0_3_2)
Hd_0_3 = get_entropy(p0_3_1,p0_3_2)
print(Hd_0_3)
# 計算年齡的平均資訊期望
E = get_total_count(get_same_column_value(1, '青',data_list))/get_total_count(data_list)*Hd_0_1 + \
	get_total_count(get_same_column_value(1, '中',data_list))/get_total_count(data_list)*Hd_0_2 + \
	get_total_count(get_same_column_value(1, '老',data_list))/get_total_count(data_list)*Hd_0_3
print(E)
# 年齡資訊增益
G = Hd_5 - E
print(G)

執行：

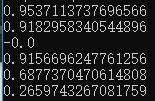
下面迴圈計算所有屬性的資訊增益：

import math
data_list = [
[64, '青', '高', '否', '良', '不買'],
[64, '青', '高', '否', '優', '不買'],
[128, '中', '高', '否', '良', '買'],
[60, '老', '中', '否', '良', '買'],
[64, '老', '低', '是', '良', '買'],
[64, '老', '低', '是', '優', '不買'],
[64, '中', '低', '是', '優', '買'],
[128, '青', '中', '否', '良', '不買'],
[64, '青', '低', '是', '良', '買'],
[132, '老', '中', '是', '良', '買'],
[64, '青', '中', '是', '優', '買'],
[32, '中', '中', '否', '優', '買'],
[32, '中', '高', '是', '良', '買'],
[63, '老', '中', '否', '優', '不買'],
[1, '老', '中', '否', '優', '買']
]

# 選取某列的相同特徵的資料
def get_same_column_value(column_index,value,data_list):
	new_data_list = []
	for i in data_list:
		if i[column_index] == value :
			new_data_list.append(i)
	return new_data_list
# 計算總計數
def get_total_count(data_list):
	count = 0
	for i in data_list:
		count += i[0]
	return count

# 計算熵公式
def get_entropy(p1,p2):
	if p1 == 1 and p2 == 0 or p1 == 0 and p2 == 1:
		return 0.0
	return -(p1*math.log(p1, 2)+p2*math.log(p2, 2))
# 計算每個屬性的特徵集合
def get_features_set(data_list):
	attr_set_list = []
	for i in range(1,5):
		attr_set = []
		for j in data_list:
			attr_set.append(j[i])
		attr_set_list.append(list(set(attr_set)))
	return attr_set_list
# 計算每個屬性的資訊增益
def get_attrs_G(features_set):
	c5_1,c5_2 = get_total_count(get_same_column_value(5, '買',data_list)),get_total_count(get_same_column_value(5, '不買',data_list))
	p5_1,p5_2 = c5_1/(c5_1 + c5_2), c5_2/(c5_1 + c5_2)
	Hd_5 = get_entropy(p5_1,p5_2)
	G_list = []
	for i in range(len(features_set)):
		E = 0
		for j in features_set[i]:
			c0_1_1,c0_1_2 = get_total_count(get_same_column_value(i + 1, j, get_same_column_value(5, '買',data_list))
			),get_total_count(get_same_column_value(i + 1, j, get_same_column_value(5, '不買',data_list)))
			p0_1_1,p0_1_2 = c0_1_1/(c0_1_1 + c0_1_2), c0_1_2/(c0_1_1 + c0_1_2)
			Hd_0_1 = get_entropy(p0_1_1,p0_1_2)
			E1 = get_total_count(get_same_column_value(i + 1, j, data_list))/get_total_count(data_list)*Hd_0_1
			E += E1
		G_list.append(Hd_5 - E)
	return G_list
print(get_attrs_G(get_features_set(data_list)))

結果：

從左到右分別是年齡、收入、學生、信譽的資訊增益，和手動計算的一致：

得到資訊增益後，對其進行排序，資訊增益最大的屬性將作息樹的根結點。此時初步構建如下圖：

可以看到中年都買，於是無需判斷，作為葉子結點。到青年這個結點，我們又要重新計算買與不買的熵，同時從feature_set移除屬性年齡，即移除青中老年，然後再按上邊的流程重新計算資訊增益並排序，直到結點是葉子結點。下面來算下青年中買與不買的熵：

如果選擇收入作為節點：

可以看到，此時計算資訊增益時，用的是青年中買與不買的熵，也就是說，只要作為結點不是葉節點，在構建時就要重新計算熵，並以此熵作為新的熵作資訊增益的計算。下面通過程式碼求出年齡結點下老，中，青的三個結點的資訊增益，程式碼在之前的程式碼作了一些調整：

import math
data_list = [
[64, '青', '高', '否', '良', '不買'],
[64, '青', '高', '否', '優', '不買'],
[128, '中', '高', '否', '良', '買'],
[60, '老', '中', '否', '良', '買'],
[64, '老', '低', '是', '良', '買'],
[64, '老', '低', '是', '優', '不買'],
[64, '中', '低', '是', '優', '買'],
[128, '青', '中', '否', '良', '不買'],
[64, '青', '低', '是', '良', '買'],
[132, '老', '中', '是', '良', '買'],
[64, '青', '中', '是', '優', '買'],
[32, '中', '中', '否', '優', '買'],
[32, '中', '高', '是', '良', '買'],
[63, '老', '中', '否', '優', '不買'],
[1, '老', '中', '否', '優', '買']
]
data_labels = ['計數','年齡','收入','學生','信譽','歸類']
# 選取某列的相同特徵的資料
def get_same_column_value(column_index,value,data_list):
	new_data_list = []
	for i in data_list:
		if i[column_index] == value :
			new_data_list.append(i)
	return new_data_list
# 計算總計數
def get_total_count(data_list):
	count = 0
	for i in data_list:
		count += i[0]
	return count

# 計算熵公式
def get_entropy(p1,p2):
	if p1 == 1 and p2 == 0 or p1 == 0 and p2 == 1 or p1 == 0 and p2 ==0:
		return 0.0
	return -(p1*math.log(p1, 2)+p2*math.log(p2, 2))

# 計算每個屬性的特徵集合
def get_features_set(data_list):
	attr_set_dict = {}
	for i in range(1,5):
		attr_set = []
		for j in data_list:
			attr_set.append(j[i])
		attr_set_dict[i] = list(set(attr_set))
	return attr_set_dict

# 計算p1,p2
def get_p1_p2(calculate_data_list1,calculate_data_list2):
	c1,c2 = get_total_count(calculate_data_list1),get_total_count(calculate_data_list2)
	if c1 == c2 and c1 == 0:
		return 0.0, 0.0
	p1,p2 = c1/(c1 + c2), c2/(c1 + c2)
	return p1,p2	
# 計算每個屬性的資訊增益
def get_attrs_G(features_set,data_list_):
	'''
	features_set:字典列表，所有屬性的每個特徵
	data_list:待計算的資料列表
	return: 排序好的元組列表
	'''
	# 計算結點的熵
	p1p2 = get_p1_p2(get_same_column_value(5, '買',data_list_),get_same_column_value(5, '不買',data_list_))
	Hd = get_entropy(p1p2[0],p1p2[1])
	G_dict= {}
	# 遍歷每個屬性計算資訊增益
	for i in features_set.keys():
		E = 0
		for j in features_set[i]:
			p1p2_ = get_p1_p2(get_same_column_value(i , j, get_same_column_value(5, '買',data_list_)),get_same_column_value(i , j, get_same_column_value(5, '不買',data_list_)))
			Hd_ = get_entropy(p1p2_[0],p1p2_[1])
			E1 = get_total_count(get_same_column_value(i , j, data_list_))/get_total_count(data_list_)*Hd_
			E += E1
		G_dict[data_labels[i]] = Hd - E		
	return sorted(G_dict.items(), key=lambda d: d[1])
# 得到每個屬性下的特徵列表
features_set = get_features_set(data_list)
# 得到作為根結點的屬性元組
remove_feature_g = get_attrs_G(features_set,data_list)[-1]
# 得到作為根結點的屬性名稱
remove_attr = remove_feature_g[0]
# 得到作為根結點的屬性索引
remove_attr_index = data_labels.index(remove_attr)
# 得到作為根結點的屬性特徵列表
remove_attr_features = features_set[remove_attr_index]
# 得到每個屬性下的特徵列表下刪除根結點屬性特徵列表
del features_set[remove_attr_index]
for i in remove_attr_features:
	print(i +' 的資訊增益：' + str(get_attrs_G(features_set,get_same_column_value(remove_attr_index,i,data_list))))

結果：

可以看到，青年在收入屬性下的資訊增益為0.4591，和手動算的一樣，中年結點就是葉子結點，而老年結點應該選擇信譽作為下一個屬性結點，青年將選擇學生作為下一個屬性結點。在下個結點尋找資訊增益繼續做迴圈即可。

ID3演算法-流程

1 決定分類屬性；
2 對目前的資料表， 建立一個節點N
3 如果資料庫中的資料都屬於同一個類， N就是樹葉， 在樹葉上標出所屬的類
4 如果資料表中沒有其他屬性可以考慮， 則N也是樹葉， 按照少數服從多數的原則在樹葉上標出所屬類別
5 否則， 根據平均資訊期望值E或GAIN值選出一個最佳屬性作為節點N的測試屬性
6 節點屬性選定後， 對於該屬性中的每個值：
從N生成一個分支， 並將資料表中與該分支有關的資料收集形成分支節點的資料表， 在表中刪除節點屬性那一欄如果分支數
據表非空， 則運用以上演算法從該節點建立子樹。

ID3演算法-實際使用需要注意：

Data cleaning 刪除/減少noise，補填missing values
Data transformation
資料標準化（data normalization）
資料歸納（generalize data to higher-level concepts using concept hierarchies）
例如： 年齡歸納為老、 中、 青三類，控制每個屬性的可能值不超過七種（最好不超過五種）
Relevance analysis
對於與問題無關的屬性： 刪
對於屬性的可能值大於七種又不能歸納的屬性： 刪
ID3演算法-小結

ID3演算法的基本思想是， 以資訊熵為度量， 用於決策樹節點的屬性選擇， 每次優先選取資訊量最多的屬性， 亦即能使熵值變為最小的屬性， 以構造一顆熵值下降最快的決策樹， 到葉子節點處的熵值為0。 此時， 每個葉子節點對應的例項集中的例項屬於同一類。
關於ID3決策樹構建的程式碼，我就不重新給了，網上到處都是，理解資訊增益的演算法，自己構造決策樹應該問題不大，Node class應該要有root結點，屬性，屬性特徵，已有的樹，還在結果表現形式就行。實在不行就參考這個大神的https://github.com/wzyonggege/statistical-learning-method/blob/master/DecisonTree/DT.ipynb

C4.5的生成演算法

4. 決策樹的剪枝

通過極小化決策樹整體的損失函式或代價函式來實現。
設樹T的葉結點個數為|T|,t是樹T的葉結點， 該葉結點有Nt個樣本點， 其中k類的樣本點有Ntk個， k=1,2..K,Ht(T)為葉結點t上的經驗熵， α≥0為引數， 損失函式：
經驗熵：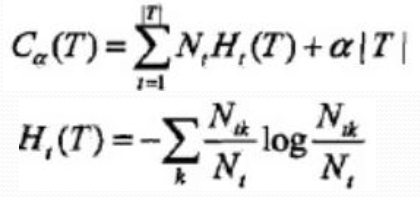
原式第一項：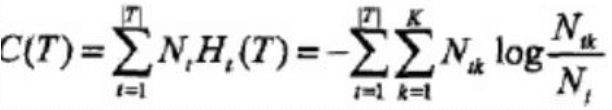
則：

樹的剪枝演算法：
設一組葉結點回縮到其父結點之前與之和的損失函式分別為：
如果： 則進行剪枝

5. ＣＡＲＴ演算法

決策樹面臨的問題
理想的決策樹有三種：
(1)葉子結點數最少；
(2)葉子結點深度最小；
(3)葉子結點數最少且葉子結點深度最小。
然而， 洪家榮等人已經證明了要找到這種最優的決策樹是NP難題。 因此， 決策樹優化的目的就是要找到儘可能趨向於最優的決策樹。
過度擬合
決策樹演算法增長樹的每一個分支的深度， 直到恰好能對訓練樣例比較完美地分類。 實際應用中， 當資料中有噪聲或訓練樣例的數量太少以至於不能產生目標函式的有代表性的取樣時， 該策略可能會遇到困難。
 在以上情況發生時， 這個簡單的演算法產生的樹會過渡擬合訓練樣例（過渡擬合： Over Fitting）
對學習演算法是否成功的真正測試是看它對於訓練中未見到的資料的執行效能。 訓練過程應該包含訓練樣本和驗證樣本。 驗證樣本用於測試訓練後的效能。 如果驗證結果差， 則需要考慮採用不同的結構重新進行訓練， 例如使用更大的樣本集， 或者改變從連續值到離散值得資料轉換等。
通常應該建立一個驗證過程， 在訓練最終完成後用來檢測訓練結果的泛化能力。
一般可以將分類模型的誤差分為：
1、 訓練誤差（Training Error） ；
2、 泛化誤差（Generalization Error）
訓練誤差是在訓練記錄上誤分類樣本比例；
泛化誤差是模型在未知記錄上的期望誤差；
一個好的模型不僅要能夠很好地擬合訓練資料， 而且對未知樣本也要能夠準確地分類。
 一個好的分類模型必須具有低的訓練誤差和泛化誤差。 因為一個具有低訓練誤差的模型， 其泛化誤差可能比具有較高訓練誤差的模型高。 （訓練誤差低， 泛化誤差高， 稱為過渡擬合）
決策樹演算法比較適合處理離散數值的屬性。 實際應用中屬性是連續的或者離散的情況都比較常見。
在應用連續屬性值時， 在一個樹結點可以將屬性Ai的值劃分為幾個區間。 然後資訊增益的計算就可以採用和離散值處理一樣的方法。 原則上可以將Ai的屬性劃分為任意數目的空間。 C4.5中採用的是二元分割（BinarySplit） 。需要找出一個合適的分割閾值。
CART樹
目標變數是類別的 --- 分類樹
目標變數是連續的 --- 迴歸樹
CART與ID3的不同
二元劃分：
二叉樹不易產生資料碎片， 精確度往往也會高於多叉樹
CART中選擇變數的不純性度量：
分類目標： Gini指標、 Towing、 order Towing
連續目標： 最小平方殘差、 最小絕對殘差
剪枝：
用預剪枝或後剪枝對訓練集生長的樹進行剪枝

樹的建立：
如果目標變數是標稱的， 並且是具有兩個以上的類別， 則CART可能考慮將目標類別合併成兩個超類別（雙化） ；
如果目標變數是連續的， 則CART演算法找出一組基於樹的迴歸方程來預測目標變數。
CART演算法由兩部分組成：
決策樹生成
決策樹剪枝
迴歸樹： 平方誤差最小化
分類樹： Gini Index
迴歸樹的生成

CART生成
設Y是連續變數， 給定訓練資料集：
假設已將輸入空間劃分為M各單元R1,R2..Rm,並且每個單元Rm上有一個固定的輸出Cm， 迴歸樹表示為：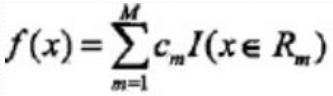
平方誤差來表示預測誤差， 用平方誤差最小準則求解每個單元上的最優輸出值：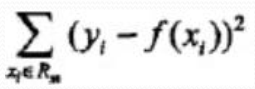
Rm上的Cm的最優值：

最小二乘迴歸樹生成演算法

分類樹的生成：
基尼指數
分類問題中， 假設有k個類， 樣本點屬於k的概率Pk，則概率分佈的基尼指數：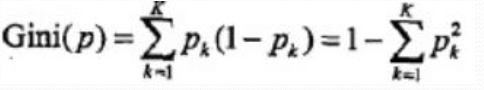
二分類問題：
對給定的樣本集合D， 基尼指數：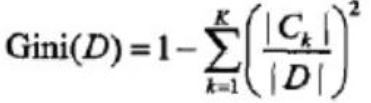

如果樣本集合D根據特徵A是否為a被分割成D1和D2，即
則在特徵A的條件下， 集合D的基尼指數：

CART生成演算法
輸入： 訓練資料集D， 停止計算條件
輸出： CART決策樹
從根節點開始， 遞迴對美國結點操作
1、 設結點資料集為D， 對每個特徵A， 對其每個值a，根據樣本點對A=a的測試為是或否， 將D分為D1， D2，計算A=a的基尼指數
2、 在所有的特徵A以及所有可能的切分點a中， 選擇基尼指數最小的特徵和切分點， 將資料集分配到兩個子結點中。
3、 對兩個子結點遞迴呼叫1， 2步驟
4、 生成CART樹
CART剪枝
1、 從生成演算法產生的決策樹T0底端開始不斷剪枝， 直到T0的根結點， 形成子樹序列{T0,T1..Tn},
2、 通過交叉驗證法在獨立的驗證資料集上對子樹序列進行測試， 從中選擇最優子樹
1、 剪枝， 形成子樹序列
剪枝過程中， 計運算元樹的損失函式：
對固定的a一定存在損失函式最小的子樹， 表示為Ta，當a變大時， 最優子樹Ta偏小，a=0時， 整體樹最優， a趨近無窮大， 單結點最優。將a從小增大， 0=

具體： 從T0開始剪枝， 以t為單結點樹的損失函式：
以t為根結點的子樹Tt的損失函式：
當a=0及a很小時，
不斷增大a， 當
Tt與t有相同損失函式值， 但t結點更少， 所以剪枝Tt。

對T0中每個內部結點t， 計算：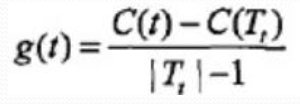
在T0中剪去g(t)最小的Tt， 將得到的子樹作為T1， 同時將最小的g(t)設為a1， T1為區間[a1,a2) 的最優子樹
如此剪枝下去， 直到根節點， 不斷增加a的值， 產生新的區間。

2、 在剪枝得到的子樹序列{T0,T1…Tn}中通過交叉驗證選取最優子樹Ta
利用獨立的驗證資料集， 測試子樹序列中各子樹的平方誤差或基尼指數， 最小的決策樹就是最優決策樹。

以上內容均出自李航老師的《統計學習方法》。