統計學習方法 k 近鄰演算法(附簡單模型程式碼)
1. k 近鄰演算法
k近鄰法(k-nearest neighbor, k-NN) 是一種基本分類與迴歸方法。 k近鄰法的輸入為例項的特徵向量, 對應於特徵空間的點; 輸出為例項的類別, 可以取多類。 k近鄰法假設給定一個訓練資料集, 其中的例項類別已定。 分類時, 對新的例項, 根據其k個最近鄰的訓練例項的類別, 通過多數表決等方式進行預測。因此, k近鄰法不具有顯式的學習過程。 k近鄰法實際上利用訓練資料集對特徵向量空間進行劃分, 並作為其分類的“模型”。 k值的選擇、 距離度量及分類決策規則是k近鄰法的三個基本要素。 k近鄰法1968年由Cover和Hart提出。
演算法(k近鄰法)
輸入: 訓練資料集
![]()
其中, xi∊x⊆Rn為例項的特徵向量, yi∊ ={c1, c2,…,cK}為例項的類別, i=1,2,…,N; 例項特徵向量x;
輸出: 例項x所屬的類y。
(1) 根據給定的距離度量, 在訓練集T中找出與x最鄰近的k個點, 涵蓋這k個點的x的鄰域記作Nk(x);
(2) 在Nk(x)中根據分類決策規則(如多數表決) 決定x的類別y:
![]()
上式中, I為指示函式, 即當yi=cj時I為1, 否則I為0。
k近鄰法的特殊情況是k=1的情形, 稱為最近鄰演算法。 對於輸入的例項點(特徵向量) x, 最近鄰法將訓練資料集中與x最鄰近點的類作為x的類。k近鄰法沒有顯式的學習過程。
2. k 近鄰模型
k近鄰法使用的模型實際上對應於對特徵空間的劃分。 模型由三個基本要素——距離度量、 k值的選擇和分類決策規則決定。
特徵空間中兩個例項點的距離是兩個例項點相似程度的反映。 k近鄰模型的特徵空間一般是n維實數向量空間Rn。 使用的距離是歐氏距離, 但也可以是其他距離, 如更一般的Lp距離(Lp distance) 或Minkowski距離(Minkowski distance) 。設特徵空間x是n維實數向量空間Rn,![]()
![]() xi,xj的Lp距離定義為:
xi,xj的Lp距離定義為: 這裡p≥1。 當p=2時, 稱為歐氏距離(Euclidean distance), 即
這裡p≥1。 當p=2時, 稱為歐氏距離(Euclidean distance), 即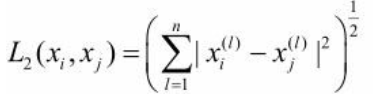 當p=1時, 稱為曼哈頓距離(Manhattan distance) , 即
當p=1時, 稱為曼哈頓距離(Manhattan distance) , 即
圖3.2給出了二維空間中p取不同值時, 與原點的Lp距離為1(Lp=1) 的點的圖形。

k值的選擇會對k近鄰法的結果產生重大影響。
如果選擇較小的k值, 就相當於用較小的鄰域中的訓練例項進行預測, “學習”的近似誤差(approximation error) 會減小, 只有與輸入例項較近的(相似的) 訓練例項才會對預測結果起作用。 但缺點是“學習”的估計誤差(estimation error) 會增大, 預測結果會對近鄰的例項點非常敏感。 如果鄰近的例項點恰巧是噪聲, 預測就會出錯。 換句話說, k值的減小就意味著整體模型變得複雜, 容易發生過擬合。
如果選擇較大的k值, 就相當於用較大鄰域中的訓練例項進行預測。 其優點是可以減少學習的估計誤差。 但缺點是學習的近似誤差會增大。 這時與輸入例項較遠的(不相似的) 訓練例項也會對預測起作用, 使預測發生錯誤。 k值的增大就意味著整體的模型變得簡單。
k近鄰法中的分類決策規則往往是多數表決, 即由輸入例項的k個鄰近的訓練例項中的多數類決定輸入例項的類。
多數表決規則(majority voting rule) 有如下解釋: 如果分類的損失函式為0-1損失函式, 分類函式為![]() 那麼誤分類的概率是
那麼誤分類的概率是![]() 。對給定的例項x∊x, 其最近鄰的k個訓練例項點構成集合Nk(x)。 如果涵蓋Nk(x)的區域的類別是cj, 那麼誤分類率是
。對給定的例項x∊x, 其最近鄰的k個訓練例項點構成集合Nk(x)。 如果涵蓋Nk(x)的區域的類別是cj, 那麼誤分類率是 要使誤分類率最小即經驗風險最小, 就要使
要使誤分類率最小即經驗風險最小, 就要使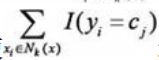 最大, 所以多數表決規則等價於經驗風險最小化。
最大, 所以多數表決規則等價於經驗風險最小化。
3. k 近鄰法的實現: kd 樹
kd樹是一種對k維空間中的例項點進行儲存以便對其進行快速檢索的樹形資料結構。kd樹是二叉樹, 表示對k維空間的一個劃分(partition) 。 構造kd樹相當於不斷地用垂直於座標軸的超平面將k維空間切分, 構成一系列的k維超矩形區域。 kd樹的每個結點對應於一個k維超矩形區域。
構造平衡kd樹
輸入: k維空間資料集T={x1, x2,…,xN},
其中 , i=1,2,…,N;
輸出: kd樹。
(1) 開始: 構造根結點, 根結點對應於包含T的k維空間的超矩形區域。
選擇x(1)為座標軸, 以T中所有例項的x(1)座標的中位數為切分點, 將根結點對應的超矩形區域切分為兩個子區域。 切分由通過切分點並與座標軸x(1)垂直的超平面實現。由根結點生成深度為1的左、 右子結點: 左子結點對應座標x(1)小於切分點的子區域,右子結點對應於座標x(1)大於切分點的子區域。將落在切分超平面上的例項點儲存在根結點。
(2) 重複: 對深度為j的結點, 選擇x(l)為切分的座標軸, l=j(modk)+1, 以該結點的區域中所有例項的x(l)座標的中位數為切分點, 將該結點對應的超矩形區域切分為兩個子區域。 切分由通過切分點並與座標軸x(l)垂直的超平面實現。由該結點生成深度為j+1的左、 右子結點: 左子結點對應座標x(l)小於切分點的子區域, 右子結點對應座標x(l)大於切分點的子區域。將落在切分超平面上的例項點儲存在該結點。
(3) 直到兩個子區域沒有例項存在時停止。 從而形成kd樹的區域劃分。
程式碼:
# kd-tree每個結點中主要包含的資料結構如下
class KdNode(object):
def __init__(self, dom_elt, split, left, right):
self.dom_elt = dom_elt # k維向量節點(k維空間中的一個樣本點)
self.split = split # 整數(進行分割維度的序號)
self.left = left # 該結點分割超平面左子空間構成的kd-tree
self.right = right # 該結點分割超平面右子空間構成的kd-tree
class KdTree(object):
def __init__(self, data):
k = len(data[0]) # 資料維度
def CreateNode(split, data_set): # 按第split維劃分資料集exset建立KdNode
if not data_set: # 資料集為空
return None
# key引數的值為一個函式,此函式只有一個引數且返回一個值用來進行比較
# operator模組提供的itemgetter函式用於獲取物件的哪些維的資料,引數為需要獲取的資料在物件中的序號
#data_set.sort(key=itemgetter(split)) # 按要進行分割的那一維資料排序
data_set.sort(key=lambda x: x[split])
split_pos = len(data_set) // 2 # //為Python中的整數除法
median = data_set[split_pos] # 中位數分割點
split_next = (split + 1) % k # cycle coordinates
# 遞迴的建立kd樹
return KdNode(median, split,
CreateNode(split_next, data_set[:split_pos]), # 建立左子樹
CreateNode(split_next, data_set[split_pos + 1:])) # 建立右子樹
self.root = CreateNode(0, data) # 從第0維分量開始構建kd樹,返回根節點
# KDTree的前序遍歷
def preorder(root):
print (root.dom_elt)
if root.left: # 節點不為空
preorder(root.left)
if root.right:
preorder(root.right)
用kd樹的最近鄰搜尋
輸入: 已構造的kd樹; 目標點x;
輸出: x的最近鄰。
(1) 在kd樹中找出包含目標點x的葉結點: 從根結點出發, 遞迴地向下訪問kd樹。 若目標點x當前維的座標小於切分點的座標, 則移動到左子結點, 否則移動到右子結點。 直到子結點為葉結點為止。
(2) 以此葉結點為“當前最近點”。
(3) 遞迴地向上回退, 在每個結點進行以下操作:
(a) 如果該結點儲存的例項點比當前最近點距離目標點更近, 則以該例項點為“當前最近點”。
(b) 當前最近點一定存在於該結點一個子結點對應的區域。 檢查該子結點的父結點的另一子結點對應的區域是否有更近的點。 具體地, 檢查另一子結點對應的區域是否與以目標點為球心、 以目標點與“當前最近點”間的距離為半徑的超球體相交。
如果相交, 可能在另一個子結點對應的區域記憶體在距目標點更近的點, 移動到另一個子結點。 接著, 遞迴地進行最近鄰搜尋;
如果不相交, 向上回退。
(4) 當回退到根結點時, 搜尋結束。 最後的“當前最近點”即為x的最近鄰點。
如果例項點是隨機分佈的, kd樹搜尋的平均計算複雜度是O(logN), 這裡N是訓練實
例數。 kd樹更適用於訓練例項數遠大於空間維數時的k近鄰搜尋。 當空間維數接近訓練實
例數時, 它的效率會迅速下降, 幾乎接近線性掃描。
程式碼:
# 對構建好的kd樹進行搜尋,尋找與目標點最近的樣本點:
from math import sqrt
from collections import namedtuple
# 定義一個namedtuple,分別存放最近座標點、最近距離和訪問過的節點數
result = namedtuple("Result_tuple", "nearest_point nearest_dist nodes_visited")
def find_nearest(tree, point):
k = len(point) # 資料維度
def travel(kd_node, target, max_dist):
if kd_node is None:
return result([0] * k, float("inf"), 0) # python中用float("inf")和float("-inf")表示正負無窮
nodes_visited = 1
s = kd_node.split # 進行分割的維度
pivot = kd_node.dom_elt # 進行分割的“軸”
if target[s] <= pivot[s]: # 如果目標點第s維小於分割軸的對應值(目標離左子樹更近)
nearer_node = kd_node.left # 下一個訪問節點為左子樹根節點
further_node = kd_node.right # 同時記錄下右子樹
else: # 目標離右子樹更近
nearer_node = kd_node.right # 下一個訪問節點為右子樹根節點
further_node = kd_node.left
temp1 = travel(nearer_node, target, max_dist) # 進行遍歷找到包含目標點的區域
nearest = temp1.nearest_point # 以此葉結點作為“當前最近點”
dist = temp1.nearest_dist # 更新最近距離
nodes_visited += temp1.nodes_visited
if dist < max_dist:
max_dist = dist # 最近點將在以目標點為球心,max_dist為半徑的超球體內
temp_dist = abs(pivot[s] - target[s]) # 第s維上目標點與分割超平面的距離
if max_dist < temp_dist: # 判斷超球體是否與超平面相交
return result(nearest, dist, nodes_visited) # 不相交則可以直接返回,不用繼續判斷
#----------------------------------------------------------------------
# 計算目標點與分割點的歐氏距離
temp_dist = sqrt(sum((p1 - p2) ** 2 for p1, p2 in zip(pivot, target)))
if temp_dist < dist: # 如果“更近”
nearest = pivot # 更新最近點
dist = temp_dist # 更新最近距離
max_dist = dist # 更新超球體半徑
# 檢查另一個子結點對應的區域是否有更近的點
temp2 = travel(further_node, target, max_dist)
nodes_visited += temp2.nodes_visited
if temp2.nearest_dist < dist: # 如果另一個子結點記憶體在更近距離
nearest = temp2.nearest_point # 更新最近點
dist = temp2.nearest_dist # 更新最近距離
return result(nearest, dist, nodes_visited)
return travel(tree.root, point, float("inf")) # 從根節點開始遞迴
p = inf為閔式距離minkowski_distance
例3.2 給定一個二維空間的資料集:![]() 構造一個平衡kd樹。
構造一個平衡kd樹。
data = [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]
kd = KdTree(data)
preorder(kd.root)
[7, 2] [5, 4] [2, 3] [4, 7] [9, 6] [8, 1]
找出距離點[3,4.5]最近的點:
ret = find_nearest(kd, [3,4.5])
print (ret)
Result_tuple(nearest_point=[2, 3], nearest_dist=1.8027756377319946, nodes_visited=4)
本程式碼同樣適用三維,使用方式一樣。
以上內容均出自李航老師的《統計學習方法》。
