平行投影與透視投影的關係與統一的矩陣表示
D3DXMatrixShadow 產生一個矩陣,把幾何體投影到平面上,神奇的是這個矩陣不論對平行光還是點光,都具有統一的形式(見左邊D3DXMatrixShadow的文件連結)。
Introduction to 3D Game Programming with DirectX9.0 模板緩衝區那一章裡提示感興趣的讀者參考Chapter 6, “Me and My (Fake) Shadow,” Jim Blinn’s Corner: A Trip Down the Graphics Pipeline。
《計算機圖形學與幾何造型導論》用很基本的向量和矩陣(線性代數)的知識,分別推匯出了平行投影和透視投影各自的變換矩陣。因為後者我很早就讀過了,非常熟悉;只把前者簡單地看了看,有了一個思路(隨著點光源距離平面越來越遠,平面上任意兩點接收到的光線趨於平行,若點光源位置無窮遠,則就是平行光了),把這兩個變換矩陣合二為一。
齊次座標
一維
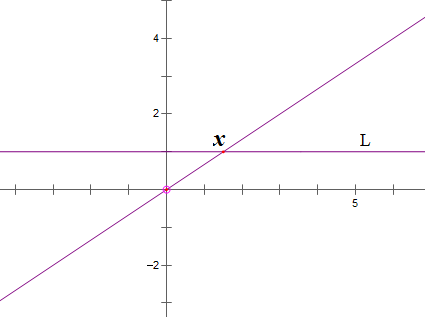
數軸L上一點的座標 x = x/1 = kx/k ( k!=0 ) 即數軸上一點的座標可以寫成兩個實數 X、k 的比值,記作 (X,k) k!=0,這就是一維空間點的齊次座標(比例關係X:k)。
(x,1) 與 k!=0 k(x,1)=(kx,k) 都是數軸L上的同一個點,對應著二維空間中的一條過原點、斜率不為零的直線(除去原點)。
(X,k) k!=0 代表數軸L上的點 x=X/k,若X!=0,k->0 x-> infinity,即無窮遠。記 (X,0) X!=0 代表無窮遠,對應著二維空間中過原點、斜率為零的直線(除去原點)。
而剩下的 (0,0) 對應著 二維空間的 原點。
二維
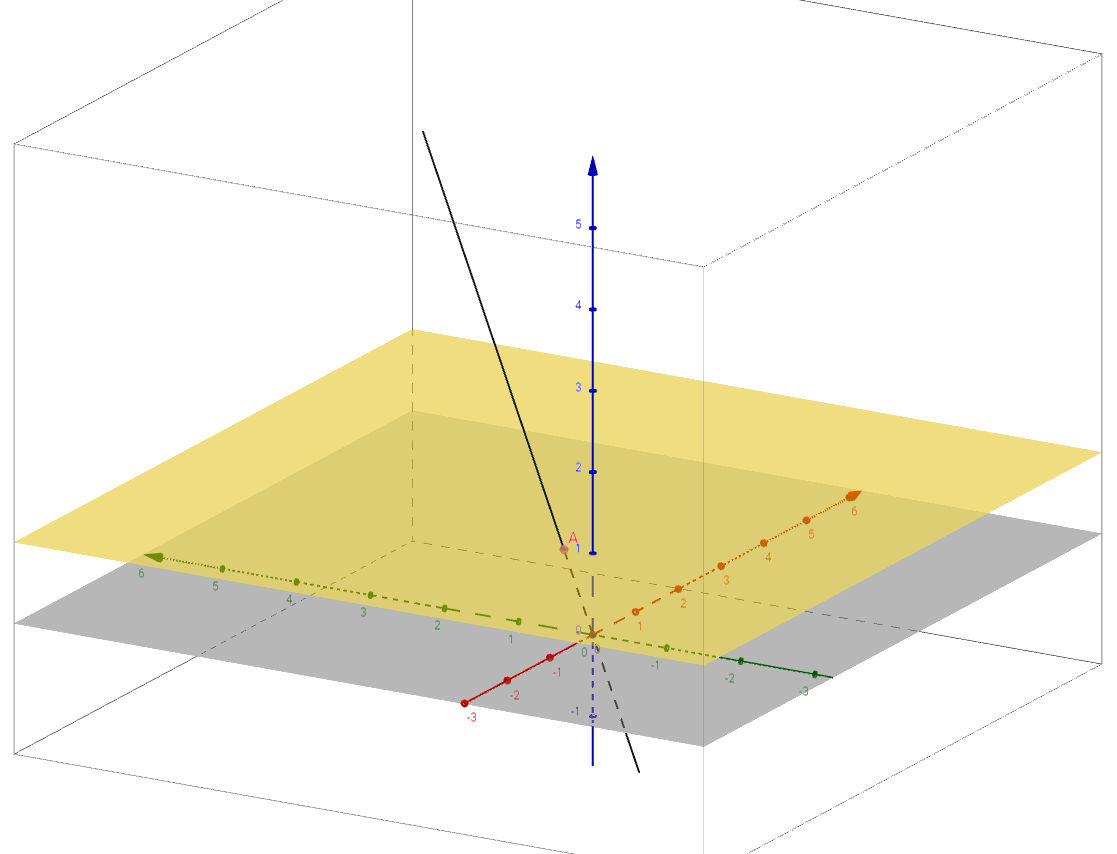
黃色平面(z=1)上某點A的二維座標 (x,y) = (x/1, y/1) = (kx/k, ky/k) k!=0,kx=X,ky=Y,寫成齊次座標的形式:(X, Y, k) <--> (X/k, Y/k, 1) = (x,y,1) k!=0,比例關係 (X: Y :k) 。
(x,y,1) 與 (kx,ky,k) k!=0 都表示黃色平面上的同一個點,對應著三維空間中一條過原點、不在xoy平面(灰色)內的直線(除去原點)。
(X, Y, k) k!=0 代表黃色平面上的點(x,y) x=X/k, y=Y/k,k->0, 若X,Y不同時為零,(x,y)= (X,Y)*(1/k) 沿(X,Y)方向趨於無窮遠。記 (X,Y,0)代表無窮遠,對應著三維空間中過原點、在xoy平面上、方向向量是(X,Y)的直線(除去原點)
而剩下的 (0,0,0) 對應著 三維空間的 原點。
在黃色平面這個二維世界中,A是一個點光源,它的齊次座標為 (a,b,w),即二維座標為 (a/w,b/w) = (a,b)*(1/w),當w->0時,點A不斷沿著平行於向量(a,b)的方向(與向量(a,b)的方向相同或相反)向遠處移動,最後趨於黃色平面上向量(a,b)方向的直線兩端的無窮遠。此時A就是一個平行光了,方向是(a,b)。記作(a,b,0)。(a,b,0) 與 (ka,kb,0) k!=0 產生的平行光線是一樣的。
這樣平行光、點光源就用齊次座標統一起來了:(a,b,w) w!=0 時,代表(a/w,b/w)位置的點光源;w=0且a、b不同時為零,代表平行於向量(a,b)的平行光。(0,0,0)含義未定義。
無窮遠 對應 一組共線的非零向量。
同理可以推廣到三維空間、更高維度幾何空間點的齊次座標,運用代數。
投影矩陣
平行投影
投影平面過Q點,法向是N,平行光線的方向向量為u(光線與平面不平行),則投影矩陣 Parallel(Q,N,u) 為(證明見附錄),矩陣的值與被變換的點P(x,y,z,1)無關:
$$\begin{bmatrix}
I-\frac{N^\top u}{uN^\top} & 0 \\ \\
\frac{QN^\top}{uN^\top}u & 1 \\
\end{bmatrix}$$
透視投影
投影平面過Q點,法向是N,點光源的位置為u,則投影矩陣 Perspective(Q,N,u) 為(證明見附錄),矩陣的值與被變換的點P(x,y,z,1)無關:$$\begin{bmatrix}
(u-Q)N^\top I-N^\top u & -N^\top \\ \\
QN^\top u & uN^\top \\
\end{bmatrix}$$
齊次形式
(x,y,z,1) Parallel(Q,N,u) = (x',y',z',1)
(x,y,z,1) Parallel(Q,N,u)uN^T = (x',y',z',1) uN^T ~ (x',y',z';1)
$$Parallel(Q,N,u)uN^\top=\begin{bmatrix}uN^\top I-N^\top u & 0 \\ \\QN^\top u & uN^\top \\\end{bmatrix}$$
> Parallel(Q,N,u)uN^T也是平面Q,N和平行光u的平行投影矩陣。
點光源的位置是u,若表示成齊次座標(S,w),w是任意不為零的常數,則u=S/w,代入Perspective(Q,N,u)得:
$$Perspective(Q,N,S,w)=\begin{bmatrix}
(\frac{1}{w}S-Q)N^\top I-\frac{1}{w}N^\top S & -N^\top \\ \\
\frac{1}{w}QN^\top S & \frac{1}{w}SN^\top \\
\end{bmatrix}\quad w\neq 0$$
(x,y,z,1) Perspective(Q,N,S,w) = (X,Y,Z,k) ~ (X/k,Y/k,Z/k,1)
(x,y,z,1) Perspective(Q,N,S,w) w = (X,Y,Z,k) w ~ (X/k,Y/k,Z/k,1)w!=0
$$Perspective(Q,N,S,w)w=\begin{bmatrix}
(S-wQ)N^\top I-N^\top S & -wN^\top \\ \\
QN^\top S & SN^\top \\
\end{bmatrix}\quad w\neq 0$$
> w!=0,Perspective(Q,N,S,w) w 是平面Q,N和點光源(S,w)的透視投影矩陣。
統一的表示
L=(a,b,c,w)=(S,w), a,b,c,w 不同時為零,定義一個矩陣叫做Projection(L,Q,N) 為:$$\begin{bmatrix}
(S-wQ)N^\top I-N^\top S & -wN^\top \\ \\
QN^\top S & SN^\top \\
\end{bmatrix}$$形式上與Perspective(Q,N,S,w) w完全一樣。
w=!0時,L是點光源,其透視投影矩陣是Perspective(Q,N,S,w) w,也就是Projection(L,Q,N)。
現在對於任意的一個給定的S,讓w趨向於0,點光源的位置沿著S方向的直線移動;極限情況下 L是一個與S共線的平行光,lim L = lim (S,w) = (S,0);
而w->0極限情況下 lim Projection(L,Q,N)= Parallel(Q,N,S)SN^T,是一個平行投影矩陣。(求極限都是把w=0帶入)
所以,Projection(L,Q,N)在w!=0時表示點光源的透視投影矩陣,在w=0時表示平行光的平行投影矩陣。
附錄
平行投影
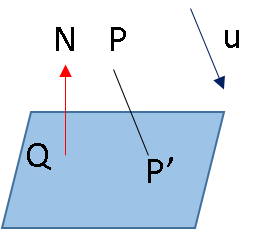
字母既代表 點或(行)向量,也代表它們的座標,運用向量代數: $$\begin{array}{ll}
P' = P+ tu \\
(P'-Q)N^\top = 0\end{array}$$ 解得 \( t = {{QN^\top-PN^\top} \over {uN^\top}} \), 所以 \( P' = P+ \frac{QN^\top u-PN^\top u}{uN^\top} = P + \frac{QN^\top u}{uN^\top} - \frac{PN^\top u}{uN^\top}
=P (I-\frac{N^\top u}{uN^\top}) + \frac{QN^\top}{uN^\top}u \). \( v' = P'-Q = P (I-\frac{N^\top u}{uN^\top}) + Q(\frac{N^\top u}{uN^\top}-I) = (P-Q) (I-\frac{N^\top u}{uN^\top})= v (I-\frac{N^\top u}{uN^\top}) \). 符合仿射變換的定義:P'=PM+w,v'=vM,得: \( M=(I-{N^\top u \over uN^\top}),w={QN^\top \over uN^\top} u \)
透視投影
質點幾何
①把位置是P,質量是m!=0的點記做(mP,m),叫做質點座標。已知某點的質點座標很容易求出它的位置:mP/m=P。 (mP,m)~(P,1),~ 代表等價關係(自反、對稱、傳遞的二元關係),a~b: a b同一位置。②質點座標的好處是質心位置的計算:A(mP,m),B(nQ,n),則A、B的質心為(mP+nQ, m+n) ~ ( (mP+nQ)/(m+n), 1)。
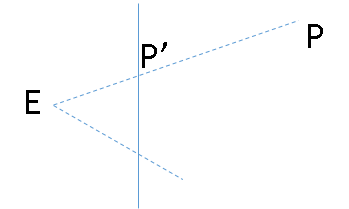
E是投影點,P' 位於投影平面上,該平面過點Q,法向是N(單位法向量),假定方向朝右(朝左不影響的) E到平面的距離=d,P到平面的距離=z, 假設點E的質量=z,點P的質量=d, 則P' 所在的位置恰好是E、P兩點的質心(槓桿EP的支點)。
透視投影矩陣
(E,1)~(Ez,z),(P,1)~(Pd,d),(Ez,z)+(Pd,d) = (Ez+Pd, z+d) ~ (P',1)
其中,\(z=(P-Q)N^\top, \;d=(Q-E)N^\top, \;z+d=(P-E)N^\top \)
所以,\( (Ez+Pd, z+d)=( (P-Q)N^\top E+(Q-E)N^\top P, \; (P-E)N^\top ) \)
\( =( PN^\top E -QN^\top E +(Q-E)N^\top P, \; PN^\top -EN^\top) \)
\( =( P(N^\top E+(Q-E)N^\top I) -QN^\top E, \; PN^\top -EN^\top) \)
假設$$(P,1)\begin{pmatrix}
M & b \\
w & c \\
\end{pmatrix}_{H} =(Ez+Pd, z+d) \sim (P',1) $$
則\( M=N^\top E+(Q-E)N^\top I, \; w=-QN^\top E, \; b= N^\top, c=-EN^\top \)
因為 k (Ez+Pd, z+d)=( k(Ez+Pd), k(z+d) ) ~ (Ez+Pd, z+d) ~ (P',1) k!=0
所以 矩陣H可以 相差非零因子倍,於是法向朝左或朝右沒有關係。