OpenGL ES 透視投影
前面我們知道了一個頂點要想顯示到螢幕上,它的x、y、z分量都要在[-1,1]之間,我們回顧一下渲染管線的圖元裝配階段,它實際上做了以下幾件事:剪裁座標、透視分割、視口變換。圖元裝配的輸入是頂點著色器的輸出,抓喲是物體座標gl_Position,之後到光柵化階段。
圖元裝配
剪裁座標
當頂點著色器寫入一個值到gl_Position時,這個點要求必須在剪裁空間中,即它的x、y、z座標必須在[-w,w]之間,任何這個範圍之外的點都是不可見的。
這裡需要注意以下,對於attribute型別的屬性量。OpenGL會用預設的值替換屬性中未指定的分量,前三個分量會被設定為0,最後一個分量w會被設定為1.
站在gl_position的角度來說,[-w,w]之間的座標點才是可見的,否則都是不可見會被剪裁掉。往前看,在做投影變換的時候我們說,在視景體內的物體有效,視景體外的會被剪裁,實際上是對應的,剪裁就是發生在圖元裝配階段判斷所有的座標是否在[-w,w]之間。
剪裁實際上就是判斷每一個最小三角形、直線、點單元的座標是否規範。
透視除法
對上面的剪裁座標的點的x、y、z座標除以它的w分量,除以w的座標叫做歸一化裝置座標。如果w分量大,除以w後的點就接近(0,0,0),在三維空間中,距離我們較遠的座標如果它的w分量較大,進行透視除法後,就距離原點越近,原點作為遠處物體的消失點,就有三維場景的效果。
視口變換
前面已經使用過視口變換的函式glViewport了,視口是一個而為矩形視窗區域。是OpenGL渲染操作最終顯示的地方。
public static native void glViewport(
int x,
int y,
int w,
int h
);從歸一化裝置座標(x,y,z)到視窗座標(X,Y,Z)的轉換公式
上面公式中的f和n是如下API設定的
public static native void glDepthRangef(
float n,
float f
);n,f指定所需的深度範圍,n,f的取值限於(0.0,1.0)之間,n,f的預設值為0.0和1.0
glDepthRangef函式和glViewport函式指定的值用於將頂點位置從歸一化裝置座標轉換為視窗座標。
利用w分量產生三維效果
在前面的程式碼中,修改傳入的頂點座標,增加w分量
float[] vertexArray = new float[] {
(float) -0.5, (float) -0.5, 0, 1,
(float) 0.5, (float) -0.5, 0, 1,
(float) -0.5, (float) 0.5, 0, 3,
(float) 0.5, (float) 0.5, 0, 3
};同時修改頂點著色器:
private String vertexShaderCode = "uniform mat4 uMVPMatrix;"
+ "attribute vec4 aPosition;"
+ "void main(){"
+ "gl_Position = uMVPMatrix * aPosition;"
+ "}";以及獲取uProjectionMatrix以及傳入頂點資料對應的程式碼,就可以看到如下所示效果
透視投影
然而這樣讓物體產生三維效果的做法太死板了,如果我們還要讓物體平移縮放旋轉,這樣固定的指定w的值就不太好了。
透視投影這個時候就能派上用場了,利用透視投影矩陣自動生成w的值。投影矩陣主要是為w產生正確的值,這樣在渲染管線的後續操作中做透視除法,遠處的物體就看起來比進出物體小,很容易想到,可以利用頂點位置的z分量,將這個距離對映到w分量上,z越大,w也越大。
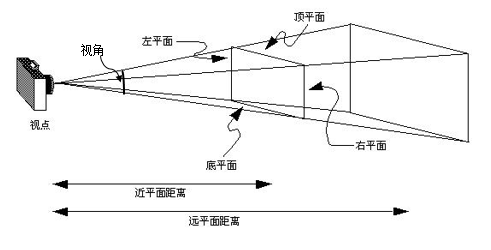
有兩個函式可以生成透視投影矩陣frustumM和perspectiveM。引數具體含義可以參考下面的圖
public static void perspectiveM(float[] m, // 生成的投影矩陣
int offset,
float fovy, // 視角角度
float aspect, // 近平面的寬高比
float zNear, // 近平面
float zFar) // 遠平面frustumM函式原型
public static void frustumM(float[] m, int offset,
float left, float right, float bottom, float top, // 近平面左右下上部與中心點的距離
float near, float far //近平面和元平面與攝像機觀察點的距離
)透視投影背後的數學原理
建立下面的矩陣
a表示視角焦距,焦距等於1/tan(視野/2)
取aspect=1.8,視野45度即a = 1,f = 10,n = 5,得到的透視投影矩陣為
計算下面幾個點
上面這三個點越來越遠,通過透視投影后,z和w都變大了,可以想到,在後面的透視除法時,x和y分量都會變小,於是就會出現距離越遠,匯聚到一個點,也就是三維效果。
同時也可以看到,上面的幾個點他們的z座標都是負值,這也從側面表達了,事實上所有的有效的點z座標必須是負值,也就是從攝像機的座標來看是在z軸負方向,也就是必須在視景體裡面,這一點通過攝像機矩陣來保證。
前面使用正交投影,它的矩陣不會使得w粉量增加,於是通過透視除法也不會使w分量增加,所以正交投影不會出現近大遠小的效果,透視投影會出現近大遠小的效果
透視投影例子
在上面矩形Demo的基礎上修改上面的正方形的頂點資料
float vertices[] = new float[] {
(float) -0.5, (float) -0.5 + + (float)(-0.1*i), (float) (1*i),
(float) 0.5, (float) -0.5 + + (float)(-0.1*i), (float) (1*i),
(float) -0.5, (float) 0.5 + + (float)(-0.1*i), (float) (1*i),
(float) 0.5, (float) 0.5 + + (float)(-0.1*i), (float) (1*i)
};在繪圖時,定義一個數組,傳遞不同的i值,比如繪製四個正方形,這四個正方形的距離越來越遠。
mRectangles = new Rectangle[5];
for (int i = 0; i < mRectangles.length; i++) {
mRectangles[i] = new Rectangle(i);
}在onSurfaceChanged函式裡面設定攝像機位置和透視投影矩陣
Matrix.perspectiveM(mProjectionMatrix, 0, 45, (float)width/height, 2, 15);
Matrix.setLookAtM(mViewMatrix, 0, 0, 0, 12, 0, 0, 0, 0, 1, 0);然後在onDrawFram函式裡面繪製這5個矩形
for (Rectangle rectangle : mRectangles) {
Matrix.setIdentityM(mModuleMatrix, 0);
Matrix.rotateM(mModuleMatrix, 0, xAngle, 1, 0, 0);
Matrix.rotateM(mModuleMatrix, 0, yAngle, 0, 1, 0);
Matrix.multiplyMM(mViewProjectionMatrix, 0, mProjectionMatrix, 0, mViewMatrix, 0);
Matrix.multiplyMM(mMVPMatrix, 0, mViewProjectionMatrix, 0, mModuleMatrix, 0);
rectangle.draw(mMVPMatrix);
}為了呈現出3d效果,增加觸控旋轉事件,這樣滑動螢幕就可以看到三維物體的全貌
public boolean onTouchEvent(MotionEvent e) {
float y = e.getY();
float x = e.getX();
switch (e.getAction()) {
case MotionEvent.ACTION_MOVE:
float dy = y - mPreviousY;
float dx = x - mPreviousX;
mMyRender.yAngle += dx;
mMyRender.xAngle+= dy;
requestRender();
}
mPreviousY = y;
mPreviousX = x;
return true;
}然後就可以看到三維效果。