向量投影與向量投影矩陣
向量投影與向量投影矩陣
向量投影
以下是向量a在向量b上的投影,θ 為兩向量的夾角。

其中a = a||+a⊥,a||則是a在b上的投影。 θ
![]()
![]()
所以投影公式如下:
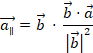
向量投影矩陣
將以上投影公式寫成矩陣形式,這裡使用的是列優先的矩陣,即向量寫成一列多行。
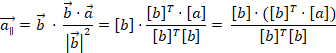
因為矩陣相乘符和結合律,所以:
![]()
![]() 是一個矩陣,如果是二維向量則是2*2的矩陣,如果是三維向量則是一個3*3的矩陣,這個也就是向量投影矩陣。
是一個矩陣,如果是二維向量則是2*2的矩陣,如果是三維向量則是一個3*3的矩陣,這個也就是向量投影矩陣。
將向量投影矩陣記作P,則:
![]()
P矩陣有些特性,首先P矩陣是一個對稱矩陣,所以轉置矩陣PT = P。其次如果一個向量在另一個向量上進行多次投影,其結果相等的,所以P^2 = P
也就有 PT = P = P^2 = P^3 = … = P^n
參考:
https://blog.csdn.net/williamgavin/article/details/77427164
《3D數學基礎:圖形與遊戲開發》—— 5.10.3
相關推薦
向量投影與向量投影矩陣
向量投影與向量投影矩陣 向量投影 以下是向量a在向量b上的投影,θ 為兩向量的夾角。 其中a = a||+a⊥,a||則是a在b上的投影。 θ 所以投影公式如下: 向量投影矩陣 將以上投
平行投影與透視投影的關係與統一的矩陣表示
D3DXMatrixShadow 產生一個矩陣,把幾何體投影到平面上,神奇的是這個矩陣不論對平行光還是點光,都具有統一的形式(見左邊D3DXMatrixShadow的文件連結)。 Introduction to 3D Game Programming with Direct
OpenCV 實現圖片的水平投影與垂直投影,並進行行分割
對於印刷體圖片來說,進行水平投影和垂直投影可以很快的進行分割,本文就在OpenCV中如何進行水平投影和垂直投影通過程式碼進行說明。水平投影:二維影象在y軸上的投影垂直投影:二維影象在x軸上的投影由於投影的影象需要進行二值化,本文采用積分二值化的方式,對圖片進行處理。具體程式碼
使用OpenCv中Mat進行水平投影與垂直投影並實現字元切分
因為要做影象處理方面的工作,所以最近在學習OpenCv的使用,學習了OpenCv中Mat物件的相關使用之後,實現了使用Mat物件來進行影象的水平投影和垂直投影,並且在投影之後,對字元進行相對應的切分。現在將相關程式碼貼出,一來可以供大家參考並指正錯誤,而來也為的是防止忘記了
Android開發筆記(一百三十二)向量圖形與向量動畫
向量圖形VectorDrawable 與水波圖形RippleDrawable一樣,向量圖形VectorDrawable也是Android5.0之後新增的圖形類。向量圖不同於一般的圖形,它是由一系列幾何曲線構成的影象,這些曲線以數學上定義的座標點連線而成。具體到實現上,則需開
矩陣等價 與 向量組 等價
這也是考試喜歡考察的一塊地方,注意它們之間的區別 (1)矩陣等價AB 這是指經過A經過有限次初等變換可以化為B。兩矩陣等價的前提條件是同型。 判別條件r(A)=r(B) 即兩矩陣等價的充要條件是矩陣同型且秩相同。 (2)向量組等價 這就不需要有同型的條件 必要條件:r(I
線性代數(六)矩陣的特徵值與特徵向量——特徵值與特徵向量求解 矩陣對角化
本節主要知識點 1.特徵向量與特徵值的定義:A為n階方陣,x為非零向量,Ax=λx,則λ為A的特徵值,x為A的屬於特徵值的特徵向量。 2.特徵值與特徵向量的求解過程(重點) 寫出f(λ)=det(A-λI) 特徵值:計算f(λ)的全部根 特徵向量:對A的每一個特徵值
矩陣2範數與向量2範數的關係
向量2範數是對應元素平方和:矩陣2範數是:其中是矩陣的最大特徵值. 除此之外,矩陣有一個F範數(Frobenius範數)倒是跟向量的2範數比較相似,是矩陣內所有元素平方和: 矩陣的2範數是向量二範數對應的誘導範數。給定某一種向量範數 ,它所對應的矩陣範數定義為: 左邊的範數
OpenCV計算變換與重投影的矩陣說明
本篇部落格主要討論opencv中兩個函式中幾何變換(矩陣)的對應關係,以下函式介面摘自opencv-2.4.8官方文件 1.Finds an object pose from 3D-2D point correspondences. bool solve
機器學習:向量空間中的投影
今天介紹向量空間中的投影,以及投影矩陣。 假設空間中有兩個向量 a,b\mathbf{a}, \mathbf{b}a,b,b\mathbf{b}b 在 a\mathbf{a}a 上的投影為 p\mathbf{p}p,我們要計算出 p\mathbf{p}p 到底是
求向量a在向量b上的投影
求向量a={4,-3,4}在向量b={2,2,1}上的投影。 a在b上的投影等於|a|乘以ab夾角的餘弦,然後再乘以b的單位向量即可! 因此等於|a| * a.b /|a||b| * b/|b|
地圖投影和向量瓦片詳解
一.引言 地圖投影的分類很多,世界上目前主流地圖都是採用的Web墨卡託投影方式(國際組織稱其為3857或900913投影),國內高德和百度地圖也是採用的Web墨卡託的投影方式,除了Web墨卡託之外,經緯度投影(簡稱4326投影)也是比較常用,向量
求和向量與中心化矩陣
symbol 元素 mmu 公式 之間 bold 標量 erl 數據 一、求和向量 所有元素等於1 的向量稱為求和向量(summuing vector)。記為$\mathbf{1}=[1,1, \cdots, 1]^{\mathbf{T}}$ 。以$n=4$為例,求和向量
數學 - 線性代數 - #12 向量空間的衍生:矩陣空間、微分方程的解、圖
對象 矩陣 mar nodes all 向量 cnblogs 導論 概念 線性代數導論-#12 向量空間的衍生:矩陣空間、微分方程的解、圖 凡是可以進行加法和數乘運算的對象,我們都可以將其視為向量。 凡是對加法和數乘封閉的集合,我們都可以將其視為空間。 分析空間時,我們著
線性可分支持向量機與軟間隔最大化
技術分享 最大化 bubuko 線性 分支 inf http bsp 9.png 線性可分支持向量機與軟間隔最大化
Silverlight & Blend動畫設計系列十:Silverlight中的坐標系統(Coordinate System)與向量(Vector)運動
過度 highlight 圖片 nbsp mgr ack jpg .com bsp 原文:Silverlight & Blend動畫設計系列十:Silverlight中的坐標系統(Coordinate System)與向量(Vector)運動 如果我們習慣於數學坐
向量空間與線性子空間
向量空間是線性代數研究的基本物件,它是一個集合。在該集合內,可以做向量的加法(兩個向量相加仍然在該集合中),向量與標量的乘法,並且改加法與乘法還滿足八個公理。具體可參見維基百科:https://en.wikipedia.org/wiki/Vector_space 注:齊次線性方程組的
向量點乘與向量叉乘的意義
今天學習OpenGL的時候,看到教程上面光照部分關於向量乘積之間的的程式碼,由於之前沒有好好學習數學,所以感到十分的懵逼,在網上看了一個部落格之後感到豁然開朗。這是部落格原文:向量點乘與叉乘的幾何意義。我主要是為了方便自已以後新增和查詢。 向量的點積公式為:a * b = |a| * |b| *
【VTK】vtk actor空間變換後的點對映與向量對映
在三維空間中,人們通常需要對平面等形體進行旋轉,拖拽等操作。比如下面的過程: 將平面繞平面的Y軸旋轉一定角度 將其繞平面自身的X軸旋轉一定角度 將平面向向量方向(1, 2, 3)移動一段距離。 這樣複雜的操作通常需要我們使用vtkActo
詳解SVM系列(三):線性可分支援向量機與硬間隔最大化
支援向量機概覽(support vector machines SVM) 支援向量機是一種二類分類模型。它的基本模型是定義在特徵空間上的間隔最大(間隔最大區別於感知機)線性分類器(核函式可以用非線性的分類)。 支援向量機的學習策略是間隔最大化可形式化為一個求解凸二次規劃的問題。 也等
