動態規劃之切割繩子
阿新 • • 發佈:2019-01-08
/*
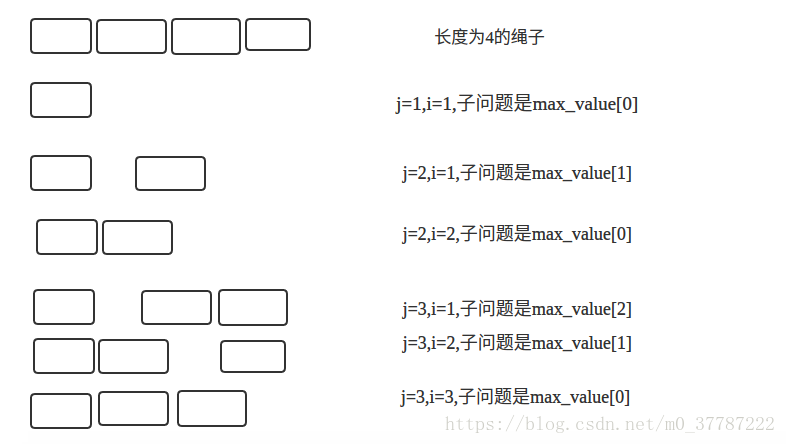
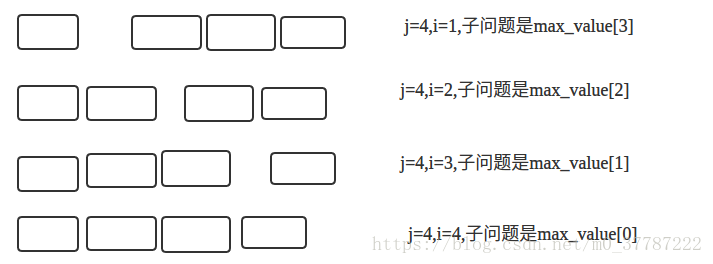
切割繩子,每段繩子都有一個最大值,給定長度為n的繩子,如何切割讓利益最大化
自底而上的方法,對於任何子問題,直至它依賴的所有子問題都解決,才會去解決它。
*/
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
vector<int> max_value(100,0);//當長度為n時,最大利益
vector<int> first_cut(100,0);//當長度為n時,切割一刀的位置
vector<int> price{0,1 每個子問題說白了就是上一次求解的所有子問題的和