連結：http://hihocoder.com/problemset/problem/1069
思想：
利用dfs + ST 演算法
記錄下dfs的序列，還有dfs過程中每一個點的深度，對應到之前的dfs的序列中。還需要記錄一個在dfs中每一個節點首次出現的位置，也是對應到dfs的那個序列中。
舉個例子（畫的很醜）

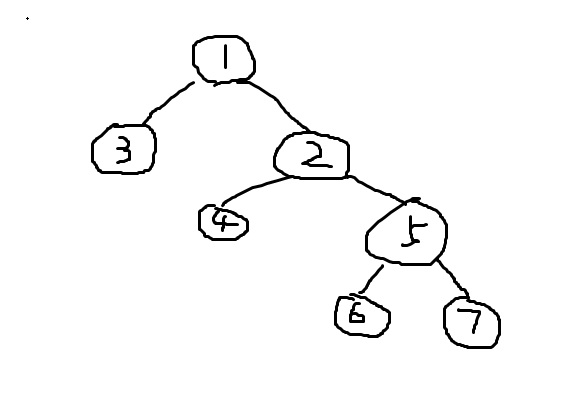
假設先去右兒子這樣可以得到
dfs序列稱作f : 1 2 5 7 5 6 5 2 4 2 1 3 1
深度序列稱作dep: 1 2 3 4 3 4 3 2 3 2 1 2 1
首次出現序列稱作first : 1 2 12 9 3 6 4

對於查詢兩個點之間的LCA就是各自第一次出現的路徑之間一個深度最小的點。
這裡就出現一個RMQ問題，在一段序列之中查詢一個最小的值，所以運用了ST演算法來解決這個問題
LCA(4,5) = RMQ(dep,first[4],first[7]) 將4和7的LCA 轉換成求4 到 7 第一次出現的之間的序列的深度最小的值。
first[4] = 9 ,first[7] = 4 就是要求 4 3 4 3 2 3 這個序列的深度最小值， 是深度為2，對應到dfs的序列中是在第8個，返回f[8] 得到 節點 2 。
這裡就是要求出的是最小值的index，然後利用這個index 在 dfs序列中對應到節點編號
程式碼:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <map>
using namespace std;
#define M 500009
int dep[M],pos[M],f[M];
int in[M];
int dp[M][100];
vector<int> adj[M];
map
 
<string,int> mp;
string name[M];
int n,m;
int tot;
void init()
{
    tot = 0;
    mp.clear();
    memset(in,0,sizeof(in));
    memset(dp,0,sizeof(dp));
    for(int i = 0;i <= n;i++) adj[i].clear();
}
void dfs(int u,int pre,int depth)
{
    f[++tot] = u; //dfs array which record the order
    pos[u] = tot; //record the first time when a node is visited.the index mean the number of the node
 

    dep[tot] = depth; // record the depth
    for(int i = 0;i < adj[u].size();i++)
    {
        int v = adj[u][i];
        if(v == pre) continue;
        dfs(v,u,depth+1);
        f[++tot] = u; // it can't be the first time,so the pos array isn't needed
        dep[tot] = depth;
    }
}
void st()
{
    for(int i = 1;i <= tot;i++)
        dp[i][0] = i; // dp[i][j] record the index of the RMQ from i to i + 2^j - 1
    for(int j = 1;(1<<j) <= tot;j++)
    {
        for(int i = 1;i + (1<<j) - 1 <= tot;i++)
        {
            int mid = i + (1<<(j-1));
            if(dep[dp[i][j-1]] < dep[dp[mid][j-1]]) dp[i][j] = dp[i][j-1];
            else dp[i][j] = dp[mid][j-1];
        }
    }
}
int rmq(int l,int r)
{
    l = pos[l];
    r = pos[r];
    if(l > r) swap(l,r);
    int len = r - l + 1;
    int k = (int)(log((double)len) / log(2.0));
    if(dep[dp[l][k]] < dep[dp[r-(1<<k)+1][k]]) return dp[l][k];
    return dp[r-(1<<k)+1][k];
}
int main()
{
    //freopen("in.txt","r",stdin);
    while(cin >> n)
    {
        init();
        for(int i = 0;i < n;i++)
        {
            string a,b;
            cin >> a >> b;
            if(mp[a] == 0)
            {
                mp[a] = ++tot;
                name[tot] = a;
            }
            if(mp[b] == 0)
            {
                mp[b] = ++tot;
                name[tot] = b;
            }
            adj[mp[a]].push_back(mp[b]); // input the tree
            in[mp[b]]++;
        }
        tot = 0;
        for(int i = 1;i <= n;i++)
        {
            if(in[i] == 0)
            {
                dfs(i,-1,0);
                break;
            }
        }
        st();
        cin >> m;
        while(m--)
        {
            string a,b;
            cin >> a >> b;
            int aa = mp[a],bb = mp[b];
            int ans = rmq(aa,bb); // ans is the index of the minimum in (aa,bb) of dep
            cout << name[f[ans]] << endl;
        }
    }
    return 0;
}