橢圓曲線加密學習的菜鳥入門
阿新 • • 發佈:2019-01-09
橢圓曲線:一個更好的trapdoor構件
橢圓曲線是滿足特定數學等式的點的集合。橢圓曲線的方程像如下的樣子:

它的影象:
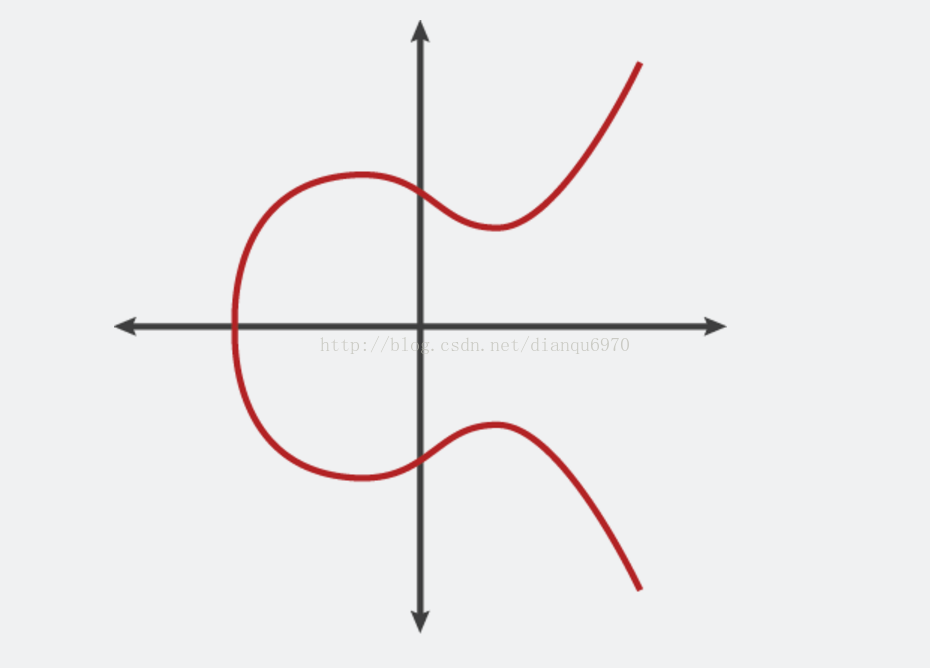
還有其他形式的橢圓曲線的表達形式,但是一般的橢圓曲線方程,一個變數為2階,一個變數為3階。它有一些好的屬性用於加密。
1.奇怪的對稱性
它是水平對稱的。圖形是關於x軸對稱的。
更有趣的是,任何不垂直的直線最多與曲線有三個交點。
讓我們把這個曲線想象成一個奇異的桌球遊戲。在曲線上任取兩個點,並畫一條線進過他們,這個直線將再穿過曲線至多一個點。在這個桌球遊戲中,拿一個球從A點射向B點,當它擊中曲線時,這個球要麼筆直向上彈(在x軸的下面)或者筆直向下彈(在x軸的上方),彈向曲線的另一邊。
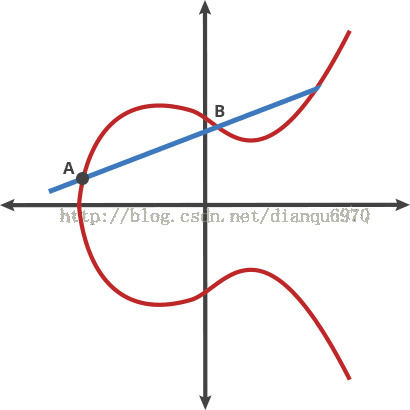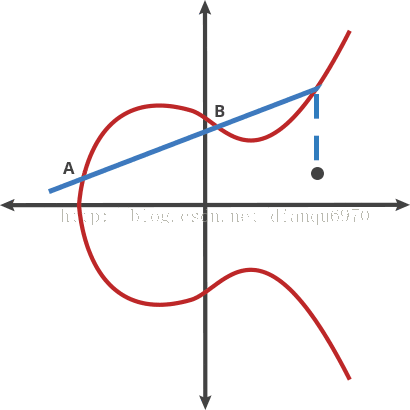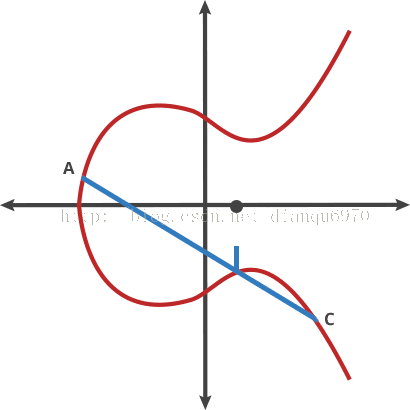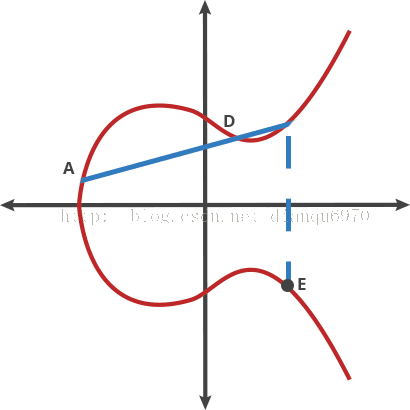
我們稱這個經過兩點的桌球叫“打點”。任何兩個點通過打點可以得到一個新的點。
A dot B=C
我們可以反覆這個規則:
A dot A=B
A dot B=C
A dot C=D
…
橢圓曲線是滿足特定數學等式的點的集合。橢圓曲線的方程像如下的樣子:

它的影象:

還有其他形式的橢圓曲線的表達形式,但是一般的橢圓曲線方程,一個變數為2階,一個變數為3階。它有一些好的屬性用於加密。
1.奇怪的對稱性
它是水平對稱的。圖形是關於x軸對稱的。
更有趣的是,任何不垂直的直線最多與曲線有三個交點。
讓我們把這個曲線想象成一個奇異的桌球遊戲。在曲線上任取兩個點,並畫一條線進過他們,這個直線將再穿過曲線至多一個點。在這個桌球遊戲中,拿一個球從A點射向B點,當它擊中曲線時,這個球要麼筆直向上彈(在x軸的下面)或者筆直向下彈(在x軸的上方),彈向曲線的另一邊。

我們稱這個經過兩點的桌球叫“打點”。任何兩個點通過打點可以得到一個新的點。
A dot B=C
我們可以反覆這個規則:
A dot A=B
A dot B=C
A dot C=D
…
這說明了如果你有兩個點,經過n次的打點之後將得到一個最終的點。僅僅知道原始點和最終點來找出n是很難的。為了繼續拿這個桌球遊戲來暗喻,一個人在隨機的時間段內按照桌球的規則進行著這個遊戲,這是很簡單的。但是,如果另一個人在開始後的某段時間進入後,即使他看見了球終止的地方,和球起始的點,他也很難決定打點的次數,除非他全程在看著這個遊戲。容易做,卻很難解,這個是trapdoor函式的基礎。
上述就是基於橢圓加密的一個基本的思想。
